OFDM载波间隔_LTE子载波间隔与符号持续时长关系

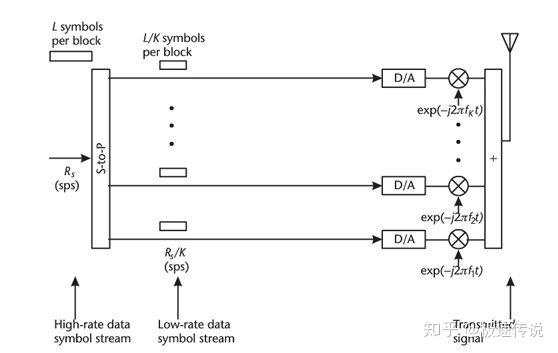
图是一张典型的FDM原理图。在输入端有一串高速基带数据流，假设速率是100M 符号/秒，那么每个基带符号的持续时间是0.01微秒。假设串并转换器可以将串行数据流转换成10路并行低速数据流，这意味着系统可以一次处理10个基带符号。10个基带符号的持续时间是0.1微秒，这意味着每个低速数据流的速率是10M 符号/秒，即低速数据流上每个符号的持续时间是基带符号的10倍，即0.1微秒。然后，每个低速数据符号被调制到一个子载波。经过模数转换后汇合成一个复杂的包含了10个频域信号的FDM符号，被发送到空口。这个复杂的FDM符号的持续时间是0.1微秒。

上面的例子用到了10个子载波。如果使用20个子载波，相对于固定的系统带宽来说，子载波间隔就变小了。这时，串并转换器可以将串行数据流转换成20路并行低速数据流，这意味着系统可以一次处理20个基带符号。20个基带符号的持续时间是0.2微秒，这意味着每个低速数据流的速率是5M 符号/秒，即低速数据流上每个符号的持续时间是基带符号的20倍，即0.2微秒。然后，每个低速数据符号被调制到一个子载波。经过模数转换后汇合成一个复杂的包含了10个频域信号的FDM符号，被发送到空口。这个复杂的FDM符号的持续时间是0.2微秒。

由此可见，子载波间隔越大，子载波数量越少，FDM符号的持续时间就越短。

对于OFDM，只要把上图略作修改，增加一个IDFT，同样可以得到“子载波间隔越大，子载波数量越少，OFDM符号的持续时间就越短”的结论。

那么，5G NR的各个numerology中，各个OFDM持续时间分别是多长呢？

根据3GPP TS 38.211的定义，不管什么numerology，每个时隙中都是14个OFDM符号（还是与LTE有区别：LTE的每个时隙是7个OFDM符号，而每个子帧是14个OFDM符号）。如果子载波间隔是15KHz，那么时隙长度是1ms；如果子载波间隔是30KHz，那么时隙长度是0.5ms；如果子载波间隔是60KHz，那么时隙长度是0.25ms；如果子载波间隔是120KHz，那么时隙长度是0.125ms；如果子载波间隔是240KHz，那么时隙长度是0.0625ms。这样的设计正利用了“子载波间隔越大，OFDM符号的持续时间就越短”的属性。