Numpy中np.random.rand()和np.random.randn()用法和区别详解

numpy.random.rand(d0, d1, …, dn)的随机样本位于[0, 1)中：本函数可以返回一个或一组服从**“0~1”均匀分布**的随机样本值。

numpy.random.randn(d0, d1, …, dn)是从标准正态分布中返回一个或多个样本值。

 1. np.random.rand()

语法：

np.random.rand(d0,d1,d2……dn)
注：使用方法与np.random.randn()函数相同

作用：
通过本函数可以返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)，不包括1。

应用：在深度学习的Dropout正则化方法中，可以用于生成dropout随机向量（dl），
例如（keep_prob表示保留神经元的比例）：

dl = np.random.rand(al.shape[0],al.shape[1]) 

举例：

注：

均匀分布:

也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。

均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为U（a，b）。

均匀分布的概率密度函数为：

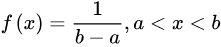
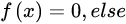
2. np.random.randn() 语法：

np.random.randn(d0,d1,d2……dn)
1)当函数括号内没有参数时，则返回一个浮点数；
2）当函数括号内有一个参数时，则返回秩为1的数组，不能表示向量和矩阵；
3）当函数括号内有两个及以上参数时，则返回对应维度的数组，能表示向量或矩阵；
4）np.random.standard_normal（）函数与np.random.randn()类似，但是np.random.standard_normal（）的输入参数为元组（tuple）。

# 举例：
np.random.standard_normal((5))
# [-0.53268495 0.30171848 1.85232368 -0.58746393 0.19683992]

np.random.standard_normal((5,2))
""" 
[[-2.44520524 2.29767001]
 [-1.19770033 -1.09569325]
 [-0.75414833 0.49509984]
 [-1.42537268 0.41788237]
 [ 1.85465491 -1.44383249]] 
 """
 
np.random.standard_normal((5,2,3))
"""
[[[ 0.54013502 -0.25347615 1.73395647]
 [ 1.03386947 -0.54856199 2.10004584]]

 [[-0.57632903 -0.05856844 1.72805595]
 [ 1.3507174  0.61459539 0.63380028]]

 [[-2.24857933 -1.29276097 0.42585061]
 [ 0.75974263 -0.83670586 -1.56930898]]

 [[-0.32212   1.2884624  1.53744081]
 [ 1.5444555 -1.82408734 -0.55952688]]

 [[-1.21191144 -1.40454518 -0.3369976 ]
 [-0.89314143 0.28291988 1.58394166]]]
"""

np.random.standard_normal((5,2,3,1))
"""
[[[[ 0.19019221]
  [ 0.64618425]
  [ 0.99815722]]

 [[-0.0570328 ]
  [ 0.83271045]
  [-0.30469335]]]


 [[[-1.14788388]
  [ 0.09563431]
  [ 2.05611213]]

 [[-0.14251287]
  [ 1.00922816]
  [-0.55403104]]]


 [[[ 1.75657437]
  [ 1.46381575]
  [ 1.10527197]]

 [[ 0.22667296]
  [ 0.18305552]
  [ 0.5778761 ]]]


 [[[ 0.26501242]
  [-0.4863313 ]
  [ 1.01096974]]

 [[-2.46562874]
  [ 0.19516242]
  [-1.92500848]]]


 [[[ 0.97904566]
  [ 0.80444414]
  [ 0.99981326]]

 [[-0.74329878]
  [-0.9265738 ]
  [ 0.0288684 ]]]]
  """

5）np.random.randn()的输入通常为整数，但是如果为浮点数，则会自动直接截断转换为整数。

作用：通过本函数可以返回一个或一组服从标准正态分布的随机样本值。

特点： 标准正态分布是以0为均数、以1为标准差的正态分布，记为N（0，1）。对应的正态分布曲线如下所示，即：

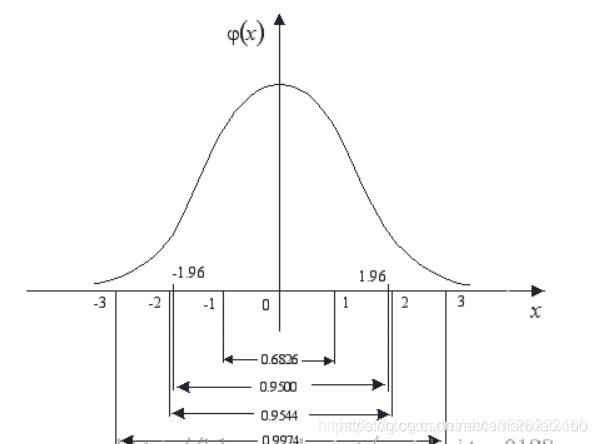
注：

标准正态分布曲线下面积分布规律是：

在-1.96～+1.96范围内曲线下的面积等于0.9500（即取值在这个范围的概率为95%），在-2.58～+2.58范围内曲线下面积为0.9900（即取值在这个范围的概率为99%）.
因此，由 np.random.randn()函数所产生的随机样本基本上取值主要在-1.96~+1.96之间，当然也不排除存在较大值的情形，只是概率较小而已。

参考：

https://blog.csdn.net/abc13526222160/article/details/86423754

https://www.cnblogs.com/BBS2013/p/12839042.html

到此这篇关于Numpy中np.random.rand()和np.random.randn() 用法和区别详解的文章就介绍到这了,更多相关Numpy np.random.rand()和np.random.randn()内容请搜索编程笔记以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程笔记！

原文链接：https://blog.csdn.net/lemonxiaoxiao/article/details/109205647