牛B三人组快速排序堆排序归并排序

快速排序

• 随便取个数&＃xff0c;作为标志值&＃xff0c;这里就默认为索引位置为0的值
• 记录左索引和右索引&＃xff0c;从右往左找比标志值小的&＃xff0c;小值和左索引值交换&＃xff0c;右索引变化&＃xff0c;然后从左往右找比标志值大的&＃xff0c;大值和右索引值交换&＃xff0c;左索引变化
• 循环第二步骤直到左索引和右索引碰头&＃xff0c;标志值和当期左索引(右)交换&＃xff0c;这样一个循环下&＃xff0c;就得出一个标志值左边都比它小&＃xff0c;右边都比大的数据样本
• 利用递归&＃xff0c;对数据进行上述过程的最终标志值索引分割&＃xff0c;分割到递归底层只有两个数&＃xff0c;那么上述过程排序就一定有序了

　　实现要点&＃xff1a;随机取标志值&＃xff0c;循环右取小、左取大&＃xff0c;利用左右索引碰头位置进行递归分割

 　　快速排序一般情况很快&＃xff0c;但是遇到最坏情况(倒序的情况)&＃xff0c;算法复杂度为O(n2),最好的情况(正序),算法复杂度为O(n)

　　快速排序有可能超过最大递归深度 

堆排序

　　堆排序难点就是有一堆的概念需要你理解&＃xff0c;开始前&＃xff0c;那就必须讲讲概念了

　　树结构&＃xff1a;我们程序见到的结构很像生活中的树&＃xff0c;不过这里的是倒挂的&＃xff0c;根在上&＃xff0c;叶子在下&＃xff0c;而根&＃xff0c;在结构中&＃xff0c;我们称为根节点&＃xff0c;叶子称为叶子节点&＃xff0c;中间的为枝节点

　　满二叉树和完全二叉树&＃xff1a;

• 二叉树&＃xff0c;就是每个节点最多两个枝节点或叶子节点
• 深度k&＃xff0c;数下树有多少层&＃xff0c;比如下图就是深度为4

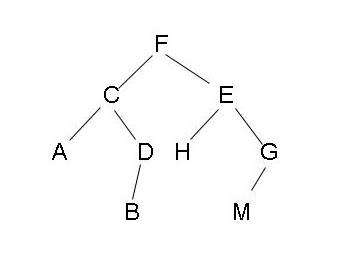
• 满二叉树&＃xff0c;除最后一层叶子节点&＃xff0c;其他层节点都有两个子节点&＃xff0c;节点数满足2^k-1

• 完全二叉树&＃xff0c;节点数满足至少有2k-1个&＃xff0c;至多有2k-1个&＃xff0c;最后一层叶子节点可缺&＃xff0c;但是这个缺&＃xff0c;要连续缺&＃xff0c;比如上图&＃xff0c;缺7或缺67或缺567

　　大根堆和小根堆&＃xff1a;

• 大根堆&＃xff1a;满足父节点都比子节点大的完全二叉树

• 小根堆&＃xff1a;满足父节点都比子节点小的完全二叉树

　　树的存储&＃xff1a;存储时&＃xff0c;我们用的就是列表存储&＃xff0c;不过你会想&＃xff0c;那怎么体现树的结构在里面的呢&＃xff1f;从根节点开始&＃xff0c;根节点放入索引位置为0的地方&＃xff0c;下一层&＃xff0c;从左为右依次放入&＃xff0c;就如下图

　　树的存储规律&＃xff1a;

• 已知父节点位置为i&＃xff0c;获取左子节点位置为&＃xff1a;2i&＃43;1&＃xff0c;获取右子节点位置为&＃xff1a;2i&＃43;2
• 已知子节点位置为i&＃xff0c;获取父节点&＃xff1a;无论这个子节点是左子还是右子&＃xff0c;(i-1) // 2

　　堆的向下调整和建堆

　　由于刚开始拿到堆并不满足大根堆(大根堆用于从小到大排序&＃xff0c;因为每次取完根节点最大数都是放在树的最后位置&＃xff0c;也就是列表的最后位置&＃xff0c;小根堆则用于从大到小排序)的情况&＃xff0c;所以还需要了解堆的向下调整和建堆

• 堆的向下调整&＃xff0c;如下图&＃xff0c;刚开始堆不满足大根堆&＃xff0c;因为不满足根节点30比47,91大&＃xff0c;所以需要进行向下调整&＃xff0c;第一步&＃xff1a;左右子节点比较&＃xff0c;91大&＃xff0c;并且大于根节点&＃xff0c;发生位置交换    第二步&＃xff1a;30下一层左右子节点比较&＃xff0c;85大&＃xff0c;也比30大&＃xff0c;发生位置交换

　　经过上面过程&＃xff0c;此时的堆就是大根堆了&＃xff0c;不过这个调整过程有个前提&＃xff0c;就是根节点下的子堆已经满足大根堆的条件&＃xff0c;建立这个条件&＃xff0c;我们叫建堆

• 建堆&＃xff1a;过程就要从底层的堆开&＃xff0c;好比民主选择样&＃xff0c;先从村选村长&＃xff0c;再从村长中选县长&＃xff0c;层层推举上去&＃xff0c;如下图

　　第一步&＃xff1a;85-91堆选举&＃xff0c;91大&＃xff0c;当村长&＃xff0c;91目前就是村长&＃xff0c;不用换

　　第二步&＃xff1a;12-24-30堆选举&＃xff0c;30大&＃xff0c;当县长&＃xff0c;情况满足不用换

　　第三步&＃xff1a;85-47-91-36堆选举&＃xff0c;91大&＃xff0c;当县长&＃xff0c;36-91交换&＃xff0c;而且36比85小&＃xff0c;村长也当不了&＃xff0c;85-36交换&＃xff0c;该过程就是向下调整的过程&＃xff0c;村级对满足大根堆条件

　　第四步&＃xff1a;整个堆推选市长&＃xff0c;53小&＃xff0c;又是向下调整的过程

　　所以建堆本质上也就是小堆基础上进行向下调整就能达到建堆的目的

　　代码实现要点&＃xff1a;

• 堆向下调整&＃xff1a;堆调整的上下边界&＃xff0c;循环过程从2i&＃43;1左子节点开始&＃xff0c;左右(前提是有右子)子节点比较大小-然后和父节点值比较确定是否交换
• 建堆&＃xff1a;确定最后叶子节点(n-1)的父节点((n-2) // 2), 倒序循环调用向下调整
• 取数&＃xff1a;根节点数与最后位置发生交换&＃xff0c;调用向下调整(注意下边界high的变化&＃xff0c;排除取好的最大数在调整范围)

　　利用堆排序解决topK问题

　　思路&＃xff1a;需要多少k&＃xff0c;就建立以k个节点的小根堆&＃xff0c;循环剩下数&＃xff0c;如果比当前堆的根节点大&＃xff0c;放入堆中&＃xff0c;进行向下调整

归并排序

　　归并排序的原理是两个已经有序的列表合并为大的有序列表&＃xff0c;合并过程中&＃xff0c;两个列表各自最小的数进行比较&＃xff0c;把小的放入到一个新的列表

　　归并排序分为两个过程&＃xff1a;拆分过程和合并过程&＃xff0c;拆分过程好弄&＃xff0c;就按一半一半的拆&＃xff0c;直到底层为一个数的列表&＃xff0c;此时开始合并&＃xff0c;此时合并的前提--两个有序的列表已经满足

　　代码实现点&＃xff1a;利用递归一半一半的分&＃xff0c;合并&＃xff1a;确定两个列表的边界范围&＃xff0c;两个各取最小数进行比较-小的添加到新列表-对应的索引变化

　　注意&＃xff1a;肯定有一边的数因为普遍小&＃xff0c;先循环完&＃xff0c;所以最后只要还有数的列表进行循环添加就可以了