密码库LibTomCrypt学习记录——（2.29）分组密码算法的工作模式——KeyWrap密钥封装模式

1. 密钥封装(Key Wrap)

密钥封装是为了对密钥进行保护&＃xff0c;比如密钥存储在不太安全的存储设备中&＃xff0c;或者密钥需要在网络中传输。

早在2001年&＃xff0c;NIST就发布了AES Key Wrap Specification。2002年&＃xff0c;IETF在RFC 3394中也描述了密钥封装算法AES-KeyWrap Algorithm&＃xff0c;电信行业协会发布了使用TDES的密钥封装算法。2008年&＃xff0c;美国标准认可委员会&＃xff08;Accredited Standards Committee X9, Inc.&＃xff09;发布了金融服务业的密钥封装算法。2009年&＃xff0c;RFC 5649 描述了带填充的密钥封装算法。 2012年&＃xff0c;NIST SP 800-38F描述了AES KW、AES KWP&＃xff08;带填充的密钥封装算法&＃xff09;和TDES的TKW。

NIST的这三个算法和RFC等的描述几乎完全一致。

     以下描述以NIST SP 800-38F为主&＃xff0c;结合RFC 3394和RFC 5649。

     参考文献

1. Key Wrap - Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/Key_Wrap
2. NIST Special Publication 800-38F: Recommendation for Block Cipher Modes of Operation Methods for Key Wrapping, December 2012.
3. J. Schaad and R. Housley, Advanced Encryption Standard (AES) Key Wrap Algorithm, RFC 3394, September, 2002.
4. R. Housley and M. Dworkin, Advanced Encryption Standard (AES) Key Wrap with Padding Algorithm, RFC 5649, August, 2009.
5. ANSI/TIA-102.AACA-1-2002: Project 25 – Digital Radio Over-the-Air-Rekeying (OTAR) Protocol: Addendum 1 – Key Management Security Requirements for Type 3 Block Encryption Algorithms, Telecommunications Industry Association, November, 2002.
6. ANS X9.102-2008, Symmetric Key Cryptography For the Financial Services Industry—Wrapping of Keys and Associated Data, Accredited Standards Committee X9, Inc., June, 2008.

1. 密钥封装有三种

1. KW          基于AES的密钥封装&＃xff0c;不使用填充。
2. KWP   基于AES的密钥封装&＃xff0c;使用填充。
3. TKW   基于TDES的密钥封装&＃xff0c;不使用填充。

1. W

C &＃61; W(S)模块

准备&＃xff1a;

1. K(即KEK)
2. 128-bit 分组密码CIPH.

输入&＃xff1a;

1. S&＃xff0c;长度为n×64bit&＃xff0c;n ≥ 3.

输出

1. C&＃xff0c;与S等长&＃xff08;长度为n×64bit&＃xff0c;n ≥ 3&＃xff09;。

步骤

1. 初始化

s &＃61; 6(n-1).

S&＃61;S1 || S2 ||… || Sn . Si都是64it

A0 &＃61; S1.

For i &＃61; 2, …, n

R0i &＃61; Si.

2. 迭代

For t &＃61; 1, …, s

          At &＃61; MSB64(CIPHK(At-1 || R2t-1)) ⊕ [t]64;

          For i &＃61; 2, …, n-1:

Rit &＃61; Ri&＃43;1t-1;

          Rnt &＃61; LSB64(CIPHK (At-1 || R2t-1)).

3. 输出结果

C1 &＃61; As.

For i &＃61; 2, …, n

Ci &＃61; Ris.

Return C1 || C2 || … || Cn.

W的示意图如下

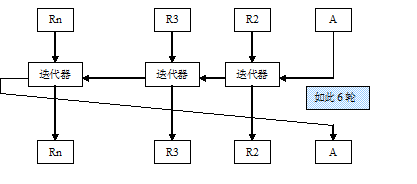
W的示意图

W中迭代器的示意图如下&＃xff1a;

W中迭代器的示意图

1. W-1

S &＃61; W-1(C)模块

准备&＃xff1a;

1. K(即KEK)
2. 128-bit 分组密码CIPH的逆函数CIPH-1

输入&＃xff1a;

1. C&＃xff0c;长度为n×64bit&＃xff0c;n ≥ 3.

输出

1. S&＃xff0c;与c等长&＃xff08;长度为n×64bit&＃xff0c;n ≥ 3&＃xff09;。

步骤

1. 初始化

s &＃61; 6(n-1).

C &＃61; C1 || C2 ||… || Cn . Ci都是64bit

As &＃61; C1.

For i &＃61; 2, …, n

Rsi &＃61; Ci.

2. 迭代

For t &＃61; s, …, 1

          At-1 &＃61; MSB64((CIPH-1K(At ⊕[t]64)) || Rnt);

R2t-1 &＃61; LSB64(CIPH-1K ((At ⊕[t]64) || Rnt).

          For i &＃61; 2, …, n-1:

Ri&＃43;1t-1 &＃61; Rit ; 

3. 输出结果

S1 &＃61; A0.

For i &＃61; 2, …, n

Si &＃61; Ri0.

Return S1 || S2 || … || Sn.

1. KW

KW的加密KW-AE(P)和解密KW-AD(C)。

加密C &＃61; KW-AE(P)

输入&＃xff1a;明文P

输出&＃xff1a;密文C

1. ICV1 &＃61; 0xA6A6A6A6A6A6A6A6.

2. S &＃61; ICV1 || P.

3. Return C &＃61; W(S).

解密P &＃61; KW-AD(C)

输入&＃xff1a;密文C

输出&＃xff1a;明文P或者失败

1. ICV1 &＃61; 0xA6A6A6A6A6A6A6A6.

2. S &＃61; W-1(C).

3. If MSB64(S) ≠ICV1, return FAIL and stop.

4. Return P &＃61; LSB64(n-1)(S).

RFC 3394对KW采用一种便于软件实现的描述方式。

输入:

1. 明文 P &＃61; P1||P2||...||Pn&＃xff0c;n个64-bit
2. 密钥 K (KEK).

输出:

1. 密文 C &＃61; C0||C1||...||Cn,(n&＃43;1)个64-bit

步骤

1)  A &＃61; IV, IV &＃61; 0xA6A6A6A6A6A6A6A6

    For i &＃61; 1 to n, R[i] &＃61; P[i]

2)  For j &＃61; 0 to 5 {

        For i&＃61;1 to n {

            B &＃61; AES(K, A || R[i])

            A &＃61; MSB(64, B) ⊕ t,其中t &＃61; (n*j)&＃43;i

            R[i] &＃61; LSB(64, B)

        }//i

    }//j

3)  C[0] &＃61; A

For i &＃61; 1 to n, C[i] &＃61; R[i]

Return C &＃61; C[0] || C[1] || ... || C[n]

1. KWP

带填充的KW加密KWP-AE(P)和带填充的KW解密KWP-AD(C)。

加密C &＃61; KWP-AE(P)

输入&＃xff1a;明文P

输出&＃xff1a;密文C

1. ICV2 &＃61; 0xA65959A6.

2. 

3. PAD &＃61; 08×padlen

4. S &＃61; ICV2 || [len(P)/8]32 || P || PAD

5.  If len(P) ≤ 64,   return C &＃61; CIPHK(S);

else,            return C &＃61; W(S). 

这里的padlen是指将明文P填充为64bit的整数倍时需要填充&＃xff08;填充数据为全零字节&＃xff09;的最短字节数&＃xff0c;可以为0。消息S表示在填充后消息的前面再加64比特的特殊消息&＃xff0c;以保证S长度最少为一个分组大小&＃xff08;128bit&＃xff09;。如果S长度只有一个分组大小&＃xff0c;则直接执行AES。

解密P &＃61; KW-AD(C)

输入&＃xff1a;密文C&＃xff0c;C &＃61; C1||C2||...||Cn, n个64-bit

输出&＃xff1a;明文P或者失败

1.  ICV2 &＃61; 0xA65959A6.

2. If n &＃61; 2, S &＃61; CIPH-1K(C); if n > 2, S &＃61; W-1(C).

3. If MSB32(S) ≠ ICV2, return FAIL and stop.

4.  Plen &＃61; int(LSB32(MSB64(S))).

5. padlen &＃61; 8(n-1)-Plen.

6. If padlen <0 or padlen > 7, return FAIL and stop.

7. If LSB8×padlen(S) ≠ 08×padlen, return FAIL and stop.

8. Return P &＃61; MSB8×Plen(LSB64×(n-1)(S)).

1. TKW

这个和KW其实是一样的&＃xff0c;只有一下几个地方有区别&＃xff1a;

1. 使用的密码算法不一样&＃xff1a;KW采用AES&＃xff1b;TKW采用TDES
2. 分组大小不一样导致半分组大小不一样&＃xff1a;KW半分组大小64bit&＃xff1b;TKW半分组大小32bit。

详细流程可辅助参见KW。

注意&＃xff1a;TKW没有加填充的所谓TKWP算法。

1. 测试数据

NIST SP 800-38F里面没有测试数据&＃xff1b;测试数据可以在RFC 3394和RFC 5649里面查。

LibTomCrypt目前尚不支持KeyWrap。