马里奥AI实现方式探索：神经网络+增强学习

导语

在深圳的研发部培训中&＃xff0c;我们组给定一个有趣的课题便是&＃xff1a;马里奥游戏的智能通关&＃xff0c;本文就神经网络和增强学习两个点进行整理&＃xff0c;并将我们最后用的NEAT算法以及扩展找到的DRL算法进行了简单梳理。如果能够在游戏自动化测试、智能AI中应用这些有趣的算法&＃xff0c;想想还是有点小激动哒 ^v^

马里奥AI实现方式探索&＃xff1a;神经网络&＃43;增强学习

儿时我们都曾有过一个经典游戏的体验&＃xff0c;就是马里奥&＃xff08;顶蘑菇^v^&＃xff09;&＃xff0c;这次里约奥运会闭幕式&＃xff0c;日本作为2020年东京奥运会的东道主&＃xff0c;安倍最后也已经典的马里奥形象出现。平时我们都是人来玩马里奥游戏&＃xff0c;能否可以让马里奥智能的自己闯关个呢&＃xff1f;OK&＃xff0c;利用人工智能的相关算法来进行自动化通关一直是一个热门的话题&＃xff0c;最近最火的相关东东就是传说中的alphaGo啦。而在游戏的自动化测试当中&＃xff0c;这种算法也是非常实用的&＃xff0c;可以大量的减少测试人力成本。
首先&＃xff0c;对于实现马里奥AI当中涉及到的神经网络和增强学习的相关概念进行整理&＃xff0c;之后对智能通关的两种方式进行阐述。&＃xff08;本人才疏学浅&＃xff0c;在神经网络和增强学习方面基本门外汉&＃xff0c;如有任何纰漏&＃xff0c;还请大神指出&＃xff0c;我会第一时间改正。&＃xff09;

神经网络

像飞机的灵感来源于鸟类&＃xff0c;雷达的灵感来源于蝙蝠&＃xff0c;红外线的灵感来源于蛇&＃xff0c;而本文要讨论的神经网络灵感来源于我们自己&＃xff0c;人类大脑的神经元结构。从神经元结构被提出&＃xff0c;到时下火热的无以复加的深度神经网络&＃xff0c;发展过程也可为一波三折。我们按照时间的顺序&＃xff0c;对一些经典的神经网络模型进行整理&＃xff1a;

M-P模型

40年代初心理学家 W.W.Mcculloch 和梳理逻辑家 W.Pitts 提出 M-P 模型&＃xff08;为啥叫M-P模型&＃xff0c;看看这两位大牛的名字&＃xff0c;也不考虑下我们非英语系国家人民的感受。。。&＃xff09;&＃xff0c;神经网络被引入到计算机领域当中&＃xff0c;其最初起源的灵感就是人类大脑中的神经元&＃xff0c;如下图&＃xff1a;

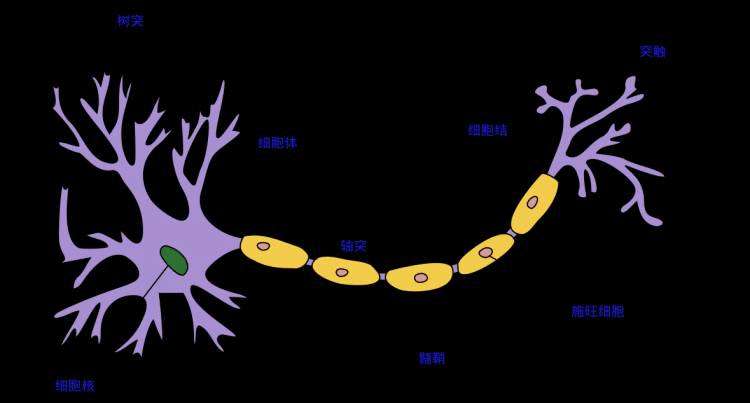
生物学上具体的专业术语我们这里不展开描述&＃xff0c;我们总结一下神经元结构的特点&＃xff1a;

• 每个神经元都是一个多输入单输出的信息处理单元&＃xff1b;
• 神经元输入分兴奋性输入和抑制性输入两种类型&＃xff1b;
• 神经元具有空间整合特性和阈值特性&＃xff1b;
• 神经元输入与输出间有固定的时滞&＃xff0c;主要取决于突触延搁。

由此两位大牛提出了神经网络的早期M-P模型&＃xff0c;如下图&＃xff1a;

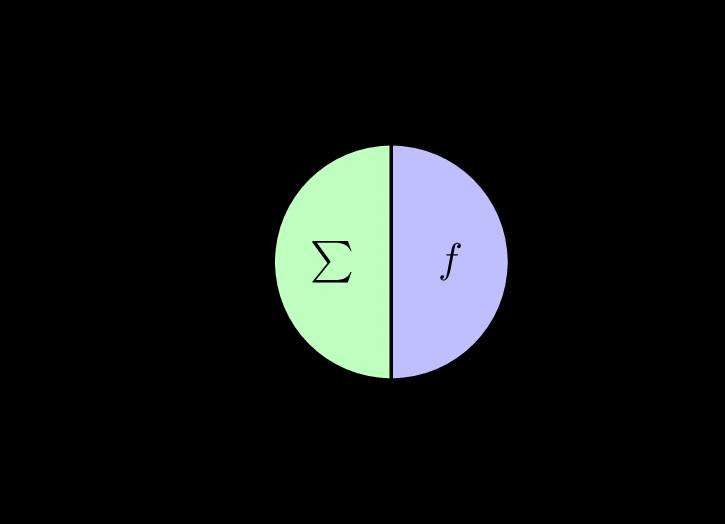
该模型的基本思想很简单&＃xff0c;就是仿照神经元接受多个输入信号&＃xff0c;由于突触的性质和突触强度不同&＃xff0c;所以对神经元的影响程度不同&＃xff0c;我们加上了权重的概念&＃xff0c;其正负模拟了神经元中的兴奋和抑制作用&＃xff0c;最后所有信号累加整合&＃xff0c;其值为&＃xff1a;

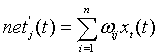
输入信号有了&＃xff0c;神经元是否被激活&＃xff0c;要看输入信号是否超过了某一阈值电位&＃xff0c;如果被激活神经元输出脉冲&＃xff0c;否则神经元不会输出信号&＃xff0c;其过程如下函数&＃xff1a;

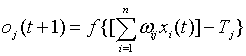
当然这里我们也可以写成矩阵的形式

类似神经元结构的特点&＃xff0c;经典的M-P模型的特点可以总结如下&＃xff1a;

1. 每个神经元都是一个多输入单输出的信息处理单元&＃xff1b;
2. 神经元输入分兴奋性输入和抑制性输入两种类型&＃xff1b;
3. 神经元具有空间整合特性和阈值特性&＃xff1b;
4. 神经元输入与输出间有固定的时滞&＃xff0c;主要取决于突触延搁&＃xff1b;
5. 忽略时间整合作用和不应期&＃xff1b;
6. 神经元本身是非时变的&＃xff0c;即其突触时延和突触强度均为常数。&＃xff08;神经网络中权重在训练结束后是固定的&＃xff09;

结合两个公式来看这几个特点&＃xff1a;对于特点1&＃xff0c;我们的公式有多个x输入信号&＃xff0c;但我们的输出信号只有一个o&＃xff1b;权重的正负体现了特点2中输入分兴奋和抑制&＃xff1b;对于第3个特点&＃xff0c;我们第2个公式中只有当输入信号的累加和超出电位阈值才会有输出&＃xff1b;另外我们的公式只考虑了所有输入信号的整合&＃xff0c;并没有去考虑时间整合&＃xff08;就是不管你信号早到晚到&＃xff0c;只要到了都是好信号&＃xff09;&＃xff0c;体现了特性4和5。

随着M-P模型的提出&＃xff0c;神经网络的研究有三次兴起&＃xff0c;最近的一次就是随着卷积神经网络提出的深度学习的火热。

早期神经网络

M-P模型很简单&＃xff0c;仅仅是一种单个神经元上的建模&＃xff0c;并没有形成网络&＃xff0c;没法去完成一些特定的任务。由此人们提出了神经网络的概念&＃xff0c;而早期的研究&＃xff0c;由于当时硬件水平和计算条件的限制&＃xff0c;神经网络结构一般比较简单。

两层神经网络

由此1958年&＃xff0c;计算科学家Rosenblatt提出了由两层神经元组成的神经网络。他给它起了一个名字“感知器”&＃xff08;Perceptron&＃xff09;
其结构如下图&＃xff1a;

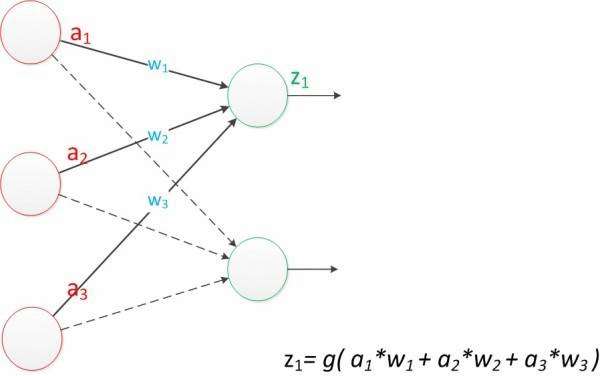
这种简单的单层神经网络有点类似于逻辑回归&＃xff0c;通过简单的权重训练&＃xff0c;能够处理简单的线性分类问题&＃xff0c;类似下图&＃xff1a;

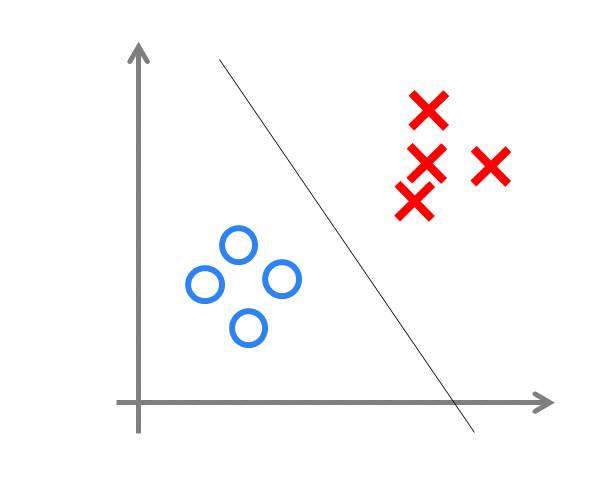
而对于非线性的分类问题&＃xff08;如经典的异或问题&＃xff09;却无能为力&＃xff0c;后来研究人员也发现了这一点&＃xff0c;神经网络研究遍进入了低谷期&＃xff08;好伤心TT&＃xff09;

三层神经网络&＃xff08;带有隐层&＃xff09;

问题总是用来解决的嘛&＃xff0c;既然两层神经网络hold不住非线性分类问题&＃xff0c;那么我们就加一层&＃xff0c;称为隐含层&＃xff0c;由此而来的三层神经网络如下图&＃xff1a;

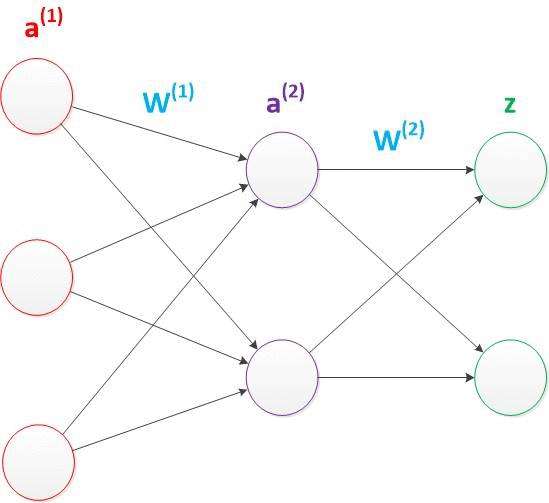
这种三层神经网络具有非常好的非线性分类效果&＃xff0c;其计算公式如下&＃xff1a;

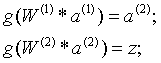
当然啦&＃xff0c;就像我们平时的逻辑回归模型一样&＃xff0c;bias在模型中是必不可少的&＃xff0c;所以我们在原有结构上加入偏置节点&＃xff0c;结构图如下&＃xff1a;

神经网络中偏置节点是默认存在的&＃xff0c;而且它非常特殊&＃xff0c;就是没有输入&＃xff0c;并且会输出的后一层的所有节点。加入偏置节点后计算公式如下&＃xff1a;&＃xff08;一般情况下&＃xff0c;偏置节点不会被画出来&＃xff09;

与两层神经网络不同&＃xff0c;理论证明三层神经网络能够无限逼近任意连续函数。这里我们不禁会有疑问&＃xff0c;我们知道两层神经网络是线性分类问题&＃xff0c;那么两个线性问题拼在一起为什么就可以解决非线性分类问题了呢&＃xff1f;

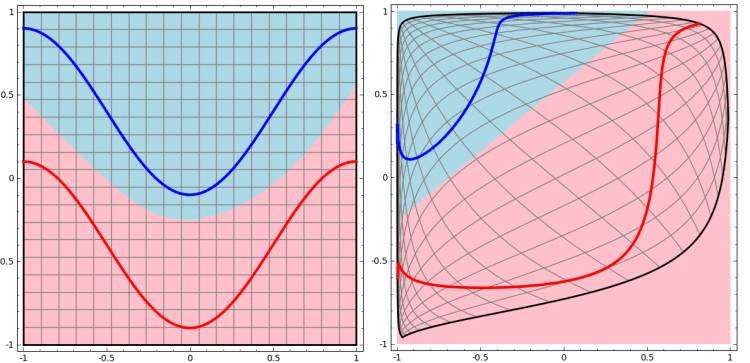
上图很好的解释了我们的疑问。首先上图左侧部分可以看出&＃xff0c;三层神经网络的决策分界非常平滑&＃xff0c;而且分类的很好。而上图右侧部分展示了该图经过空间变换后的结果&＃xff0c;我们可以看到输出层的决策分界仍然是直线&＃xff0c;关键是&＃xff0c;从输入层到隐含层时&＃xff0c;发生了空间变换。
也就是说三层神经网络可以做非线性分类的关键便是隐含层的加入&＃xff0c;通过矩阵和向量相乘&＃xff0c;本质做了一次线性变换&＃xff0c;使得原先线性不可分的问题变得线性可分。所以多层神经网络本质就是复杂函数的拟合。
现在三层神经网络结构定了&＃xff0c;如何来进行网络的训练&＃xff0c;这就需要用到反向传播算法&＃xff08;本质就是梯度下降&＃xff0c;还说的这儿玄乎<-T->&＃xff09;

BP算法

上面我们提到两层神经网络&＃xff0c;其中隐层的权值是需要我们学习的&＃xff0c;而这个权值我们不能直接获取&＃xff0c;所以我们利用输出层得到输出结果和期望输出的误差来间接调整隐层的权值。BP算法的学习过程由信号的正向传播和误差的反向传播两个过程组成。

• 正向传播时,输入样本从输入层传入,经各隐层逐层处理后,传向输出层。若输出层的实际输出与期望的输出(教师信号)不符,则转入误差的反向传播阶段。
• 反向传播时&＃xff0c;将输出以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。

下图展示了整个BP算法的信号流程图&＃xff1a;

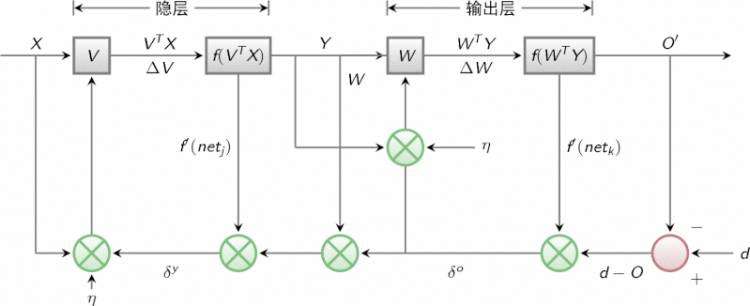
BP网络有三个要素&＃xff1a;

1. 网络拓扑结构
2. 传递函数
3. 学习算法

网络拓扑结构便是我们之前总结的两层神经网络结构&＃xff0c;我们主要从传递函数和学习算法进行整理阐述下。

传递函数

首先什么是传递函数呢&＃xff1f;请看下图&＃xff1a;

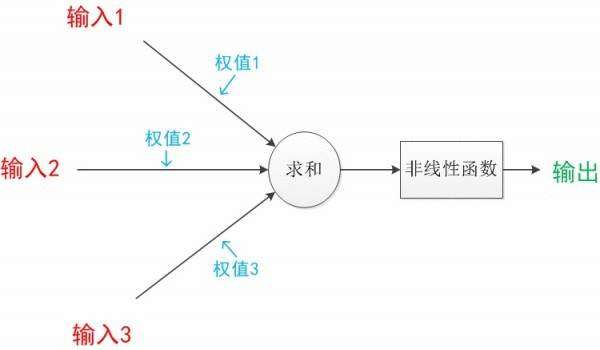
图中是最基本的单个神经元的模型&＃xff0c;针对于多个输入&＃xff0c;我们会进行整合并利用一个非线性函数进行输出&＃xff0c;函数的要求必须是可微单调递增函数&＃xff0c;通常采用非线性变换函数———sigmoid函数也称S函数&＃xff08;形状&＃xff09;&＃xff0c;有单极性S型函数和双极性S型函数两种&＃xff08;高中数学里的东东&＃xff09;。

• 单极性S型函数定义如下&＃xff1a;

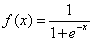
函数曲线图如下&＃xff08;似乎不够S。。&＃xff09;

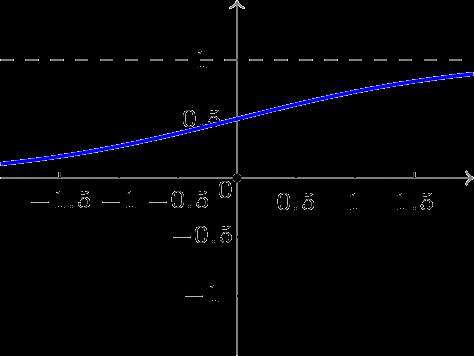
双极性S型函数定义如下&＃xff1a;

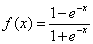
函数曲线图如下&＃xff1a;

可以看出根据上面的S函数&＃xff0c;我们会整合所有输入&＃xff0c;输出一个新的值&＃xff0c;从之前生物学的原理来看也就是说神经元是否被激活。

学习算法

学习算法是BP神经网络结构的核心&＃xff0c;也是两层神经网络有一次兴起的重要原因&＃xff0c;因为人们找到了如何去训练一个神经网络来达到我们预期的分类效果&＃xff08;拟合不同的非线性连续函数&＃xff09;。而BP算法&＃xff08;反向传播算法&＃xff09;的本质其实就是一种逐层梯度下降。

我们以三层感知器为例&＃xff0c;当网络输出与期望输出不一致时&＃xff0c;存在误差E&＃xff0c;定义如下&＃xff1a;

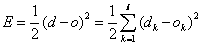
将以上误差反向逐层展开&＃xff08;体现了反向传播算法中的反向含义&＃xff09;

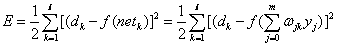
最终我们展开到输入层如下&＃xff1a;

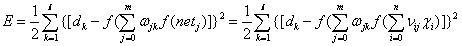
根据上式我们发现误差E是的函数&＃xff0c;我们发现调整权值可以改变误差E的大小&＃xff0c;而调整权值的原则是使得误差不断减小。因此我们应该使得权值与误差的梯度下降成正比&＃xff0c;如下&＃xff1a;

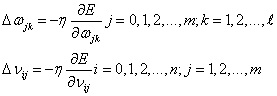
其中值得注意的是表示学习效率&＃xff0c;即权重调整的幅度。
我们可以看出对于权重的调整是从输出层逐层反传过来的&＃xff0c;而且我们也发现我们在梯度下降的过程中需要求导&＃xff0c;这也就是我们在最初要求传递函数可微的原因

深度神经网络

有三层神经网络&＃xff0c;我们自然而然就会想到将神经网络加入更多层&＃xff0c;扩展到深度神经网络&＃xff0c;但是一个非常显著的问题就是参数的个数&＃xff0c;比如之前我们的三层神经网络每层有1000个节点&＃xff0c;那么我们需要调整的权值参数就达到了10^9量级&＃xff0c;这问题限制了很大程度上限制了深度神经网络的发展。这就要把大哥叫出来帮忙了&＃xff0c;就是近期一直火热的deep learning&＃xff0c;由于本人在这方面也是门外汉&＃xff0c;只从经典的卷积神经网络&＃xff08;CNN&＃xff09;进行一些归纳整理。

CNN的解决之道

根据网上的资料总结&＃xff0c;CNN的核心点有三个&＃xff1a;

• 局部感知&＃xff1a;形象地说&＃xff0c;就是模仿你的眼睛&＃xff0c;想想看&＃xff0c;你在看东西的时候&＃xff0c;目光是聚焦在一个相对很小的局部的吧&＃xff1f;严格一些说&＃xff0c;普通的多层神经网络&＃xff0c;隐层节点会全连接到一个图像的每个像素点上&＃xff0c;而在卷积神经网络中&＃xff0c;每个隐层节点只连接到图像某个足够小局部的像素点上&＃xff0c;从而大大减少需要训练的权值参数。我们用两张对比图来说明下&＃xff1a;

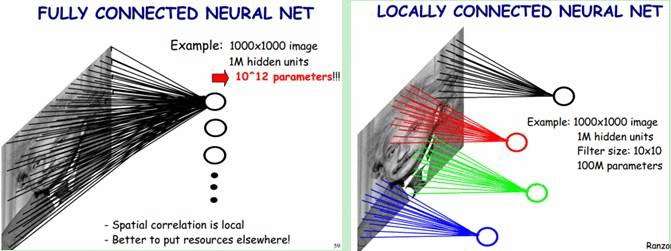
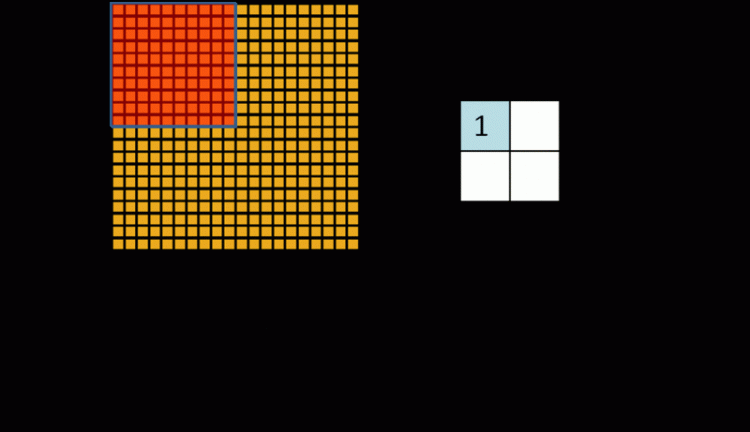
从图中我们可以看出&＃xff0c;对于一张1000×1000像素的图片&＃xff0c;假设神经网络中的隐节点有1M个。对于传统的深度神经网络&＃xff0c;所有的隐节点会连接到图像中的每个像素点&＃xff0c;那么我们需要训练的权重参数就达到了匪夷所思的10^12量级。而CNN提出局部感知&＃xff0c;即图中右侧展示的&＃xff0c;每个神经元只与10×10个像素值相连&＃xff0c;那么我们的权重参数就下降到10^8&＃xff0c;参数数量为原来的万分之一&＃xff08;虽然还是很多TT&＃xff09;

• 权值共享&＃xff1a;形象地说&＃xff0c;就如同你的某个神经中枢中的神经细胞&＃xff0c;它们的结构、功能是相同的&＃xff0c;甚至是可以互相替代的。局部感知的方式在一定程度上减少了参数&＃xff0c;那么另一个减少参数的神器便是权值共享。在上面我们提到的局部感知的例子中&＃xff0c;对于1M个神经元&＃xff0c;每个神经元需要局部感知10×10个像素点&＃xff0c;那么参数个数是100×1M个&＃xff0c;那么如果我们在这里假设每个神经元的权重参数都是相同的&＃xff0c;那么我们的参数个数就会骤减到100个&＃xff0c;很夸张对不拉&＃xff0c;做到这一步的神器便是卷积操作。

权值共享基于的原理或者说假设是图像中局部的统计特征与其他部分是一样的&＃xff0c;也就意味着假设我们在图像的局部学习到了一组特征&＃xff0c;那么我们可以直接将这组特征应用到图像的其它部分。就拿上面的例子来看&＃xff0c;我们假设在第一个神经元中学习到了局部10×10像素点的特征&＃xff0c;那么我们完全可以将这个特征应用在图像的其他位置上&＃xff0c;那么我们另外的1M-1的神经元权重参数就不需要训练了&＃xff0c;所以我们只需要训练第一个神经元的权重参数即可&＃xff0c;而这第一个神经元得到的局部特征称为卷积核。当然啦&＃xff0c;我们不会这么变态的只用一个卷积核&＃xff0c;这样对于图像特征的提取也是不充分的&＃xff0c;所以往往CNN中都会有多个卷积核来进行卷积操作&＃xff0c;每个卷积核会提取出图像某一方面的特征。如下图展示了卷积操作的基本原理&＃xff1a;

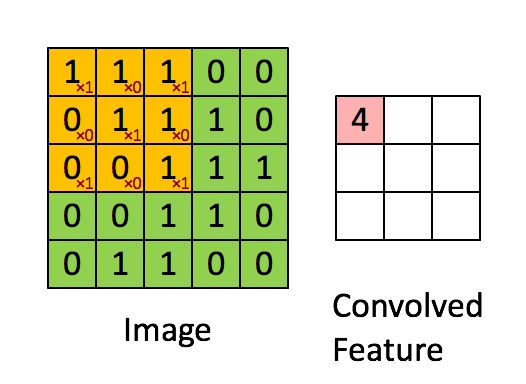
图中展示了一个3×3的卷积核在5×5的图像上做卷积的过程。每个卷积都是一种特征提取方式&＃xff0c;就像一个筛子&＃xff0c;将图像中符合条件&＃xff08;激活值越大越符合条件&＃xff09;的部分筛选出来。

• 池化&＃xff1a;形象地说&＃xff0c;你先随便看向远方&＃xff0c;然后闭上眼睛&＃xff0c;你仍然记得看到了些什么&＃xff0c;但是你能完全回忆起你刚刚看到的每一个细节吗&＃xff1f;不能&＃xff08;也没必要&＃xff09;&＃xff0c;我们通常会提取整个图像中一些关键的点作为一种“映像”放到脑海中。同样&＃xff0c;在卷积神经网络中&＃xff0c;通过卷积获得了特征之后&＃xff0c;下一步我们需要利用这些特征去做分类&＃xff0c;当然我们可以利用所有这些特征去做分类&＃xff08;如softmax分类器&＃xff09;&＃xff0c;但同样的这里又会遇到我们的老问题&＃xff0c;计算量过大。所以&＃xff0c;在进行分类之前&＃xff0c;我们利用人类判别图片记录关键特征的原理&＃xff0c;同样在处理卷积层输出的特征时&＃xff0c;我们也可以做一些“压缩”或者说提取处理&＃xff0c;这种方法被称为池化&＃xff08;Down-pooling&＃xff09;。以最大池化&＃xff08;Max Pooling&＃xff09;为例&＃xff0c;1000×1000的图像经过10×10的卷积核卷积后&＃xff0c;得到的是991×991的特征图&＃xff08;参考上图5×5图像经过卷及操作变成了3×3的图像&＃xff09;&＃xff0c;然后使用2×2的池化规模&＃xff0c;即每4个点组成的小方块中&＃xff0c;取最大的一个作为输出&＃xff0c;最终得到的是496×496大小的特征图。池化得原理我们可以用下图形象的说明&＃xff1a;

CNN整体结构

上面我们从CNN的三个核心点出发&＃xff0c;阐述了CNN的基本原理&＃xff0c;下图我们列出了CNN的整体结构&＃xff1a;

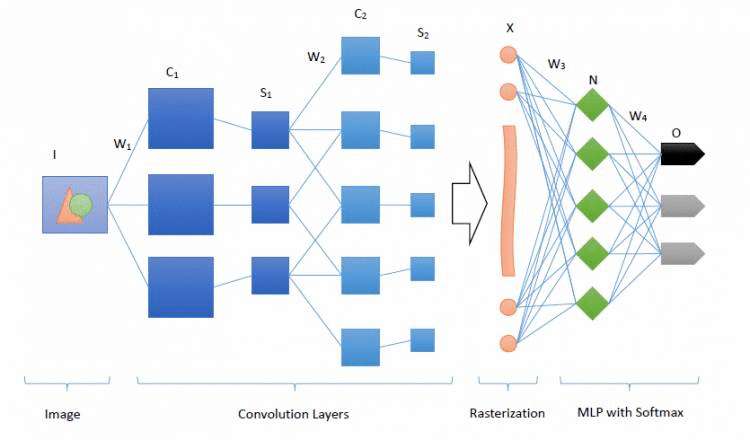
图中从左至右描述了CNN神经网络的几个不同层

• 输入层&＃xff08;图像&＃xff09;&＃xff1a;在CNN神经网络的输入当中&＃xff0c;一般为了减少复杂度&＃xff0c;往往采用灰度化后的图像作为输入&＃xff0c;而如果使用RGB的彩色图像&＃xff0c;那么输入会分为RGB三个分量图像。输入图像一般都需要归一化&＃xff0c;常规的可以使用我们前面阐述的sigmoid函数&＃xff0c;归一化到[0,1]&＃xff0c;如果使用tanh激活函数&＃xff0c;则归一化到[-1, 1]。这一部分我们涉及到了我们上面阐述的局部感知的方式来减少参数。

• 多个卷积&＃xff08;C&＃xff09;-下采样&＃xff08;S&＃xff09;层&＃xff1a;将上一层的输出与本层权重W做卷积得到各个C层&＃xff0c;然后下采样得到各个S层&＃xff0c;这一部分主要涉及了我们上面阐述的三个核心点中的卷积和池化操作&＃xff0c;而这些层的输出称为Feature Map。

• 光栅化&＃xff08;X&＃xff09;&＃xff1a;是为了与传统的多层感知器全连接。即将上一层的所有Feature Map的每个像素依次展开&＃xff0c;排成一列。

• 传统的多层感知器&＃xff08;N&O&＃xff09;:最后的分类器一般使用Softmax&＃xff0c;如果是二分类&＃xff0c;当然也可以使用逻辑回归LR。
  至此关于CNN的基本原理基本阐述完毕啦&＃xff0c;关于CNN的参数训练等内容这里不再赘述&＃xff0c;可以参考Deep learning&＃xff1a;五十一(CNN的反向求导及练习)

总结

~长出一口气~&＃xff0c;从最一开始单个神经元模型的提出&＃xff0c;到两层和三层的简单神经网络&＃xff0c;再到时下火热的深度学习&＃xff0c;我们可以用下图从时间上进行一个大致的梳理&＃xff1a;

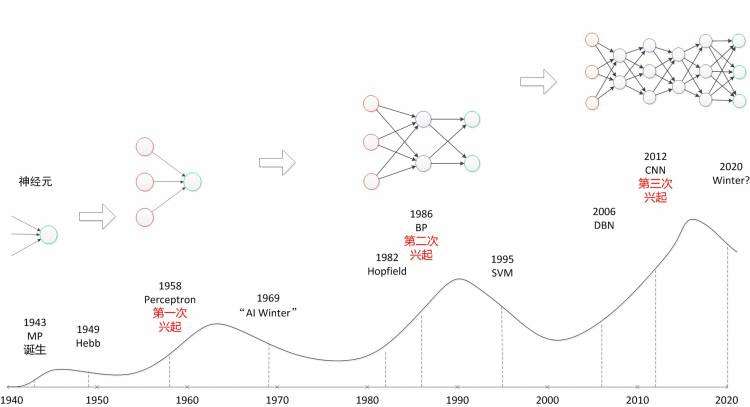
我们可以看到&＃xff0c;神经网络的发展经历了三次跌宕起伏&＃xff1a;

• 感知器&＃xff1a;第一次兴起的研究点便是科研人员利用两层神经网络&＃xff08;起了个玄乎的名字感知器&＃xff09;进行了简单的分类问题&＃xff0c;当时的人们大呼找到了人工智能的奥秘&＃xff0c;从而兴起了对神经网络的研究&＃xff0c;但是随着众多学者发现两层感知器只能完成最简单的线性分类问题&＃xff0c;对于经典的异或分类问题都无法完成时&＃xff0c;神经网络陷入低谷。

• BP算法&＃xff1a;第二次兴起的关键点便是BP算法的提出&＃xff0c;当人们发现两层神经网络无法胜任非线性分类问题时&＃xff0c;已经想到了增加神经网络层数&＃xff0c;但是随着网络层数的增加&＃xff0c;权重参数如何训练的问题无法解决&＃xff0c;直到BP反向传播算法的提出&＃xff0c;解决了这一问题&＃xff0c;从而发生了神经网络的又一次兴起。但是随之而来的其它算法&＃xff0c;如SVM&＃xff0c;等算法的提出&＃xff0c;人们发现这些算法的通用性和可计算性都优于神经网络&＃xff0c;神经网络进入到了第二次低谷。

• 深度学习&＃xff1a;第三次兴起的关键点便是时下火热的深度学习了&＃xff0c;它的标致之一便是CNN卷积神经网络的提出&＃xff0c;将它用于图像分类问题当中&＃xff08;当然了这也离不开硬件水平的提高&＃xff0c;比如高并行的GPU诞生&＃xff09;。

而对于每次神经网络可解决的问题&＃xff0c;我们可以用下图来阐述&＃xff1a;

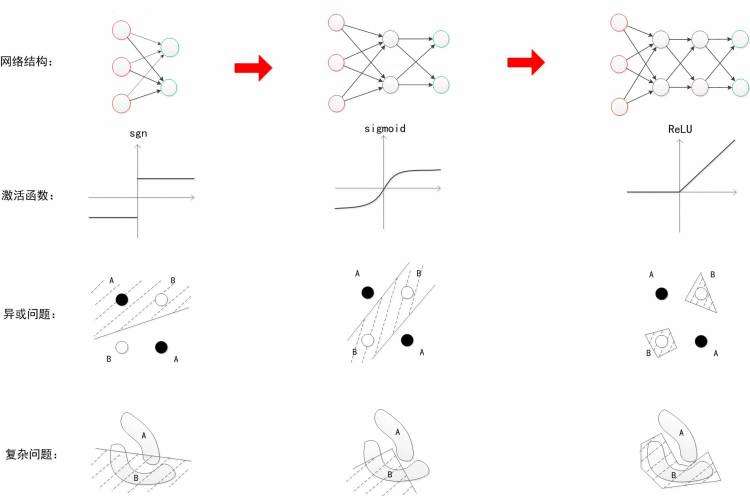
上图中我们可以看出&＃xff0c;随着神经网络的发展&＃xff0c;我们在解决最基本的分类问题时的效果越来越好&＃xff0c;这也是神经网络的魅力所在啦^v^。当然在神经网络发展的过程当中&＃xff0c;计算机硬件水平的发展也是不容忽视的&＃xff0c;随着计算能力和性能的提高&＃xff0c;原来不可能实现的想法、算法都能付诸实践进行试验。

增强学习

机器学习领域&＃xff0c;我们都知道两位大哥就是监督学习和非监督学习&＃xff0c;我们有样本X和标记或者未标记的Y&＃xff0c;我们通过训练可以做一些分类或者聚类的任务。但是&＃xff0c;对于一些序列决策或者控制问题&＃xff0c;是很难得到上面那样的规则样本的&＃xff0c;比如机器人的控制问题&＃xff0c;决策机器人下一步该怎么走&＃xff0c;那么这时我们就需要清楚另外一位大哥——增强学习&＃xff0c;虽然他似乎曝光度并不是很高&＃xff0c;那么何谓增强学习呢&＃xff1f;

增强学习&＃xff08;Reinforcement Learning, RL&＃xff09;&＃xff0c;其英文定义如下&＃xff1a;

Reinforcement learning is learning what to do ——how to map situations to actions —— so as to maximize a numerical reward signal.[6]

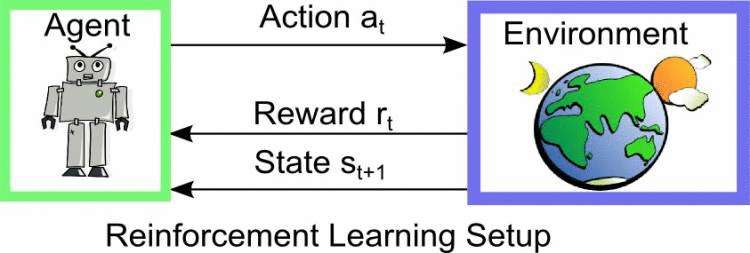
也就是说增强学习关注的是智能体如何在环境中采取一系列行为&＃xff0c;从而获得最大的累积回报。

通过增强学习&＃xff0c;一个智能体&＃xff08;agent&＃xff09;应该知道在什么状态下应该采取什么行为。RL是从环境状态到动作的映射的学习&＃xff0c;我们把这个映射称为策略。

马尔可夫决策过程&＃xff08;MDP&＃xff09;

一提到马尔科夫&＃xff0c;大家通常会立刻想起马尔可夫链&＃xff08;Markov Chain&＃xff09;以及机器学习中更加常用的隐式马尔可夫模型&＃xff08;Hidden Markov Model, HMM&＃xff09;。它们都具有共同的特性便是马尔可夫性&＃xff1a;当一个随机过程在给定现在状态及所有过去状态情况下&＃xff0c;其未来状态的条件概率分布仅依赖于当前状态&＃xff1b;换句话说&＃xff0c;在给定现在状态时&＃xff0c;它与过去状态&＃xff08;即该过程的历史路径&＃xff09;是条件独立的&＃xff0c;那么此随机过程即具有马尔可夫性质。具有马尔可夫性质的过程通常称之为马尔可夫过程。[7]

之后我们便来说说马尔可夫决策过程&＃xff08;Markov Decision Process&＃xff09;&＃xff0c;其也具有马尔可夫性&＃xff0c;与上面不同的是MDP考虑了动作&＃xff0c;即系统下个状态不仅和当前的状态有关&＃xff0c;也和当前采取的动作有关。

用表格描述马尔可夫各个模型的关系&＃xff08;摘自[8]&＃xff09;

基本定义

一个马尔可夫决策过程由五元组组成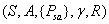

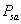• S&＃xff1a;表示状态集&＃xff08;states&＃xff09;
• A&＃xff1a;表示一系列动作&＃xff08;actions&＃xff09;
• &＃xff1a;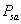表示状态转移概率。表示的是在当前s ∈ S状态下&＃xff0c;经过a ∈ A作用后&＃xff0c;会转移到的其他状态的概率分布情况。比如&＃xff0c;在状态s下执行动作a&＃xff0c;转移到s’的概率可以表示为p(s’|s,a)。

&＃xff08;dicount factor&＃xff09;&＃xff1a;表示阻尼系数[0,1)

• R&＃xff1a;&＃xff0c;表示回报函数&＃xff08;reward function&＃xff09;
  MDP 的动态过程如下&＃xff1a;某个智能体(agent)的初始状态为s0&＃xff0c;然后从 A 中挑选一个动作a0执行&＃xff0c;执行后&＃xff0c;agent 按概率随机转移到了下一个s1状态&＃xff0c;s1∈ 
  。然后再执行一个动作a1&＃xff0c;就转移到了s2&＃xff0c;接下来再执行a2…&＃xff0c;我们可以用下面的图表示状态转移的过程。

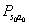
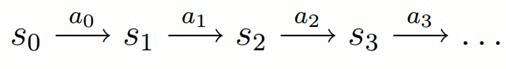
如果回报r是根据状态s和动作a得到的&＃xff0c;则MDP还可以表示成下图&＃xff1a;

值函数

上面我们给出了MDP的定义&＃xff0c;作为一个智能体&＃xff08;agent&＃xff09;&＃xff0c;当它在决定下一步应该走什么时&＃xff0c;最简单的方式就是看下Reward函数的值是多少&＃xff0c;即比较走不同动作的回报&＃xff0c;从而做出决定。但是就像下棋的时候&＃xff0c;我们每走一步都会向后考虑&＃xff0c;所谓“走一步看三步”&＃xff0c;所以这里我们只看一步即一次Reward函数是不够的&＃xff0c;这就引出了值函数&＃xff08;Value Function&＃xff09;也叫折算累积回报&＃xff08;discounted cumulative reward&＃xff09;。

状态值函数&＃xff08;state value function&＃xff09;

当我们遵循某个策略&＃xff0c;我们将值函数定义如下&＃xff1a;

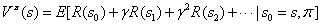
我们将上面的式子写作递推的样子如下&＃xff1a;

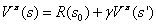
另外当策略&＃xff0c;在状态s时&＃xff0c;我们可以确定唯一的动作a&＃xff0c;但是s经过动作a会进入哪个状态是不唯一的&＃xff0c;比如同样是掷骰子操作&＃xff0c;可能得到的状态有6种&＃xff0c;那么利用Bellman等式我们便可以得到下面的公式&＃xff1a;

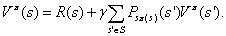
再根据我们最初增强学习的目的&＃xff0c;我们便可以得出&＃xff0c;求V的目的就是想找到一个当前状态s下&＃xff0c;最优的行动策略&＃xff0c;表示如下&＃xff1a;

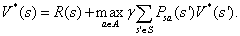
动作值函数&＃xff08;action value function&＃xff09;

上面我们的值函数的只与状态s有关&＃xff0c;如果与状态s和动作a都有关&＃xff0c;便称为动作值函数&＃xff0c;即所谓的Q函数&＃xff0c;如下&＃xff1a;

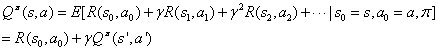
从上式我们可以看出&＃xff0c;我们不仅仅依赖状态s和策略&＃xff0c;并且还依赖于动作a。

综上我们可以将MDP的最优策略定义如下&＃xff1a;

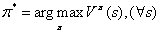
关于MDP的求解主要分为值迭代和策略迭代&＃xff0c;分别站在不同的角度对MDP进行求解&＃xff0c;这里我们不在赘述&＃xff0c;网上有很多相关资料。下面我们简单阐述下动作值函数的值迭代求解方式&＃xff0c;即所谓的Q-learning

Q学习

Q学习的基本迭代公式如下&＃xff1a;

从公式中我们也可以看出它是一种值迭代方式&＃xff0c;因为我们每次更新的是Q函数的值&＃xff0c;而非策略。简单起见&＃xff0c;整理一个简单的例子加以说明。

假设我们有这样一个房间&＃xff1a;

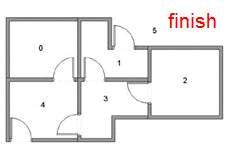
我们的目的是训练一个机器人&＃xff0c;使得它在图中的任意一个房间都能够到达房间外。

OK&＃xff0c;我们对房间进行建模&＃xff1a;

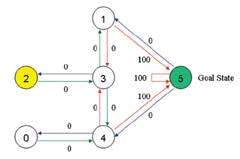
并得到reward矩阵&＃xff1a;

通过一下过程的迭代我们最终得出了我们的结果Q矩阵

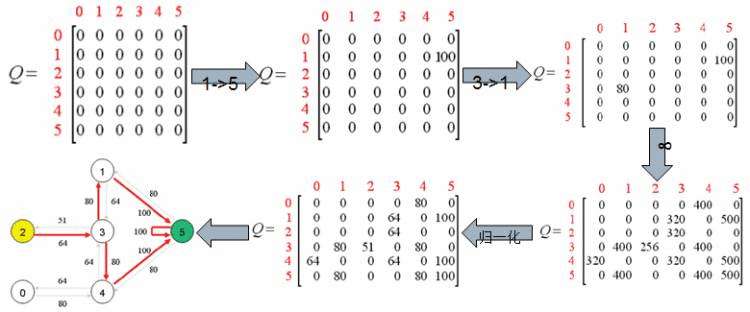
可以看出&＃xff0c;我们的机器人现在无论在哪个房间&＃xff0c;都可以利用我们的Q矩阵顺利的走到屋外。

噗噗噗&＃xff0c;终于写到这里了&＃xff0c;综上我们将马里奥只能AI需要用到的算法简单整理了下&＃xff08;如有任何谬误请指出^v^&＃xff09;。下面我们结合两种成熟的算法&＃xff0c;归纳整理马里奥AI的两种实现方式。

基于NEAT算法的马里奥AI实现

所谓NEAT算法即通过增强拓扑的进化神经网络&＃xff08;Evolving Neural Networks through Augmenting Topologies&＃xff09;&＃xff0c;算法不同于我们之前讨论的传统神经网络&＃xff0c;它不仅会训练和修改网络的权值&＃xff0c;同时会修改网络的拓扑结构&＃xff0c;包括新增节点和删除节点等操作。
NEAT算法几个核心的概念是&＃xff1a;

• 基因&＃xff1a;网络中的连接
• 基因组&＃xff1a;基因的集合
• 物种&＃xff1a;一批具有相似性基因组的集合
• Fitness&＃xff1a;有点类似于增强学习中的reward函数
• generation&＃xff1a;进行一组训练的基因组集合&＃xff0c;每一代训练结束后&＃xff0c;会根据fitness淘汰基因组&＃xff0c;并且通过无性繁殖和有性繁殖来新增新的基因组
• 基因变异&＃xff1a;发生在新生成基因组的过程中&＃xff0c;可能会出现改变网络的权重&＃xff0c;增加突出连接或者神经元&＃xff0c;也有可能禁用突触或者启用突触

下图我们展示了算法从最一开始简单的神经网络&＃xff0c;一直训练到后期的网络

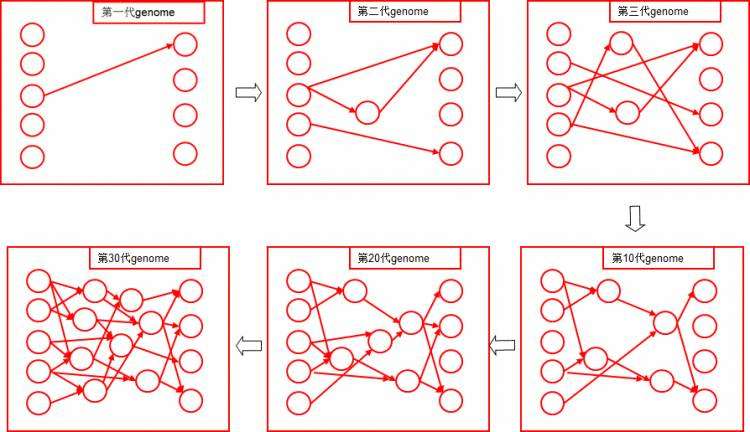
利用NEAT算法实现马里奥的只能通关的基本思想便是&＃xff0c;利用上面NEAT算法的基本观点&＃xff0c;从游戏内存中获取实时的游戏数据&＃xff0c;判断马里奥是否死忙、计算Fitness值、判断马里奥是否通关等&＃xff0c;从而将这些作为神经网络的输入&＃xff0c;最后输出对马里奥的操作&＃xff0c;包括上下左右跳跃等操作&＃xff0c;如下图&＃xff1a;

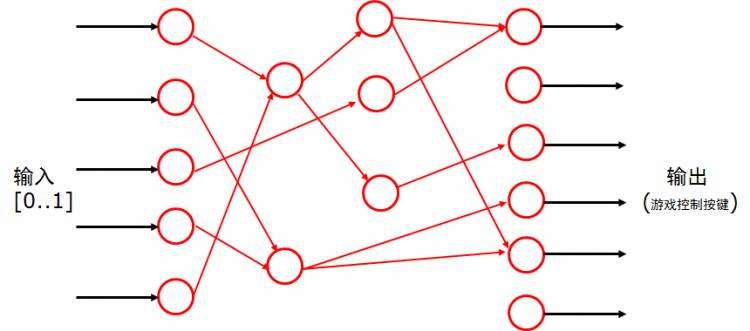
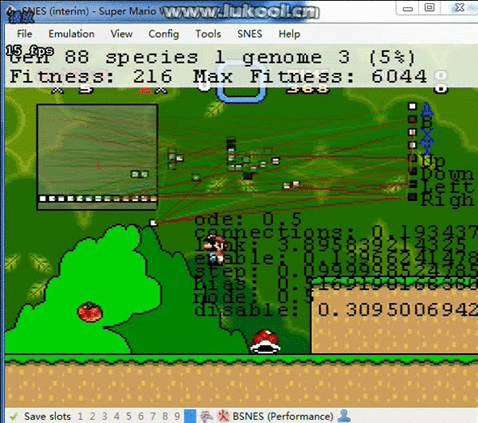
大多数该算法实现马里奥的智能通关都依赖于模拟器&＃xff0c;运用lua语言编写相应脚本&＃xff0c;获取游戏数据并操作马里奥。NeuroEvolution with MarI/O。实现效果图如下&＃xff1a;

基于Deep Reinforcement Learning的马里奥AI实现

NEAT算法是相对提出较早的算法&＃xff0c;在2013年大名鼎鼎的DeepMind提出了一种深度增强学习的算法&＃xff0c;该算法主要结合了我们上面讨论的CNN和Q-Learning两种算法&＃xff0c;DeepMind的研究人员将该算法应用在Atari游戏机中的多种小游戏中进行AI通关。

其基本算法核心便是我们之前介绍的CNN和增强学习的Q-Learning&＃xff0c;游戏智能通关的基本流程如下图&＃xff1a;

利用CNN来识别游戏总马里奥的状态&＃xff0c;并利用增强学习算法做出动作选择&＃xff0c;然后根据新的返回状态和历史状态来计算reward函数从而反馈给Q函数进行迭代&＃xff0c;不断的训练直到游戏能够通关。研究人员在训练了一个游戏后&＃xff0c;将相同的参数用在别的游戏中发现也是适用的&＃xff0c;说明该算法具有一定的普遍性。下图反映了一个学习的过程

而同样的方法&＃xff0c;将DRL应用在马里奥上&＃xff0c;github上有一个开源的实现方式&＃xff1a;aleju/mario-ai

其最终的实现效果图如下&＃xff1a;

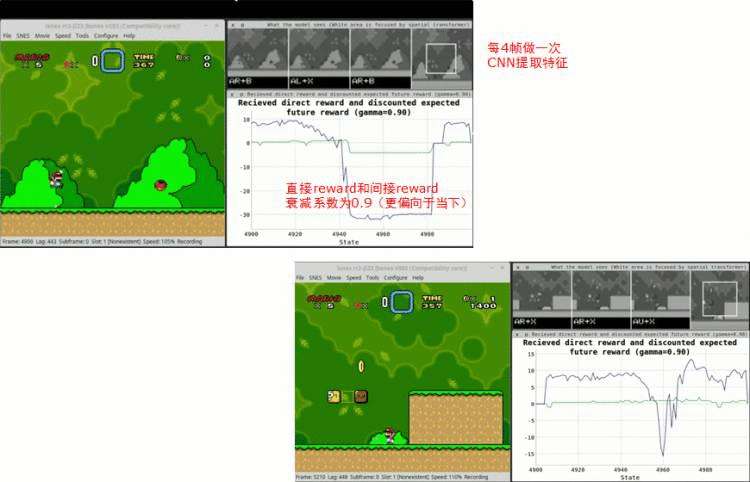
我们发现在CNN识别过程中&＃xff0c;每4帧图像&＃xff0c;才会进行一次CNN识别&＃xff0c;这是识别速率的问题&＃xff0c;图中曲线反映了直接回报函数和简介回报函数。

总结

综上便是从最基本的神经网络算法&＃43;增强学习&＃xff0c;到将这些算法用在智能AI上的一些基本整理&＃xff0c;长舒一口气&＃xff0c;整理了好久。。。关于智能AI的应用有很多&＃xff0c;也跟好多小伙伴讨论过&＃xff0c;包括智能测试、新式游戏、游戏平衡性调整以及AI机器人的加入。这个领域除了枯燥的理论知识还能玩游戏&＃xff0c;想想有点小激动。总结完毕&＃xff0c;如有任何纰漏还请指出&＃xff0c;我会尽快修改&＃xff0c;谢谢^v^。

最后感谢smurfyu(于洋)、apache(何庆玮)的指导以及小伙伴lufyzhang(张宇飞)、youngywang(王洋)、supercwang(王超)、bingyanshi(施冰燕)

参考文献&＃xff1a;

漫谈ANN(1)&＃xff1a;M-P模型
漫谈ANN(2)&＃xff1a;BP神经网络
卷积神经网络
卷积神经网络全面解析
重磅&＃xff01;神经网络浅讲&＃xff1a;从神经元到深度学习
R.Sutton et al. Reinforcement learning: An introduction , 1998
马尔可夫性质
增强学习&＃xff08;二&＃xff09;——- 马尔可夫决策过程MDP
增强学习&＃xff08;三&＃xff09;——- MDP的动态规划解法
增强学习&＃xff08;Reinforcement Learning and Control&＃xff09;
wiki-Q-learning
Q-Learning example
Stanley K O, Miikkulainen R. Evolving neural networks through augmenting topologies[J]. Evolutionary computation, 2002, 10(2): 99-127.
Wang Y, Schreiber B. Creating a Traffic Merging Behavior Using NeuroEvolution of Augmenting Topologies[J]. 2015.
Cussat-Blanc S, Harrington K, Pollack J. Gene regulatory network evolution through augmenting topologies[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(6): 823-837.
Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[J]. arXiv preprint arXiv:1312.5602, 2013.

转自&＃xff1a;
https://www.qcloud.com/community/article/375819