在聚类过程中需要生成人工数据集,代码及运行结果如下:
mul=[0,0]; % 均值
S1=[.1 0;0 .1]; % 协方差
data1=mvnrnd(mul, S1, 300); % 产生高斯分布数据
% 第二组数据
mu2=[1.25 1.25];
S2=[.1 0;0 .1];
data2=mvnrnd(mu2,S2,300);
% 第三组数据
mu3=[-1.25;1.25];
S3=[.1 0;0 .1];
data3=mvnrnd(mu3,S3,300);
% 显示数据
plot(data1(:,1),data1(:, 2),‘bo’);
hold on;
plot(data2(:,1),data2(:,2),‘r+’);
plot(data3(:,1),data3(:,2),‘g+’);
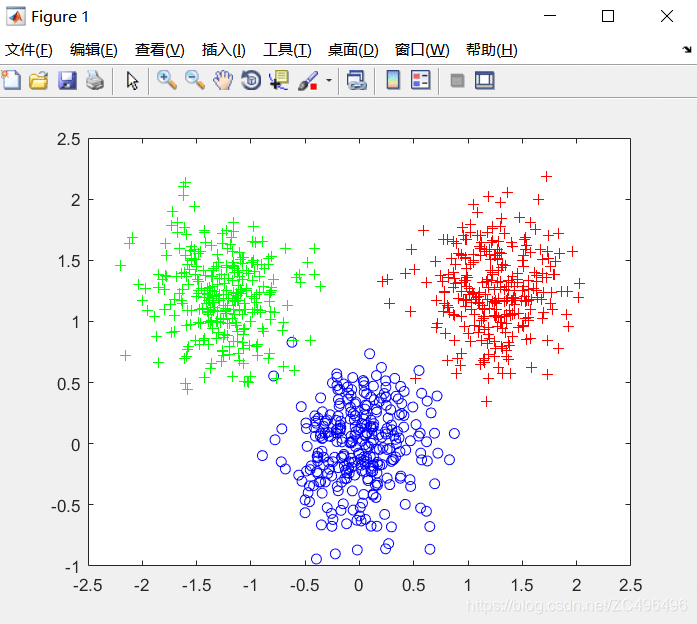
但是,如何生成理想中的形状?这就需要对此代码进行深入理解:
1、什么是协方差?
标准差和方差一般是用来描述一维数据的,协方差就是一种用来度量两个随机变量关系的统计量。
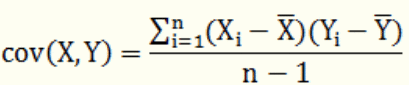
协方差的结果有什么意义呢?如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义);如果结果为负值, 就说明两者是负相关;如果为0,则两者之间没有关系,就是统计上说的“相互独立”。
2、什么是协方差矩阵?
SIGMA 是需要生成的数据的自相关矩阵(相关系数矩阵)

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有