论文笔记ORBSLAM2双目与rgbd相机跟单目情况的区别

ORB-SLAM2的最大贡献就是把原来的系统扩展到了双目，rgbd上，这一篇也主要讲的是怎么使用双目或者深度相机的信息，以及他们和单目的区别。

I.INTRODUCTION

1. Place Recognition是SLAM中一个对回环很重要的模块，作用是：1）检测传感器是否返回已经建过图的区域。2）修正累计误差。 3）在追踪失败之后重新定位相机。
2. 单目SLAM的优缺点：

• 优点：成本更低，传感器配置更简单
• 缺点：由于无法直接获得深度信息，所以就需要利用多视图或者滤波来生成初始地图（在最开始无法进行三角化）；会有尺度漂移；纯旋转时可能会失效。（如果用双目或者rgbd相机，所有的缺点都可以被解决）

3. 主要贡献中的两个亮点：

• RGB-D结果表明使用BA能比sota的ICP或者基于光度和深度误差最小化的方法更准。
• 通过使用近距离和远距离立体点和单目观测结果，我们的立体结果比sota的直接法立体 SLAM 更准确。

II.RELATED WORK

双目SLAM

• 文献[5]第一次使用了近点和远点（双目相机中，因为视差太小导致深度无法被可靠估计的点），使用了逆深度来表示远点。经验上，如果点的深度小于双目基线的40倍，那么这些点可以被可靠的三角化。
• 用滑窗可以实现BA的常数时间复杂度，但是不能保证全局一致性（？）。对于ORB-SLAM2，自局部的关键帧使用BA来保证时间复杂度与map大小无关；在回环时，系统先对其两边，所以追踪可以继续用老地图定位，然后用全局BA来实现位姿图优化来最小化累计漂移。

RGB-D SLAM

• ORB-SLAM2使用深度信息来给图像上提取出的特征点合成双目坐标。这样双目和rgb-d的输入的之后处理其实就可以统一了。ORB-SLAM2这里的后端用的是BA，也建立了一个全局一致的稀疏重建。因为目的就是长时间和全局一致的定位，而不是为了有很多细节的稠密重建。但是在有了很准的关键帧位姿之后，就可以融合深度地图和得到局部准确的重建；或者是在全局BA后，后处理由所有关键帧构成的深度地图，得到整个场景的准确的3D模型。

III.ORB-SLAM2

扩充传感器之后，整体的流程图为：
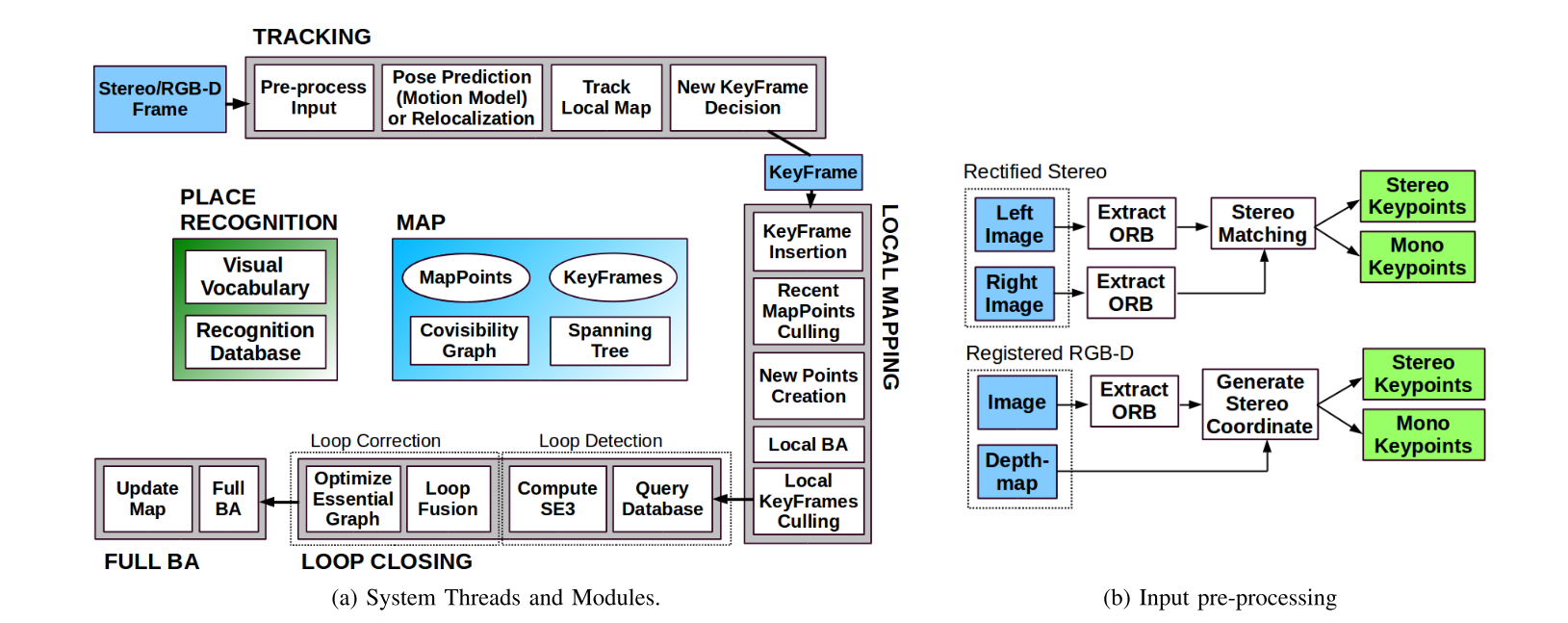1. 三个平行的主线程是：
1）追踪：每一帧都去找和局部地图的特征匹配来定位相机，并使用motion only BA来最小化重投影误差。
2）局部建图：管理局部地图并优化，使用局部BA
3）回环：检测大回环，通过位姿图优化修正累计漂移（~）。这个线程还启动了第四个线程在位姿图优化之后进行全局BA。
2. 需要用到重定位的场合：

• 追踪失效（如遮挡）
• 重初始化（在已经建图过的场景）
• 回环检测

A. Monocular, Close Stereo and Far Stereo Keypoints

从前面的流程图可以看到，后续双目和rgbd其实是没有区别的。所以这里重点说双目关键点和单目关键点。

双目关键点

双目关键点的深度如果小于40倍基线长度的值，就被叫做近关键点，否则就是远关键点。近关键点可以较好的被三角化，并提供尺度，平移，旋转信息。而远关键点可以提供比较好的旋转信息，但只能有比较差的尺度和平移信息，远点用多视角进行三角化。
定义： 用(uL,vL,uR)(u_L, v_L, u_R)(uL​,vL​,uR​)表示。前两个就是在左图像的特征点坐标，uRu_RuR​是在右图像匹配特征点的水平坐标。对于双目相机，利用双目的校正后图像进行搜索（此时极线水平，搜索很快）。对于RGB-D相机，就计算出一个虚拟的右坐标：
uR=uL−fxbdu_R = u_L - \frac{f_xb}{d}uR​=uL​−dfx​b​
fxf_xfx​是水平焦距，b是结构光投影和红外线相机的基线，深度传感器的不确定度就是用虚拟右坐标的不确定度表示。

单目关键点

定义： 对于ORB特征点中，那些没有对应双目匹配的，或者是没有有效深度值的特征点，取他们在左图像中的点坐标作为单目关键点，即(uL,vL)(u_L, v_L)(uL​,vL​)。
如何三角化： 只能通过多视角三角化，不提供尺度信息，只提供旋转和平移估计。

B. System Bootstrapping

不需要像单目那样进行系统初始化了。第一帧时就可以创建一个关键帧，把它的pose设置到起点，从所有双目关键点创建出一个初始地图。

C. Bundle Adjustment with Monocular and Stereo Constraints

追踪线程：用BA优化相机位姿（motion only BA）
局部建图线程：局部BA，优化一个局部窗口内的关键帧和点
闭环之后：全局BA，优化所有关键帧和点
使用的是g2o的LM方法

Motion-only BA

最小化匹配的世界坐标系3D点Xi∈R3X^i \in \mathbb R^3Xi∈R3和关键点x(⋅)ix^i_{(·)}x(⋅)i​之间的重投影误差。对于单目关键点xmi∈R2x_m^i \in \mathbb R^2xmi​∈R2或者双目关键点xsi∈R3x^i_s \in \mathbb R^3xsi​∈R3, 都满足下面的式子：
{R,t}=arg⁡min⁡R,t∑ρ(∥x(⋅)i−π(⋅)(RXi+t)∥∑2)\{ R,t \} = \mathop{\arg\min_{R,t}} \sum \rho (\Vert x^i_{(·)} - \pi_{(·)}(RX^i + t) \Vert _{\sum} ^2){R,t}=argR,tmin​∑ρ(∥x(⋅)i​−π(⋅)​(RXi+t)∥∑2​)
这里的i就是所有匹配集合中的某一个；$\rho$就是鲁棒的Huber cost function；$\sum$是关键点尺度相关的协方差矩阵；对于投影方程π(⋅)\pi_{(·)}π(⋅)​，单目和双目的都有各自的定义：

πm([XYZ])=[fxXZ+cxfyYZ+cy],πs([XYZ])=[fxXZ+cxfyYZ+cyfxX−bZ+cx]\pi_m(\begin{bmatrix} X\\ Y\\ Z\\ \end{bmatrix}) = \begin{bmatrix} f_x \frac{X}{Z} + c_x\\ f_y \frac{Y}{Z} + c_y\\ \end{bmatrix}, \pi_s(\begin{bmatrix} X\\ Y\\ Z\\ \end{bmatrix}) = \begin{bmatrix} f_x \frac{X}{Z} + c_x\\ f_y \frac{Y}{Z} + c_y\\ f_x \frac{X-b}{Z} + c_x\\\end{bmatrix}πm​(⎣⎡​XYZ​⎦⎤​)=[fx​ZX​+cx​fy​ZY​+cy​​],πs​(⎣⎡​XYZ​⎦⎤​)=⎣⎡​fx​ZX​+cx​fy​ZY​+cy​fx​ZX−b​+cx​​⎦⎤​

Local BA

优化共视的关键帧KLK_LKL​和这些关键帧中的所有点PLP_LPL​。那些没有共视的关键帧KFK_FKF​，其中被观察到的PLP_LPL​对cost函数有贡献，但是在优化过程中保持不变（？？）。定义χk\chi_kχk​是在PLP_LPL​中的点和一个关键帧k中关键点之间的匹配集合，优化问题如下：
{Xi,Rl,tl∣i∈PL,l∈KL}=arg min⁡Xi,Rl,tl∑k∈KL∪KF∑j∈χkρ(Ekj)Ekj=∥x(⋅)i−π(⋅)(RkXj+tk)∥∑2\{X^i, R_l, t_l \vert i \in P_L, l \in K_L\} = \mathop{\argmin_{X^i, R_l, t_l} \sum_{k\in K_L \cup K_F} \sum_{j \in \chi_k}\rho (E_{kj})} \\E_{kj} = \Vert x^i_{(·)} - \pi_{(·)}(R_kX^j + t_k) \Vert _{\sum} ^2{Xi,Rl​,tl​∣i∈PL​,l∈KL​}=Xi,Rl​,tl​argmin​k∈KL​∪KF​∑​j∈χk​∑​ρ(Ekj​)Ekj​=∥x(⋅)i​−π(⋅)​(Rk​Xj+tk​)∥∑2​

Full BA

这个就是Local BA的特例，此时所有的关键帧和地图中的所有点都会被优化，除了被固定的初始关键帧（固定是为了消除gauge freedom）。

D. Loop Closing and Full BA

对于双目和rgbd的情况，不会有尺度漂移，而且双目或者深度信息是基于刚体转换的而不是相似度（~）。
在 ORB-SLAM2 中，在位姿图之后加入了完整的 BA 优化以实现最佳解决方案。这种优化可能很耗时，所以在单独的线程中执行，这样就可以让系统继续创建地图和检测回环。但是，这让BA输出和地图当前状态的合并造成了困难。

• 如果在优化运行时检测到新回环，将中止优化并继续闭环，这将再次启动完整的 BA 优化。
• 当全局 BA 完成时，需要将更新的关键帧子集和由全局BA优化的点与 未更新的关键帧和在优化运行时插入的点合并（~）。这是通过将更新的关键帧的校正（即从未优化到优化的姿势的转换）通过生成树传播到未更新的关键帧来完成的。未更新的点根据应用于其参考关键帧的校正进行变换。 （~）

E. Keyframe Insertion

和单目的一样，都是尽可能多的加入关键帧，然后再去掉冗余的关键帧。
但考虑到近关键点和远关键点，这里还引入了一个新的条件：如果跟踪的近点的数量小于阈值τt\tau_tτt​且这一帧可以创造至少τc\tau_cτc​个近双目点，那么就插入一个新关键帧。经验值τt=100，τc=70\tau_t=100， \tau_c=70τt​=100，τc​=70

F. Localization Mode

局部建图和回环线程是不激活的，只有追踪线程工作，而追踪线程使用视觉里程计匹配和地图点匹配。

• 视觉里程计匹配：当前帧ORB特征点和之前帧从双目或深度信息得来的3D点的匹配。这种匹配可以对没有建图的区域能鲁棒的定位，但是有累计的漂移。
• 地图点匹配：对现存地图的无漂移的定位

IV. EVALUATION

对于kitti的01序列（高速公路场景）来说，平移的结果是比较不好的，原因就是能被追踪的近点太少了（汽车高速运动，而相机低帧率），但角度还是能估计的比较准。和单目相比，双目的效果更好，一是因为近点更好追踪，因为从一个双目关键帧就可以创建点，而不用像单目那样弄延迟的初始化（要在俩关键帧之间匹配），双目的情况更不容易出现track lost；二是双目可以带尺度的估计地图和轨迹，没有轨迹漂移。（可以明显看出左边图中，路程后段的尺度漂移）

对于EuRoC数据集，由于严重的运动模糊会使track lost出现。论文提到的一个解决办法是使用imu信息，之前在github看到有人提到的一个解决办法是，把track lost部分的图像进行锐化的预处理（没有证实过是否有效）

对于时效性。回环中关键帧的数量就可以对应出回环的耗时。关键帧越多，共视图就会越密集，回环的融合，位姿优化，全局BA也就会更加耗时。高密度的共视图会让局部地图包含更多关键帧和点，因此局部地图的追踪和局部BA会更耗时。