连续系统的动态特性通常可以通过一个或一组微分方程来描述。为了对这些系统进行仿真,需要对微分方程进行数值求解。数值积分方法是常用的技术手段,其中最典型的两种方法是欧拉法和龙格-库塔法。
设有一个微分方程如下: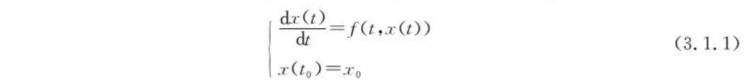
数值积分的目标是在定义域区间内找到若干个离散点的近似解,并将其相加。这就是欧拉法和龙格-库塔法的基本思想。
欧拉法的核心思想是将积分曲线用折线近似表示。具体步骤如下:
1. 计算某一点的导数,乘以一定的步长,再加上前一个点的值,得到下一个点的值。
2. 重复上述过程,直到求出所有点的值。
优点:
- 方法简单,计算量小。
缺点:
- 精度较低,但可以通过减小步长来改善。
龙格-库塔法基于泰勒级数展开,通过间接使用泰勒公式来提高计算精度。具体步骤如下:
1. 使用泰勒级数确定系数,然后乘以各阶导数的函数值。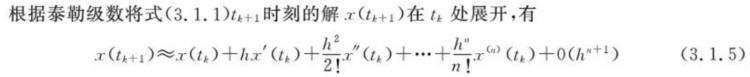
2. 四阶龙格-库塔法在实际应用中具有较高的精度,其递推公式如下: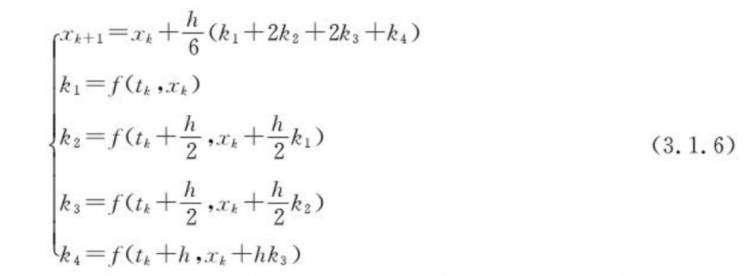
简而言之,欧拉法和龙格-库塔法的主要区别在于迭代时使用的公式不同。欧拉法仅使用一阶导数,而龙格-库塔法使用多阶导数,因此计算更加精确。
下面是一个使用MATLAB实现欧拉法和龙格-库塔法求解SISO系统输出的例子。
首先,将传递函数转换为状态空间方程,然后进行求解。
% 欧拉法与龙格-库塔法的比较
clear all;
close all;
clc;
% 欧拉法的计算步长
h = 0.3;
% 仿真步数
L = 15 / h;
% SISO对象的零极点型
z = [-1 -2];
p = [-4 -0.5+j -0.5-j];
k = 2.5;
% 转换成状态空间
[A, B, C, D] = zp2ss(z, p, k);
% 输入和初值
u = 1 * ones(L, 1);
u0 = 0;
% 对象的阶次
n = length(p);
% 龙格-库塔和欧拉的状态初值
xrk0 = zeros(n, 1); % 3*1
xer0 = zeros(n, 1);
for i = 1:L
time(i) = i * h;
% 欧拉法,更新单步
xer = xer0 + h * (A * xer0 + B * u0);
yer(i) = C * xer;
% 更新数据,将当前值作为初值,便于下一次更新
xer0 = xer;
u0 = u(i);
end
for i = 1:L
time(i) = i * h;
% 龙格-库塔法迭代公式
k1 = A * xrk0 + B * u0;
k2 = A * (xrk0 + h * k1 / 2) + B * u0;
k3 = A * (xrk0 + h * k2 / 2) + B * u0;
k4 = A * (xrk0 + h * k3) + B * u(i);
xrk = xrk0 + h * (k1 + 2 * k2 + 2 * k3 + k4) / 6;
yrk(i) = C * xrk;
% 更新数据
xrk0 = xrk;
u0 = u(i);
end
plot(time, yer, 'b', time, yrk, 'r');
legend('Euler', 'Runge-Kutta');蓝色线条表示欧拉法的计算结果,红色线条表示龙格-库塔法的计算结果。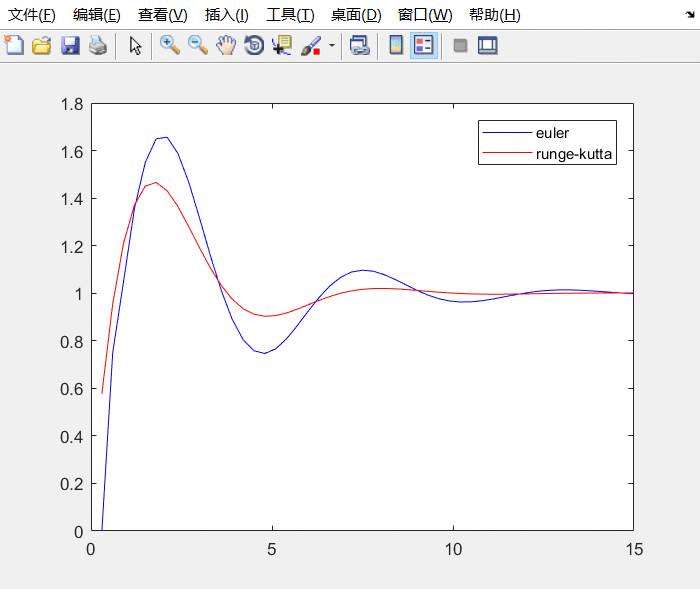
适当提高精度,将步长h调整为0.1,可以看到欧拉法的精度显著提高,但在一定时间后,两种方法的结果趋于一致。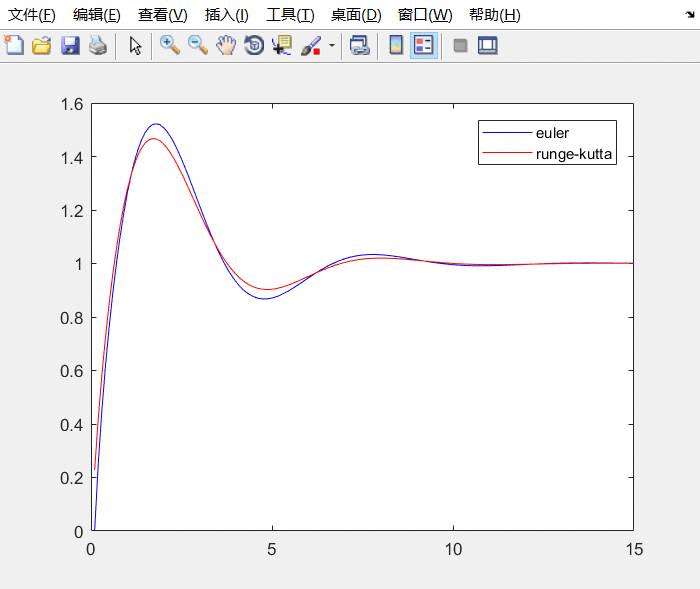

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有