下面这张图片是从网络上拷贝过来,以这张图片为模型,我们来一步一步论证推导两轮差速运动模型,以下是原来网络上对这张图片的描述。
下图是移动机器人在两个相邻时刻的位姿,其中 是两相邻时刻移动机器人绕圆弧运动的角度, 是两相邻时刻移动机器航向角(朝向角head)的变化量。 是左右轮之间的间距, 是右轮比左轮多走的距离。 是移动机器人圆弧运动的半径。
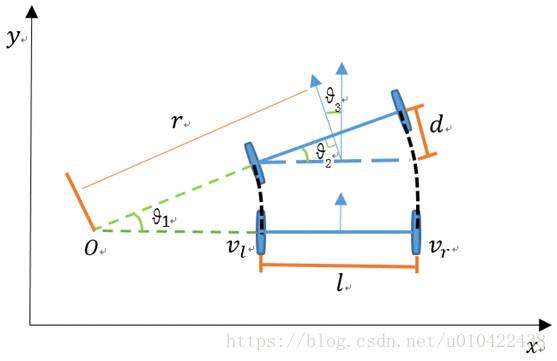
从以上描述中我们得到一些定义:
网络描述中d的定义有些狭隘,我们不使用它的定义,使用一些新的定义。按照常理,两轮子顺时针旋转,小车前进,两轮子逆时针旋转,小车后退,我们按照这个习惯,定义轮子顺时针为正方向,逆时针为负方向。同时我们定义初始状态下,距离原点最近的轮子为左轮,另外一个轮子为右轮
定义θ为X轴单位向量旋转θ角度后跟向量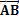 平行所得,以逆时针旋转为正方向,则
平行所得,以逆时针旋转为正方向,则
由几何关系分析可知:任意时刻
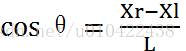
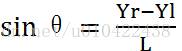
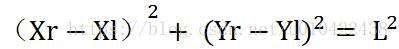
定义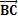 为B点的速度,同理定义β为X轴单位向量旋转β角度后跟向量
为B点的速度,同理定义β为X轴单位向量旋转β角度后跟向量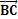 平行所得,以逆时针旋转为正方向,因为任意时刻
平行所得,以逆时针旋转为正方向,因为任意时刻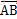 ⊥
⊥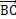 则,已知B点角速度为ω1,由几何关系分析可知:任意时刻
则,已知B点角速度为ω1,由几何关系分析可知:任意时刻
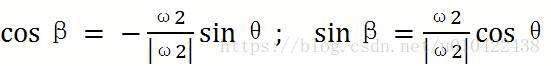
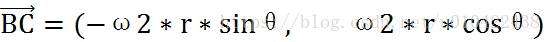
定义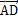 为A点的速度,同理定义Ф为X轴单位向量旋转Ф角度后跟向量
为A点的速度,同理定义Ф为X轴单位向量旋转Ф角度后跟向量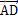 平行所得,同理
平行所得,同理
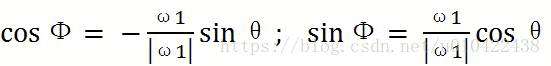
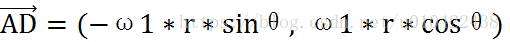
由于点M(x,y)为线段AB中点,所以m点速度为
Vm = (V1+ V2)/2 = ( -(ω1+ω2)*r* sinθ), (ω1+ω2)*r* cosθ)
假定在时刻t,左轮角速度为ωt1,右轮角速度为ωt2,经过时间Δt,当Δt→0时有:
因为任意时刻,两轮子的速度方向平行于同一直线,所以,M点线速度
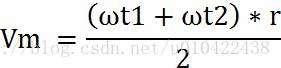
左轮的运动弧长
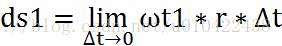
右轮的运动弧长
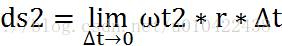
由几何学分析我们可以得到,向量AB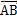 与X轴单位向量的夹角θ的增量
与X轴单位向量的夹角θ的增量
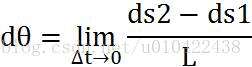
由几何学分析已知,向量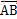 与X轴单位向量的夹角θ的增量与航向角的增量任意时刻都相等相等,所以,t时刻,M点角速度为
与X轴单位向量的夹角θ的增量与航向角的增量任意时刻都相等相等,所以,t时刻,M点角速度为
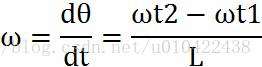
所以,时刻t,M点运动半径
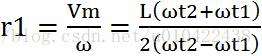
假定M点初始坐标为(a,b),初始状态下X轴单位向量旋转β角度后与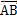 平行,则
平行,则
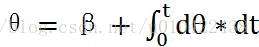
M点轨迹参数方程为,
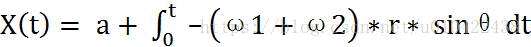
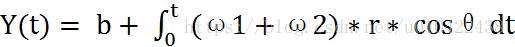

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有