扩散过程与完备市场

Girsanov定理

考虑布朗运动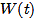&＃xff0c;如果定义新过程

则在由RN导数过程

诱导的测度变换下&＃xff0c;是下的鞅。

证明思路&＃xff1a;

&＃xff08;1&＃xff09;利用Ito引理证明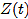是鞅

&＃xff08;2&＃xff09;证明&＃xff0c;从而是一个RN导数过程

&＃xff08;3&＃xff09;证明是鞅

&＃xff08;4&＃xff09;证明是下的鞅

&＃xff08;5&＃xff09;证明&＃xff0c;再由Levy定理证明结论。

可以将之扩展到多维&＃xff0c;即&＃xff0c;如果有独立布朗运动的变换&＃xff0c;其中&＃xff0c;每一个的变换与一维情形一样&＃xff0c;则相应的RN过程为

扩散过程下的完备市场

假设市场由个自由度的布朗运动驱动&＃xff0c;市场上有种可交易资产&＃xff0c;则其扩散微分方程为

坐标变换&＃xff0c;定义新的维布朗运动

其中

在为常数时就是线性变换&＃xff0c;这时为相关&＃xff0c;满足

这时我们观测到的市场是

回到开始的模型&＃xff0c;我们希望找到风险中性测度&＃xff0c;利用Girsanov定理&＃xff0c;我们希望定义新的布朗运动

代入后得到

要使得在这个变换得到的测度下为鞅&＃xff0c;我们要求    

矩阵形式为

如果此方程有解&＃xff0c;则存在风险中性测度&＃xff0c;如果无解&＃xff0c;则市场存在套利。如果存在唯一解&＃xff0c;则市场为完备市场。

唯一解条件为且

以二维条件为例&＃xff0c;如果我们知道及&＃xff0c;则

还剩下一个自由度可选&＃xff0c;这实际上表明我们的独立化方法并不唯一。这并不奇怪&＃xff0c;也不是什么大问题。考虑联合标准正态变量&＃xff0c;相关系数为&＃xff0c;我们希望找到线性变换&＃xff0c;使其成为新的独立的标准正态变量&＃xff0c;有

其中&＃xff0c;限制条件为

满足上式的均符合要求。通常可以选择&＃xff0c;从而取&＃xff0c;第三式成为

和第二式联立&＃xff0c;立马得到&＃xff0c;&＃xff0c;因此

也就是说&＃xff0c;回到原来的问题&＃xff0c;可以以一个为基准&＃xff0c;令&＃xff0c;然后通过限制条件得到一组独立化的。从而得到矩阵&＃xff0c;解出&＃xff0c;最后求出这个市场的风险中性测度。

考虑如果市场无套利&＃xff0c;则鞅测度存在&＃xff0c;因此从任意一个未定权益出发可以构造一个鞅为

由表示定理我们必然有

而财富过程必须满足

然而如前所述我们知道

我们发现只需要取满足方程

如果风险中性测度是唯一的&＃xff0c;即

有唯一解&＃xff0c;这意味着对应的齐次方程只有零解。从而方程有至少一个解。于是我们得到

有解&＃xff0c;因此是存在的&＃xff0c;故而任意一个未定权益都可以得到对冲。

我们处理得最多的还是的情形&＃xff0c;这时&＃xff0c;我们有风险中性定价公式

或者写成

相应的股价服从

考虑比几何布朗运动更General的情形&＃xff0c;在和非随机时其解为

对于是的函数的情形&＃xff0c;我们要计算只需要求出在下的分布即可&＃xff0c;为此&＃xff0c;定义平均波动率和平均利率为

于是有

从而对Call Option有

直接计算可以得到

其中

因此第一项积分可以表示为

我们令便得到所谓的方程

当为一个远期时我们立马可以得到

于是利用我们得到期权平价关系

由此立马可以得到put option的价格

这意味着存在上限&＃xff0c;故可以小于Intrinsic Value。

光有价格还不行&＃xff0c;我们还需要求出来的是对冲策略。如果是一个的&＃xff0c;这意味着欧式未定权益的期望可以表示成现值的函数。于是&＃xff0c;这允许我们使用引理。于是

由于是鞅&＃xff0c;我们立马得到微分方程

另一方面&＃xff0c;注意到鞅性&＃xff0c;丢弃所有的项得到

但是我们已经有

比较两式便得到对冲策略

导数与风险参数&＃xff08;Greeks&＃xff09;

在计算导数与风险参数的时候&＃xff0c;一些结论是反复用到的

&＃xff08;1&＃xff09;

&＃xff08;2&＃xff09;

&＃xff08;3&＃xff09;

&＃xff08;4&＃xff09;

&＃xff08;5&＃xff09;

&＃xff08;6&＃xff09;

&＃xff08;7&＃xff09;

我们计算所有的导数&＃xff1a;

Delta:

而

因此

一个重要结论为

Gamma:

满足期权的凸性不等式。此外我们可以看到。

对求一阶微分会发现极大值点出现在即处。

Vega:

Theta&＃xff1a;

因此

故put的Theta不一定为负。

Rho:

这可以从支付函数上直接看出来