控制系统分析与设计（二）：比例积分控制器的传递函数

1. 理想运算放大器的特点：

（1）无限大的输入阻抗：理想运算放大器输入端不允许电流输入，i₊=i_&＃8211;=0
（2）趋于零的输出阻抗：理想运算放大器的输出端是一个完美的电压源，无论流至放大器负载的电流如何变化，放大器的输出电压恒为定值，
（3）电压放大倍数A趋于无穷大：u₊=u_&＃8211;
输出电压u_o与同向端输入电压u₊、反向端输入电压u_&＃8211;及电压放大倍数A的固有关系为
u o = A ( u + − u − ) u_o=A(u_+-u_-) uo​=A(u+​−u−​)
( u + − u − ) = u o A (u_+-u_-)=\frac {u_o}{A} (u+​−u−​)=Auo​​
因为A趋向于无穷大，u_o局限于有限的电压范围内，则
u + − u − → 0 u_+-u_- \to 0 u+​−u−​→0
即 u + ≈ u − u_+ \approx u_- u+​≈u−​

2. 比例积分控制器传递函数求解示例

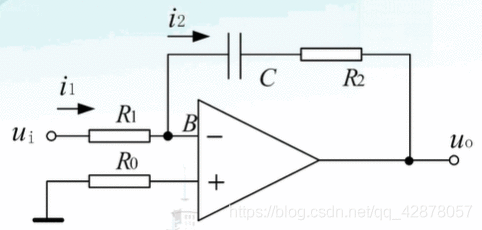
基于以上特点可以得到u₊=u_&＃8211;=0V，i₁=i₂，可以在分析时将理想运算放大器去掉：

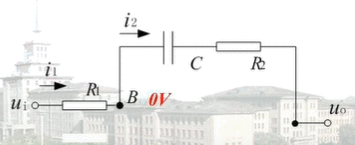
此时求比例积分控制器的传递函数：
{ U i ( s ) − 0 = I 1 ( s ) ∗ R 1 0 − U o ( s ) = I 2 ( s ) ∗ ( R 2 + 1 C s ) \left\{ \begin{array}{l} U_i(s)-0=I_1(s)*R_1 \\ 0-U_o(s)=I_2(s)*(R_2+\frac 1{Cs}) \end{array} \right. { Ui​(s)−0=I1​(s)∗R1​0−Uo​(s)=I2​(s)∗(R2​+Cs1​)​
则
G ( s ) = U o ( s ) U i ( s ) = − I 2 ( s ) ∗ Z 2 I 1 ( s ) ∗ Z 1 = − Z 2 Z 1 = R 2 C s + 1 R 1 C s G(s)=\frac {U_o(s)}{U_i(s)}=\frac {-I_2(s)*Z_2}{I_1(s)*Z_1}=-\frac {Z_2}{Z_1}=\frac{R_2Cs+1}{R_1Cs} G(s)=Ui​(s)Uo​(s)​=I1​(s)∗Z1​−I2​(s)∗Z2​​=−Z1​Z2​​=R1​CsR2​Cs+1​
在其他一些涉及理想运算放大器的传递函数求解均可以对电路进行先化简再求解！