开发笔记:图像识别基于ORL数据库的PCA人脸识别系统matlab源码

1. PCA人脸识别操作流程

    在平时的研究中&＃xff0c;我总结的PCA人脸识别的主要流程如下图所示&＃xff1a;

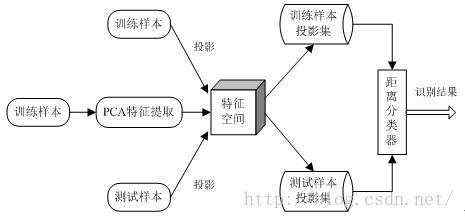
                                                    图 1 PCA人脸识别流程图

      通过上图的PCA人脸识别流程可以看出&＃xff0c;PCA方法可以总结为以下几个阶段&＃xff1a;训练样本、特征提取、构造特征空间、投影计算。

2. PCA人脸识别方法原理介绍

       Karhunen-Loeve(K-L)变换或主要分量分析(Principal Component Analysis&＃xff0c;PCA)是普遍使用的一种技术,这种技术的主要作用是将续信号转换为一组不相关的表示系数。主要分量分析(PCA)形成了K-L变换的基础&＃xff0c;主要用于数据的紧凑表示。在数据挖掘的应用中&＃xff0c;它主要应用于简化大维数的数据集合&＃xff0c;减少特征空间维数&＃xff0c;可以用较小的存储代价和计算复杂度获得较高的准确性。

    PCA方法通过消除数据的相关性&＃xff0c;找到一个空间&＃xff0c;使得各个类别的数据在该空间上能够很好地分离。如下图所示&＃xff1a;

                                                  图 2 PCA降维和分类示意图

在图2中&＃xff0c;有一些离散的二维分布点&＃xff0c;其中五角星表示一类集合&＃xff0c;小圆圈表示另一类集合&＃xff0c;假设这两个类别可以用特征X和特征Y进行描述&＃xff0c;由图可知&＃xff0c;在X轴和Y轴上这两个类别的投影是重叠的&＃xff0c;表明这些点的两个特征X和Y没有表现出突出的识别性。但是两个类的投影在Z轴上区分度较大&＃xff0c;显示出很好的识别性。PCA就是这样的一个工具&＃xff0c;它可以产生非常好的降维效果&＃xff0c;这种方法也可以用在图像处理的其他的一些研究中&＃xff0c;如图像压缩、分类以及特征选择等。

    接下来详细介绍一下PCA的理论原理&＃xff1a;

    通过对主成分分析方法做了简单的说明以后&＃xff0c;接下来&＃xff0c;我们来具体分析一下K-L变换的原理。

    假设在图像集合f(m,n)中&＃xff0c;每张图像可以用堆叠的方式表示成一个维列向量&＃xff1a;

                            　　　　　　　  (1)

其表示方法为&＃xff1a;从图像矩阵的第一列开始取&＃xff0c;依次取到最后一列&＃xff0c;每一列首尾相连&＃xff0c;构成一个维列向量。将每一幅人脸图像表示

列向量以后&＃xff0c;然后依次将每一个图像列向量转置成行向量&＃xff0c;构成一个人脸样本矩阵&＃xff0c;该样本矩阵即图像集合&＃xff1a;

                                                     (2)

由式(2)可知样本矩阵有L行&＃xff0c;其中每一行的数据就代表一张人脸样本图像&＃xff0c;L表示训练样本的总个数。  

训练样本的协方差矩阵为&＃xff1a;

                              　　　　　　　　　　　　                                           (3)

式中mf是所有训练样本的平均值向量&＃xff0c;也即是所有样本的平均脸。(3)式中的[Cf]阵为阶实对称方阵&＃xff0c;则其一定存在个相互正交的属于各个特征值的特征向量&＃xff0c;即有&＃xff1a;

                          　　　                                             　 (4)

将上述特征值进行降序排列&＃xff0c;并取每个特征值对应的特征向量构成一个正交矩阵&＃xff0c;也即是一个维的正交空间。按照文献中的说明&＃xff0c;此处的矩阵[Cf]的维数很大&＃xff0c;求解其特征值和特征向量比较复杂&＃xff0c;这个时候需要对&＃xff08;3&＃xff09;式进行变形&＃xff0c;简化求解&＃xff0c;其变形结果如下&＃xff1a;

                     　　　　　　　　　　　　　　                                      (5)

此时&＃xff0c;对&＃xff08;5&＃xff09;式中的矩阵进行特征值和特征向量的求解&＃xff0c;将求解出的特征向量和特征值经过SVD奇异值分解&＃xff0c;得到原训练样本的特征向量&＃xff0c;这样就可以构造出最终的人脸投影空间。

                    　　　　　　　　　　　                              &＃xff08;6&＃xff09;

其中vi就是&＃xff08;5&＃xff09;中协方差矩阵的特征向量&＃xff0c;&＃xff50;是特征向量的个数。将特征向量转化为矩阵&＃xff0c;矩阵就可以表示图像&＃xff0c;也即是所谓的特征脸&＃xff0c;如下&＃xff1a;

                                              图 3 PCA特征脸

到这里为止&＃xff0c;我们就找到了PCA人脸识别需要的投影特征空间了&＃xff1a;

　　　　　　　　　　　　　　　　　　&＃xff08;&＃xff17;&＃xff09;

接下来就可以通过&＃xff2b;&＃xff0d;&＃xff2c;变换式进行投影计算了&＃xff0c;得出各个样本在空间Wpca上的投影特征了&＃xff1a;

                                           　　　　　                                 　　　　　　　　　　       &＃xff08;8&＃xff09;

其中&＃xff3b;A&＃xff3d;就是空间Wpca&＃xff0c;其实&＃xff08;8&＃xff09;式中不用&＃xff08;f-mf&＃xff09;也行&＃xff0c;直接换成f就可以&＃xff0c;即表示将原人脸样本在空间Wpca上进行投影&＃xff0c;将投影后的特征系数存在矩阵g中&＃xff0c;如果没有记错的话&＃xff0c;g中每一行表示一个人脸样本的特征系数&＃xff08;或者每一列表示一个人脸样本的特征稀疏&＃xff0c;这个与个人的计算方法有关&＃xff0c;主要是看矩阵的转置或者不转置&＃xff09;。

    到这里PCA人脸识别的主要步骤已经介绍完了&＃xff0c;剩下的就是识别过程了&＃xff0c;这个比较容易理解&＃xff0c;首先将训练样本在空间[A]上进行投影&＃xff0c;得到投影样本的特征系数&＃xff0c;然后将测试样本也在空间[A]上进行投影&＃xff0c;得到每个测试杨样本的投影特征系数&＃xff0c;此时&＃xff0c;只需将测试某个样本的特征系数与训练样本投影特征系数进行欧式距离度量&＃xff0c;看要测试的那个样本与训练集中哪个样本的欧式距离最近&＃xff0c;就可以将该测试样本归为与之距离最近那个样本的类别。比如&＃xff1a;训练样本a1属于S1类&＃xff08;S1类中包含很多样本&＃xff0c;a1只是其中的一个样本&＃xff09;&＃xff0c;如果测试样本b1和a1的距离最近&＃xff0c;那么就将b1归为S1类。如此下来&＃xff0c;对所有的样本进行分类&＃xff0c;就可以得到PCA人脸识别率了。



%测试数据&＃xff1a;40人&＃xff0c;每人10张照片。每人取前train_num张照片作为训练集&＃xff0c;后&＃xff08;10&＃xff0d;train_num&＃xff09;张照片作为测试集。
clear all;
clc;
train_num&＃61;5;

%计算特征脸并创建特征空间
imdata&＃61;zeros(112*92,40*train_num);
for i&＃61;1:40
for j&＃61;1:train_num
addr&＃61;strcat(&＃39;Dum2str(j),&＃39;.bmp&＃39;);
a&＃61;imread(addr);%从地址中读入图像
b&＃61;a(1:112*92); %把图像a矩阵按列顺序转为行向量b
imdata(:,train_num*(i-1)&＃43;j)&＃61;b&＃39;; %把b的转置矩阵存放到imdata矩阵的第ph*(i-1)&＃43;j列
end
end
[neednum,average_face, immin, newVT] &＃61; newVT(imdata);
OutputClass &＃61; Recognition(&＃39;\\FaceRecognitionPCA\\faces\\s29\\6.bmp&＃39;,neednum,average_face, immin,newVT)

完整代码或者仿真咨询添加QQ1575304183