本文涉及：cdq分治、MST

一道十分精妙的cdq分治题(o゜▽゜)o。据说线段树分治+LCQ维护MST也是一种解法，但我并不会...

1 题意

给定一个(n)个点，(m)条边的无向带边权的图，和(q)次询问；每一次询问会修改一条边的边权；在每一次询问后求出当前图的最小生成树的权值。

数据范围：(nleq2000,m,qleq 5000)

2 解法

这道题的暴力十分显然，固不再赘述。

设函数(solve(l,r))，表示处理修改序列([l,r])中的修改；动态边表示与修改序([l,r])中的修改有关的边；反之，静态边表示与这段修改无关的边。

对于动态边我们暂且不加以考虑，因为随着函数的递归运行，动态边将不断地变化为静态边；反观静态边，它们从定为静态边起身份就不再发生改变。因为我们接下来将着重讨论如何通过必选边和无用边的划分，简化静态边边集。

必选边：将动态边的边权设为(-infty),求一次MST，此时MST中除边权为(-infty)外的边都是必选边

将一条边设为(-infty)，在MST中就会优先考虑这条边。动态边都被设为了(-infty)，但仍然有静态边被选中，说明动态边集不能保证图的连通，只有依赖这些静态边，图才能是连通的。根据MST的选取规则，选中的这些静态边又是所有可行方案中最优的，因此是必选边

对于必选边，将边的两个端点缩在一起后，累加边权。

无用边：将动态边的边权设为(infty)，求一次MST，此时没有出现在MST中的静态边是无用边

相比必选边，此时动态边的地位一落千丈。此时没有被选中的静态边在动态边边权恢复正常后更加不可能被选上，因此是无用边。

对于无用边嘛，丢了就好╰(￣ω￣ｏ)

对于某一函数([l,r])，其递归函数([l,mid])和([mid+1,r])的静态边集必包含了它自身的静态边集，因此不会因为简化当前边集而出错。

每层分治时，用上述两种方法缩小图的规模；在最后一层使修改生效，求一遍MST和累加值求和即是答案。此时图的规模已经不大，可以放心kruskal。

因为分治的顺序，在处理([l,r])时，区间([1,l-1])中的修改已被落实，如下图：

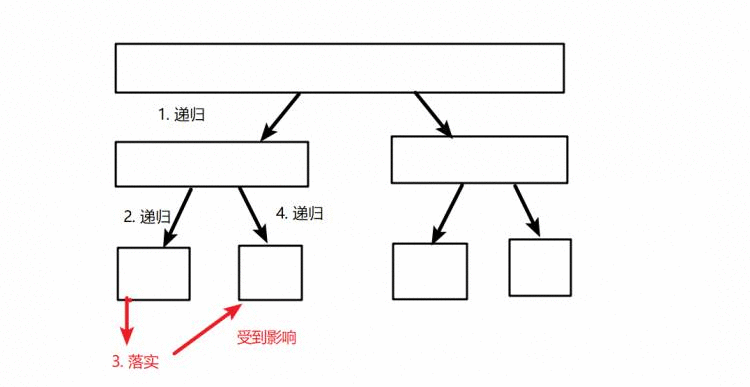
这一点是我当时的理解难点

3 代码

#include
using namespace std;
#define lor(a,b,c) for(register int a=b;a<=c;++a)
#define ror(a,b,c) for(register int a=c;a>=b;--a)
typedef long long ll;
const int MAXN=2e4+5,MAXM=5e4+5,MAXD=17;
const ll INF=5e10+5;
int n,m,q; int qid[MAXM]; ll qval[MAXM];
ll ans[MAXM]; bool ban[MAXM];
struct data{
int x,y,id; ll z,bac;
inline bool operator <(data b) const{
return z }
}info[MAXM],work[MAXD][MAXM],up[MAXM];
inline bool cmpf(data a,data b) {return ban[a.id]==ban[b.id]?a.zban[b.id];}
inline bool cmpb(data a,data b) {return ban[a.id]==ban[b.id]?a.zint fat[MAXN]; bool vis[MAXM];
inline void clear() {lor(i,1,n) fat[i]=i;}
inline int find(int a) {while(a^fat[a]) a=fat[a]=fat[fat[a]]; return a;}
inline bool unionn(int a,int b) {int aa=find(a),bb=find(b); return aa==bb?(false):(fat[aa]=bb,true);}
void cdq(int,int,int,int,ll);
inline ll vital(int,int,int,int&);
inline void radish(int,int,int,int&);
int main(){
#ifndef ONLINE_JUDGE
freopen("test.in","r",stdin);
freopen("test.out","w",stdout);
#endif
scanf("%d%d%d",&n,&m,&q);
lor(i,1,m) scanf("%d%d%lld",&info[i].x,&info[i].y,&info[i].z),info[i].id=i;
lor(i,1,q) scanf("%d%lld",&qid[i],&qval[i]);
lor(i,1,m) work[0][i]=info[i];
cdq(1,1,q,m,0);
lor(i,1,q) printf("%lld
",ans[i]);
return 0;
}
void cdq(int dep,int l,int r,int s,ll v){
if(l==r) {info[qid[l]].z=qval[l];}
lor(i,1,s) {work[dep][i]=work[dep-1][i]; work[dep][i].z=info[work[dep][i].id].z;}
if(l==r){
ans[l]=v; clear();
sort(work[dep]+1,work[dep]+1+s);
lor(i,1,s) if(unionn(work[dep][i].x,work[dep][i].y)) ans[l]+=work[dep][i].z;
return;
}
v+=vital(dep,l,r,s);
radish(dep,l,r,s);
int mid=(l+r)>>1; cdq(dep+1,l,mid,s,v); cdq(dep+1,mid+1,r,s,v);
}
inline ll vital(int dep,int l,int r,int &s){
lor(i,l,r) ban[qid[i]]=true;
ll ans=0; int tmp=0; lor(i,1,s) vis[i]=false;
sort(work[dep]+1,work[dep]+1+s,cmpf);
lor(i,1,s){
if(unionn(work[dep][i].x,work[dep][i].y)) vis[i]=true;
}
lor(i,1,s){
fat[work[dep][i].x]=work[dep][i].x; fat[work[dep][i].y]=work[dep][i].y;
}
lor(i,1,s) if(!ban[work[dep][i].id]&&vis[i]){
unionn(work[dep][i].x,work[dep][i].y); ans+=work[dep][i].z;
}
lor(i,1,s){
if(ban[work[dep][i].id]||!vis[i]){
work[dep][i].x=find(work[dep][i].x); work[dep][i].y=find(work[dep][i].y);
up[++tmp]=work[dep][i];
}
}
lor(i,1,s) if(!ban[work[dep][i].id]&&vis[i]){
fat[work[dep][i].x]=work[dep][i].x; fat[work[dep][i].y]=work[dep][i].y;
}
s=tmp; lor(i,1,s) work[dep][i]=up[i];
lor(i,l,r) ban[qid[i]]=false;
return ans;
}
inline void radish(int dep,int l,int r,int &s){
lor(i,l,r) ban[qid[i]]=true;
int tmp=0; lor(i,1,s) vis[i]=false;
sort(work[dep]+1,work[dep]+1+s,cmpb);
lor(i,1,s){
if(unionn(work[dep][i].x,work[dep][i].y)) vis[i]=true;
}
lor(i,1,s){
fat[work[dep][i].x]=work[dep][i].x; fat[work[dep][i].y]=work[dep][i].y;
}
lor(i,1,s){
if(ban[work[dep][i].id]||vis[i]){
up[++tmp]=work[dep][i];
}
}
s=tmp; lor(i,1,s) work[dep][i]=up[i];
lor(i,l,r) ban[qid[i]]=false;
}