开发笔记:.NET6优先队列PriorityQueue

在最近发布的 .NET 6 中，包含了一个新的数据结构，优先队列 PriorityQueue， 实际上这个数据结构在隔壁 Java中已经存在了很多年了, 那优先队列是怎么实现的呢

本文主要介绍了 .NET 6 新增的数据结构优先队列，感兴趣的也可以看一下 PriorityQueue 的源码, 其实就是基于堆这种结构实现的，也展示了入队和出队的堆结构的变化过程

另外需要注意的是，堆这种结构不是稳定的，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作

所以以相同优先级入队的元素并不能保证以相同的顺序出队。

时间复杂度

因为接下来会分析时间复杂度, 这里先贴一张几种时间复杂度的对比图，从低阶到高阶有：O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )。

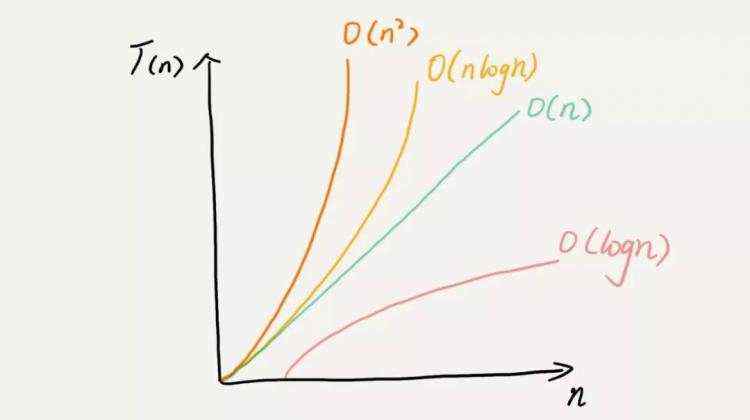
 什么是优先队列

首先，队列大家都知道, 是一个非常基础的数据结构, 它的特点是先进先出（FIFO）。

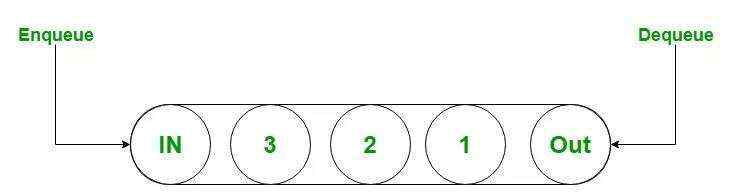
 而优先队列却不一定是先进先出，因为每个元素都有一个权重值, 代表着元素出队的优先级。

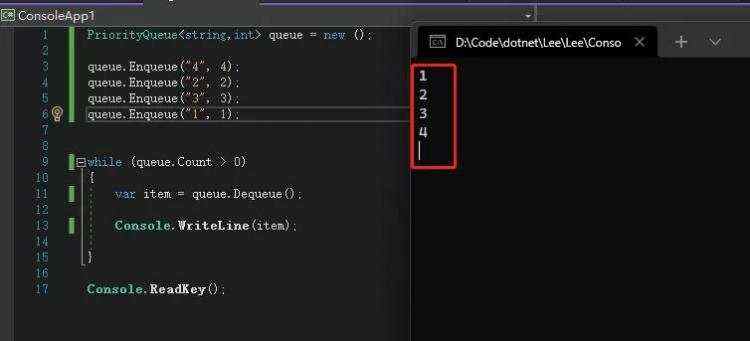
 队列可以用数组和链表实现, 简单、高效, 这样入队和出队的时间复杂度都是 O(1)。

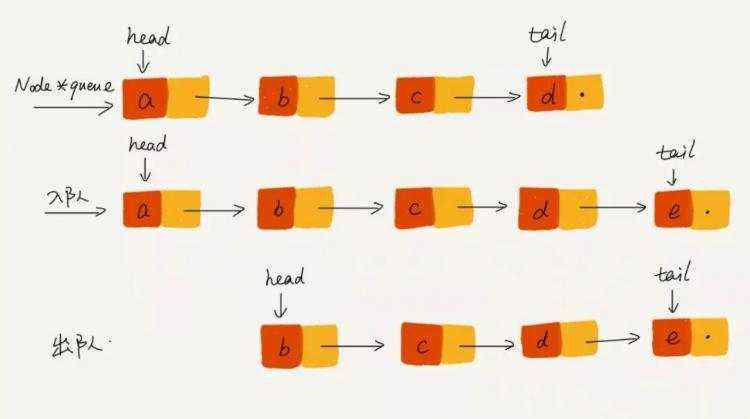
优先队列能不能使用上面的方法呢？也可以, 但是每次新元素入队后, 需要和队列内的元素进行遍历和大小对比, 然后插入到合适的位置, 让整个序列保持从大到小或者从小到大，这样入队的时间复杂度变成 O(n)， 而出队复杂度不变, 还是 O(1)。

O(n) 代表入队的时间是线性增长的, 效率较低, 有没有更高效的方法呢？

 
堆 Heap

堆这种数据结构的应用场景非常多，最经典的莫过于堆排序了, 堆排序是一种原地的、时间复杂度为 O(nlog n) 的排序算法，另外，堆也很适合用来做优先队列。

堆和树的结构其实是相似的, 堆有二叉堆, d-ary 堆, 2-3 堆, 斐波那契堆等等, 堆有一个特点就是每个父节点都大于等于它的儿子节点, 这种是大顶堆, 或者每个父节点都小于等于它的儿子节点, 这种是小顶堆，另外堆的儿子不分左右, 其中 java 中的 PriorityQueue 就是用二叉小顶堆实现的。

上面就是二叉堆, 而 .NET 6 中的 PriorityQueue 是由 d-ary 堆实现的, 而 d 表示父节点有几个儿子节点, .NET 6 中指定这个值为4，并且是小顶堆，也就是 “四叉小顶堆"。

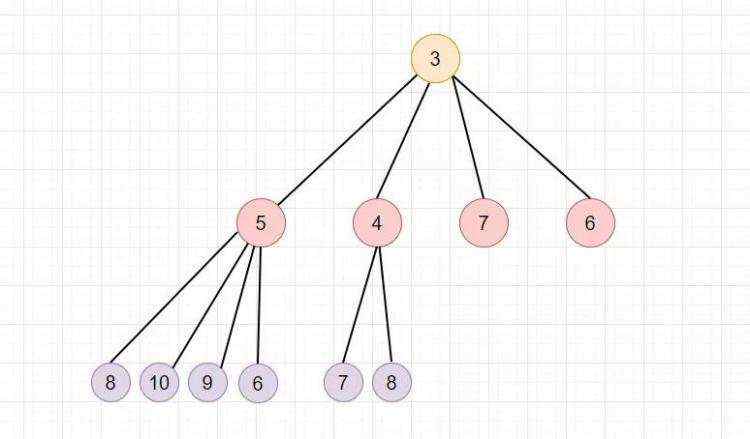
 那么如何在代码中实现呢？其实可以用数组存储堆, 我们可以通过”广度优先遍历“ 的方法, 把堆的节点映射到一个数组中，如下

另外，堆和数组之间还有下面的关系

1.堆的顶点就是数组的第一个元素，也是最小的元素。
2.通过子节点的下标，就可以通过公式计算出父节点的下标, 公式为
P = (C - 1) / 4
其中 P = 父节点的下标, C = 子节点的下标

 现在优先队列的数据结构确定了, 接下来看元素的入队和出队。

入队 Enqueue

使用堆来实现优先队列，入队操作2步完成, 非常简单！

1.添加新节点到末尾
2.通过上面的公式 P = (C - 1) / 4, 新的子节点和父节点进行大小对比，如果子节点比较小，那么就和父节点交换，重复这个过程，直到子节点大于或等于父节点，或者子节点变成堆顶，堆化完成, 这个交换过程是从下往上的, 入队的时间复杂度是 O(log n)。

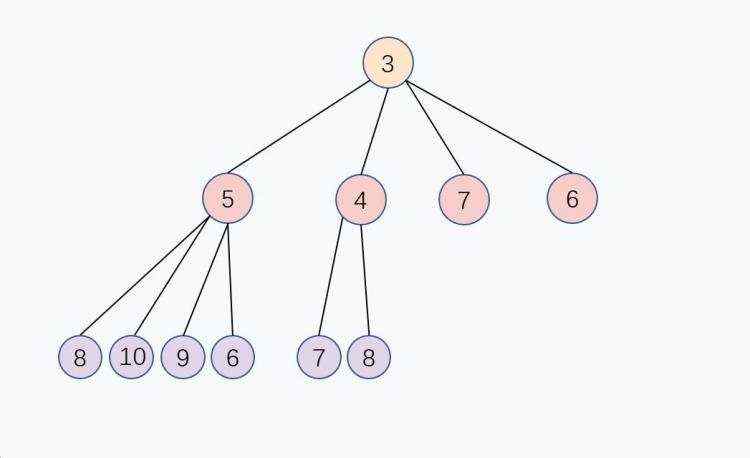
 出队 Dequeue

出队，就是每次取队列内最小的元素，基小顶堆结构，其实只需要取堆顶的元素即可，对应数组的第1个元素 array[0]。

你会发现，当取出堆顶元素以后，小顶堆的顶已经空了, 为了保持堆的结构，我们需要重新堆化。

和上面的入队 Enqueue 的逻辑有异曲同工之妙, 我们可以取堆的最后一个元素，把它放到堆顶, 然后父节点去和4个儿子节点比大小，如果比儿子节点大，就交换， 重复这个过程，直到父节点比4个儿子节点都大,

或者到达堆的最后一层，堆化完成，这个交换过程是从上往下的,出队的时间复杂度同样是 O(log n)。

另外，如果多个儿子节点都比父节点小，那父节点和最小的子节点交换。

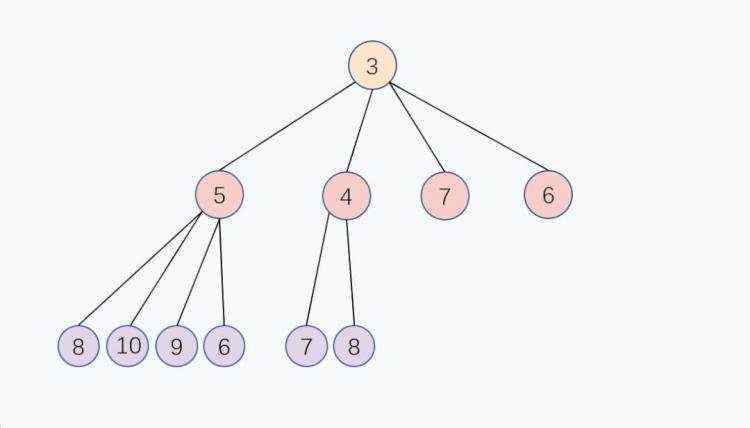
 扩容和收缩机制

优先队列是用数组实现的四叉小顶堆, 那么就存在数组的扩容和收缩的情况

扩容：最小为4，数组满的时候会扩大为当前容量的2倍。

收缩：数组不会自动收缩，不过可以手动调用 TrimExcess() 方法, 当空余的空间大于10% 的时候, 数组的长度会收缩到当前队列元素的数量。