卡尔曼_卡尔曼滤波（2）线性卡尔曼滤波

先来对比一下卡尔曼滤波和递归最小二乘法的整个算法过程&＃xff1a;

卡尔曼滤波算法

形式非常接近。可见相比递推最小二乘法&＃xff0c;卡尔曼就是相当于在两次迭代之间多了一步系统的状态转移&＃xff0c;也就是

这一项。 其实&＃xff0c;卡尔曼滤波就是递推最小二乘法的一种特殊情况&＃xff0c;卡尔曼滤波也是去通过最小化方差来求得最优的估计值。

卡尔曼滤波的更新过程为

第1步&＃xff0c;首先&＃xff0c;

已知&＃xff0c;然后由

算出

&＃xff0c;再由

算出

&＃xff0c;有了这些参数后&＃xff0c;结合观测值

就能估计出

&＃xff0c;再利用

更新

&＃xff1b;第2步.....

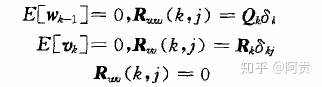
过程噪声和观测噪声是均值为零的高斯白噪声过程&＃xff0c;而且ω和υ是互不相关的。其中

是系统干扰方差矩阵&＃xff0c;是对称非负定矩阵&＃xff0c;

是观测噪声方差矩阵&＃xff0c;δ是狄拉克函数&＃xff0c;即

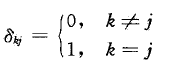
卡尔曼滤波器与我们前面讨论过的线性递归最小二乘滤波器非常相似。 但是递归最小二乘更新静态参数的估计&＃xff0c;而卡尔曼滤波器能够更新和估计不断变化的状态。 卡尔曼滤波器的目标是对该状态进行概率估计并使用两个步骤实时更新它&＃xff1a;预测和纠正。

为了使这些想法更具体&＃xff0c;让我们考虑一个估计车辆一维位置的问题。从时间k减1时的初始概率估计开始&＃xff0c;我们的目标是使用一个运动模型&＃xff0c;该模型可以从车轮里程计或惯性传感器测量中得出&＃xff0c;以预测我们的新状态。然后&＃xff0c;我们将使用GPS导出的观测模型来修正时间k时的车辆位置预测。每个分量、初始估计、预测状态和最终校正状态都是随机变量&＃xff0c;我们将通过它们的平均值和协方差来指定。这样&＃xff0c;我们可以将卡尔曼滤波器视为一种融合来自不同传感器的信息的技术&＃xff0c;以产生某种未知状态的最终估计&＃xff0c;同时考虑到运动和测量中的不确定性。

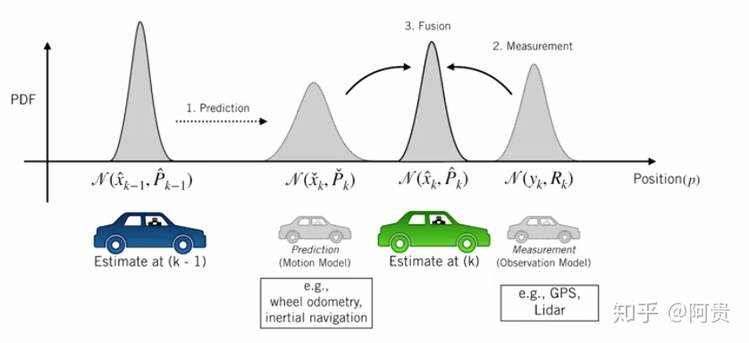
对于卡尔曼滤波算法&＃xff0c;我们可以用以下方法编写运动模型&＃xff1a;

时间步k的估计是时间步k减去1的估计&＃xff0c;控制输入和一些零平均噪声的线性组合。输入是影响系统状态演变的外部信号。例如&＃xff0c;在自动驾驶车辆的情况下&＃xff0c;这可能是用于加速和变换车道的车轮扭矩。

接下来&＃xff0c;我们还需要定义一个线性测量模型。最后&＃xff0c;我们需要一个和以前一样的测量噪声和一个过程噪声&＃xff0c;它代表着我们对线性动力系统是正确的确信度&＃xff0c;换句话说&＃xff0c;我们对控制输入的影响有多不确定。

一旦我们建立了系统&＃xff0c;我们就可以使用一种与递归最小二乘视频中讨论的方法非常相似的方法。但有一点不同&＃xff0c;这次我们将分两步完成。

首先&＃xff0c;我们使用过程模型来预测我们的状态&＃xff0c;记住&＃xff0c;我们现在通常谈论自上一个时间步骤以来演变的演化状态和非状态参数&＃xff0c;并将传播我们的不确定性。

第二&＃xff0c;我们将使用我们的测量&＃xff0c;根据我们的测量残差以及我们的最佳收益来修正预测。最后&＃xff0c;我们将使用增益将状态协方差从我们的预测传播到我们的修正估计。

在我们的记数法中&＃xff0c;

表示在特定时间步的一个修正的预测&＃xff0c;而

表明在合并测量之前有一个预测。如果你以前使用过卡尔曼滤波器&＃xff0c;你可能也看到过它分别用

来表示修正的以及

来表示预测的量。

让我们回顾一下。我们从状态的概率密度开始&＃xff0c;时间步k减去1的参数&＃xff0c;我们将其表示为多元高斯。然后&＃xff0c;我们使用线性预测模型预测时间步骤k的状态&＃xff0c;并随着时间传播平均值和不确定性&＃xff08;协方差&＃xff09;。最后&＃xff0c;利用我们的概率测量模型&＃xff0c;我们通过我们的最佳增益矩阵k将我们测量的信息与先前的预测进行最佳融合&＃xff0c;从而纠正我们的初始预测。我们的最终结果是我们在时间步骤k时状态的更新概率估计。

下面以一个小例子来应用一下卡尔曼滤波

再次考虑自动驾驶车辆估计其自身位置的情况。 我们的状态向量将包括车辆位置及其一阶导数。 我们的输入将是一个标量加速度&＃xff0c;可能来自控制系统&＃xff0c;命令我们的汽车向前或向后加速。 对于我们的测量&＃xff0c;我们假设我们能够直接使用类似GPS接收器的方式确定车辆位置。 最后&＃xff0c;我们将如下定义噪声方差。&＃xff08;公式有误&＃xff0c;应该为

&＃xff09;

给定这个初始估计和我们的数据&＃xff0c;在我们使用卡尔曼滤波器执行一个预测步骤和一个校正步骤之后&＃xff0c;我们的校正位置估计是多少&＃xff1f;

这是我们如何使用这些定义来解决我们的校正位置和速度估计。

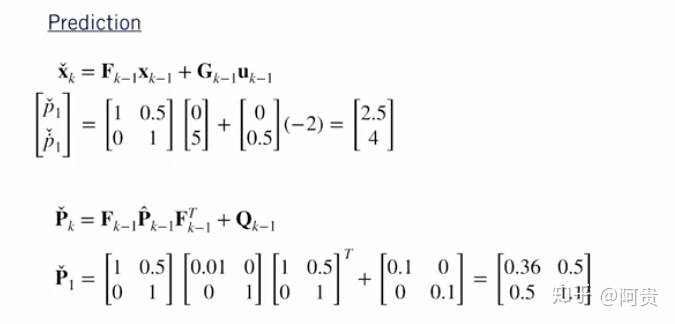
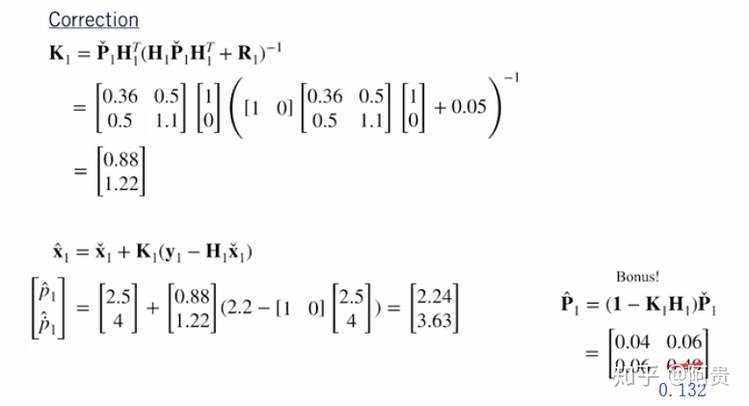
注意我们的最终校正状态协方差较小的事实。 这就是我们在结合位置测量后对汽车的位置更加确定。 这种不确定性的降低是因为我们的测量模型相当准确。 也就是说&＃xff0c;测量噪声方差非常小。 尝试增加测量方差并观察最终状态估计会发生什么。

总而言之&＃xff0c;卡尔曼滤波器类似于递归平方&＃xff0c;但也增加了一个运动模型&＃xff0c;定义了我们的状态随时间的演变。 卡尔曼滤波器分两个阶段工作&＃xff1a;第一&＃xff0c;使用运动模型预测下一状态&＃xff0c;第二&＃xff0c;使用测量校正该预测。

这有一篇翻译了国外的博客文章写得很好&＃xff0c;可以看一下。

卡尔曼滤波器推导与解析 - 案例与图片 - 李小铭 - 博客园

参考&＃xff1a;

https://blog.csdn.net/ethan_guo/article/details/80568254