KNN算法在海伦约会预测中的应用

准备工作

在上一篇文章的基础上，我们将详细探讨如何完成从数据导入到算法预测的全过程。本次实验所需的数据集是海伦约会数据集，数据存储在一个文本文件中。考虑到GitHub访问速度的问题，已将数据集上传至百度网盘供读者下载。

下载链接请点击此处，提取码为：wspl。

准备工作完成后，我们将开始实现KNN算法（不了解KNN算法原理的读者可查阅本系列相关文章）。

数据导入

打开文本文件后，可以看到文件包含四列数据，其中前三列为特征值，最后一列为标签，各列之间以制表符分隔。

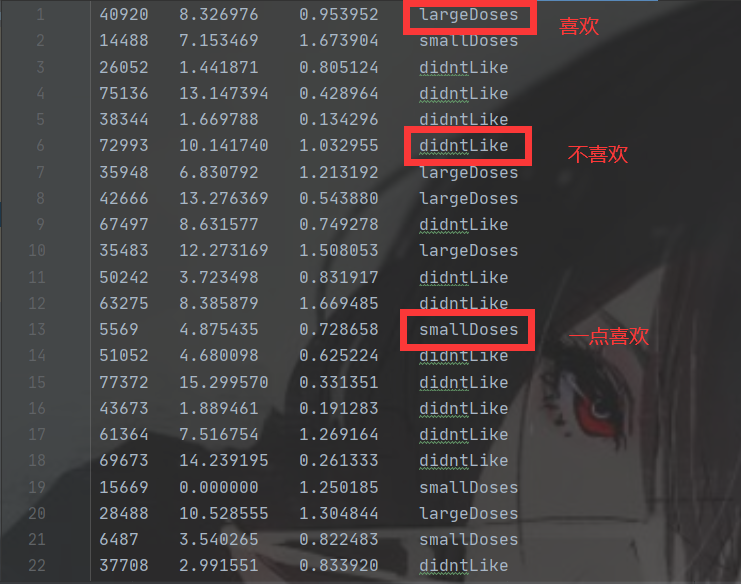
接下来，我们将通过Python脚本读取文件的每一行，并使用split()方法提取特征数据，同时构建相应的标签列表。最终返回一个特征矩阵和标签列表。具体代码如下：

import numpy as np
import operator
from matplotlib.font_manager import FontProperties

# 读取数据集
def file2matrix(filename):
    with open(filename, 'r') as fr:
        lines = fr.readlines()
        numberOfLines = len(lines)
        returnMat = np.zeros((numberOfLines, 3))
        classLabelVector = []
        index = 0
        for line in lines:
            line = line.strip()
            listFromLine = line.split('\t')
            returnMat[index, :] = listFromLine[0:3]
            if listFromLine[-1] == 'didntLike':
                classLabelVector.append(1)
            elif listFromLine[-1] == 'smallDoses':
                classLabelVector.append(2)
            elif listFromLine[-1] == 'largeDoses':
                classLabelVector.append(3)
            index += 1
    return returnMat, classLabelVector

数据分析

在KNN算法中，新数据点的分类基于其与已有数据点之间的距离。然而，当某一特征值显著大于其他特征时，可能会导致其他特征的影响被忽略。因此，我们需要对数据进行归一化处理，确保所有特征在同一尺度上，以避免某些特征因数值较大而主导分类结果。

数据归一化的公式为：

通过这一公式，我们可以将每个特征的数据缩放到0到1之间。以下是数据归一化的具体实现：

def autoNorm(dataSet):
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = np.zeros(np.shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - np.tile(minVals, (m, 1))
    normDataSet = normDataSet / np.tile(ranges, (m, 1))
    return normDataSet, ranges, minVals

数据可视化

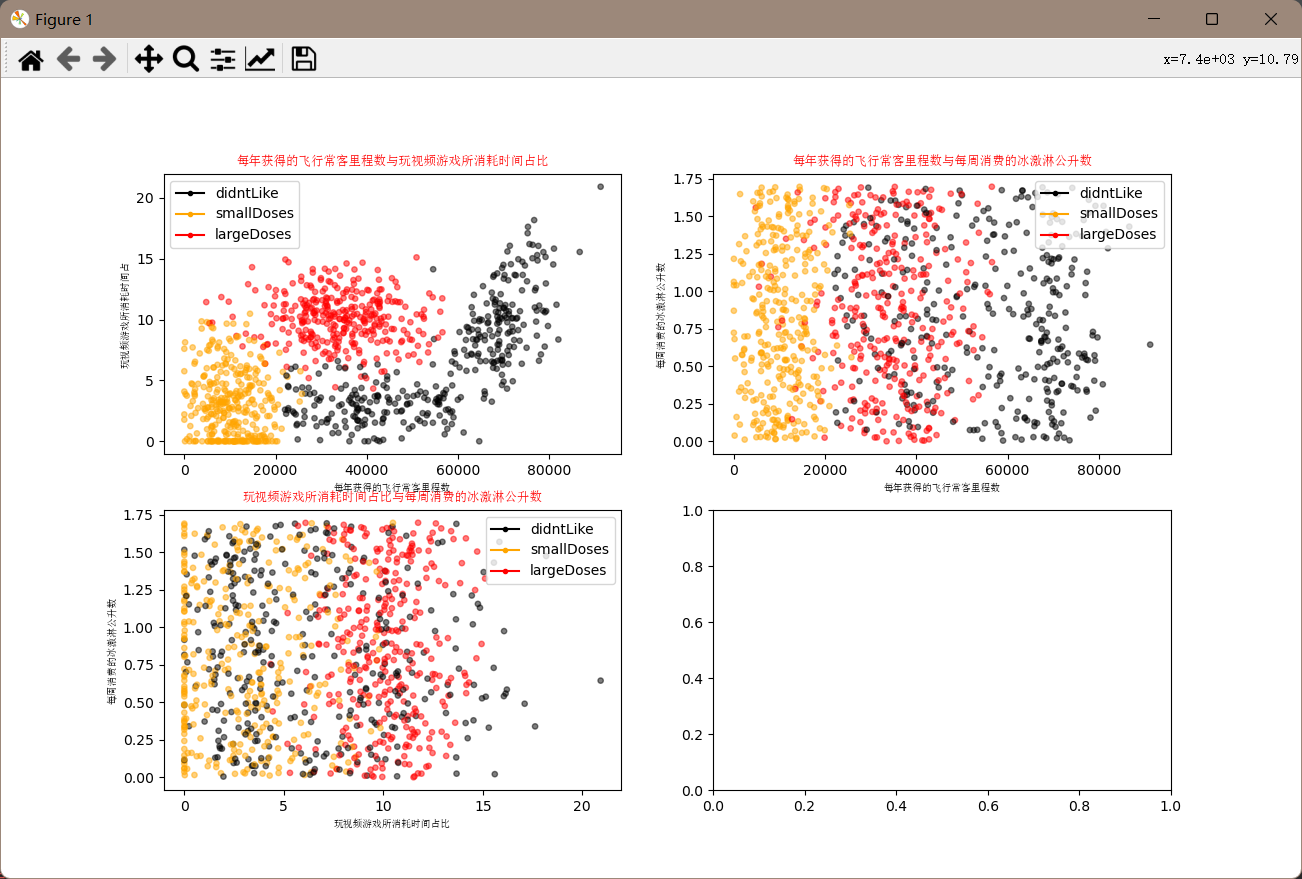
为了更好地理解数据，我们将使用matplotlib库对数据进行可视化。以下是数据可视化的具体代码实现：

def showdatas(datingDataMat, datingLabels):
    fOnt= FontProperties(fname=r'c:\windows\fonts\simsun.ttc', size=14)
    fig, axs = plt.subplots(nrows=2, ncols=2, sharex=False, sharey=False, figsize=(13, 8))
    LabelsColors = []
    for i in datingLabels:
        if i == 1:
            LabelsColors.append('black')
        if i == 2:
            LabelsColors.append('orange')
        if i == 3:
            LabelsColors.append('red')
    
    axs[0][0].scatter(x=datingDataMat[:, 0], y=datingDataMat[:, 1], color=LabelsColors, s=15, alpha=.5)
    axs0_title_text = axs[0][0].set_title('飞行常客里程数与玩视频游戏时间占比', FOntProperties=font)
    axs0_xlabel_text = axs[0][0].set_xlabel('飞行常客里程数', FOntProperties=font)
    axs0_ylabel_text = axs[0][0].set_ylabel('玩视频游戏时间占比', FOntProperties=font)
    plt.setp(axs0_title_text, size=9, weight='bold', color='red')
    plt.setp(axs0_xlabel_text, size=7, weight='bold', color='black')
    plt.setp(axs0_ylabel_text, size=7, weight='bold', color='black')
    
    axs[0][1].scatter(x=datingDataMat[:, 0], y=datingDataMat[:, 2], color=LabelsColors, s=15, alpha=.5)
    axs1_title_text = axs[0][1].set_title('飞行常客里程数与每周消费冰激凌量', FOntProperties=font)
    axs1_xlabel_text = axs[0][1].set_xlabel('飞行常客里程数', FOntProperties=font)
    axs1_ylabel_text = axs[0][1].set_ylabel('每周消费冰激凌量', FOntProperties=font)
    plt.setp(axs1_title_text, size=9, weight='bold', color='red')
    plt.setp(axs1_xlabel_text, size=7, weight='bold', color='black')
    plt.setp(axs1_ylabel_text, size=7, weight='bold', color='black')
    
    axs[1][0].scatter(x=datingDataMat[:, 1], y=datingDataMat[:, 2], color=LabelsColors, s=15, alpha=.5)
    axs2_title_text = axs[1][0].set_title('玩视频游戏时间占比与每周消费冰激凌量', FOntProperties=font)
    axs2_xlabel_text = axs[1][0].set_xlabel('玩视频游戏时间占比', FOntProperties=font)
    axs2_ylabel_text = axs[1][0].set_ylabel('每周消费冰激凌量', FOntProperties=font)
    plt.setp(axs2_title_text, size=9, weight='bold', color='red')
    plt.setp(axs2_xlabel_text, size=7, weight='bold', color='black')
    plt.setp(axs2_ylabel_text, size=7, weight='bold', color='black')
    
    didntLike = mlines.Line2D([], [], color='black', marker='.', markersize=6, label='不喜欢')
    smallDoses = mlines.Line2D([], [], color='orange', marker='.', markersize=6, label='有些喜欢')
    largeDoses = mlines.Line2D([], [], color='red', marker='.', markersize=6, label='非常喜欢')
    
    axs[0][0].legend(handles=[didntLike, smallDoses, largeDoses])
    axs[0][1].legend(handles=[didntLike, smallDoses, largeDoses])
    axs[1][0].legend(handles=[didntLike, smallDoses, largeDoses])
    
    plt.show()

通过上述代码，我们生成了三个散点图，分别展示了不同特征之间的关系，并用不同颜色标记了不同的分类结果。

算法预测

KNN算法的核心部分保持不变，主要变化在于数据的输入。以下是KNN算法的具体实现：

def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]
    diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances**0.5
    sortedDistIndicies = distances.argsort()
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

程序运行结果

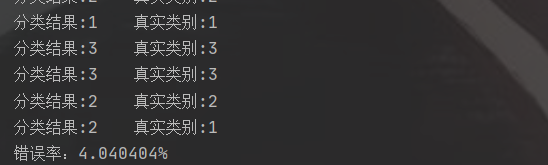
运行上述算法，可以得到如下结果：

具体实现代码如下：

if __name__ == '__main__':
    resultList = ['不喜欢', '有些喜欢', '非常喜欢']
    datingDataMat, datingLabels = file2matrix('dataset.txt')
    normMat, ranges, minVals = autoNorm(datingDataMat)
    hoRatio = 0.10
    m = normMat.shape[0]
    numTestVecs = int(m * hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 4)
        print(f'分类结果: {classifierResult}, 真实类别: {datingLabels[i]}')
        if classifierResult != datingLabels[i]:
            errorCount += 1.0
    print(f'错误率: {errorCount / float(numTestVecs) * 100}%')
    showdatas(datingDataMat, datingLabels)

总结

海伦约会预测的实现过程与基本的KNN算法类似，主要区别在于数据的处理和导入方式。我们对数据进行了归一化处理，并通过可视化手段直观地展示了数据特征。通过测试集计算了算法的错误率，验证了模型的有效性。