
期来介绍一下Xbar-R(均值-极差)控制图,希望下面分享的能给朋友们理解和应用统计过程控制带来启发和帮助,统计技术本身不会解决质量过程的各种问题,无论如何还是得实际的过程应用中适时结合相应的产品才能发挥效能,以至于把控制图识别出来的问题解决。我们来一起学习统计科学在质量中的应用,小编特意把它分割成若干个小节,推送到本号中,通过碎片化得时间,一点一滴的积累,逐步学会它并应用到实际质量控制之中。
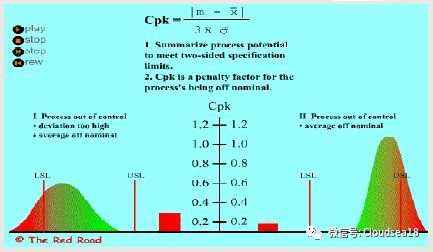
对于计量值数据, Xbar-R(均值一极差)控制图是最常用,最重要的控制图,因为它具有下列优点:
1. 适用范围广。对于Xbar图而言,计量值数据X服从正态分布是经常出现的。若X非正态分布,则当样本大小n≤4或5时,根据中心极限定理,知道Xbar近似正态分布。对于R图而言, 通过在电子计算机上的统计模拟实验证实,只要总体分布不是太不对称的,R的分布没有大的变化。这就从理论上说明了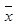 一R图适用的范围广泛。
一R图适用的范围广泛。
2.灵敏度高。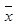 图的统计量为均值
图的统计量为均值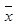 ,反映在x上的偶然波动是随机的,通过均值的平均作用,这种偶然波动得到一定程度的抵消;而反映在x上的异常波动往往是在同一个方向的,它不会通过均值的平均作用抵消。因此,正图检出异常的能力高。至于R图的灵敏度则不如图Xbar高。
,反映在x上的偶然波动是随机的,通过均值的平均作用,这种偶然波动得到一定程度的抵消;而反映在x上的异常波动往往是在同一个方向的,它不会通过均值的平均作用抵消。因此,正图检出异常的能力高。至于R图的灵敏度则不如图Xbar高。
现在说明一下一R图的统计基础,假定质量特性服从正态分布N(μ,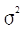 ),且μ,σ均已知。若x1,x2,...,xn是大小为n的样本,则样本均值为
),且μ,σ均已知。若x1,x2,...,xn是大小为n的样本,则样本均值为
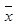 =
=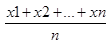
由于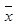 服从正态分布N(μ,
服从正态分布N(μ,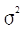 /n),并且样本均值落入下列两个界限
/n),并且样本均值落入下列两个界限
μ-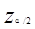
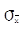 =μ-
=μ-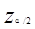
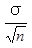 (1a)
(1a)
μ+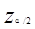
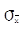 =μ+
=μ+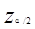
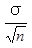 (1b)
(1b)
间的概率为1-α。因此若μ与σ已知,则式(1a)与式(1b)可分别作为样本均值的控制图的上下控制界限。如前述,通常取Za/2=3,即采用3σ控制界限。当然,即使x的分布是非正态的,但由于中心极限定理,上述结果也近似成立。
在实际工作中,μ与σ通常未知,这时就必须应用从稳态过程所取的预备样本的数据对它们进行估计。预备样本通常至少取25个(根据判稳准则(2),最好至少取35个预备样本)。设取 m个样本,每个样本包含n个观测值。样本大小n主要取决于合理分组的结构,抽样与检查的费用,参数估计的效率等因素,n通常取为4,5或6。令所取的m个样本的均值分别为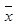 1,
1,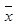 2,...,
2,..., 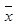 m,则过程的μ的最佳估计量
m,则过程的μ的最佳估计量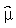 为总均值,即
为总均值,即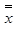
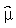 =
=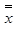 =(
=(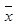 1+
1+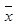 2+…+
2+…+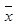 m)/m
m)/m
于是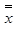 可作为
可作为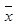 图的中心线。
图的中心线。
为了建立控制界限,需要估计过程的标准差σ可以根据m个样本的极差或标准差来进行估计。应用极差进行估计的优点是极差计算简单,所以至今R图的应用较s图为广。
现在讨论极差法。设x1,x2,...,xn为一大小为n的样本,则此样本的极差R为最大观测值xmax与最小观测值xmin之差,即
R= xmax-xmin
若样本取自正态总体,可以证明样本极差R与总体标准差σ有下列关系:令W=R/σ,可以证明 E(W)=d2,为一与样本大小n有关的常数,于是,σ的估计量为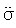 =E(R)/d2。
=E(R)/d2。
令m个样本的极差为R1,R2,...,Rm,则样本平均极差为
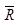 =
=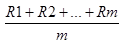
故σ的估计量为
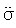 =E(R)/d2
=E(R)/d2
若样本大小n较小,则用极差法估计总体方差与用样本方差去估计总体方差的效果是一样的。但当n较大,如n>10或12,则由于极差没有考虑样本在xmax与xmin之间的观测值的信息, 故极差法的效率迅速降低。但在实际工作中, 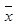 一R图一般取n=4,5或6,所以极差法是令人满意的。
一R图一般取n=4,5或6,所以极差法是令人满意的。
若取μ的估计量为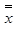 ,σ的估计量为E(R)/d2,则
,σ的估计量为E(R)/d2,则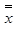 图的控制线为
图的控制线为
UCL=μ+ 3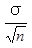 ≈
≈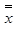 + 3
+ 3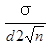
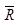 =
=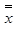 +
+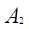
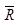
CL=μ≈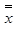
LCL=μ-3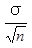 ≈
≈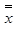 -3
-3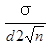
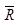 =
=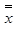 -
-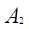
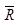
式中
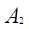 =3
=3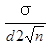
为一与样本大小n有关的常数,参见计量值控制图系数表。
由上述,已知样本极差R与过程标准差σ有关,因此可以通过R来控制过程的变异度,这就是R图。R图的中心线即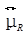 =
=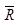 。为了确定R图的控制界限,需要对σR进行估计。若质量特性服从正态分布,令W=R/σ,可以证明σw=d3(d3为一与样本大小n有关的常数),于是从R =Wσ知知σR =σwσ=d3σ。由于σ未知,故从式
。为了确定R图的控制界限,需要对σR进行估计。若质量特性服从正态分布,令W=R/σ,可以证明σw=d3(d3为一与样本大小n有关的常数),于是从R =Wσ知知σR =σwσ=d3σ。由于σ未知,故从式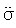 =E(R)/d2得σR的估计量为
=E(R)/d2得σR的估计量为
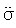 =d3
=d3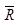 /d2
/d2
根据上述,得到R图的控制线如下

令D3=1-3d3/d2,D4=1+3d3/d2,则代入上式后,得R图的控制线为
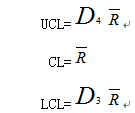
式中,系数D3、D4参见计量值控制图系数表。
下一辑我们通过例子来说明建立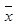 一R图的步骤,其他控制图的建立步骤也与此类似。
一R图的步骤,其他控制图的建立步骤也与此类似。
推荐阅读:
统计过程控制-Statistical Process Control(SPC),实战篇;统计过程控制-Statistical Process Control(SPC),实战篇;质量管理IATF16949五大核心工具之SPC;纯干货-统计过程控制(SPC)与休哈特控制图(1);统计过程控制(SPC)和休哈特控制图(2);统计过程控制(SPC)和休哈特控制图(3);休哈特控制图之四,分析用控制图与控制用控制图;休哈特控制图的设计思想;统计过程控制(SPC)和休哈特控制图之七,休哈特控制图的种类及其用途;品质数据统计过程控制,基础分析
统计过程控制(SPC)和休哈特控制图之八 应用控制图需要考虑的8个问题
新手也能秒懂的SPC、Cpk、Ppk应用简介
品质人生
∣一个致力于专业有态度的公众号
