解释梯度反方向是函数值下降最快的方向

首先&＃xff0c;先引用知乎大佬的一句话&＃xff1a;平面(一维)导数为正&＃xff0c;单调增加&＃xff0c;导数为负单调减。可以这里的正负号理解成一维向量的方向。

转自知乎专栏机器学习算法与自然语言处理     忆臻大佬文章&＃xff1a;

刚接触梯度下降这个概念的时候&＃xff0c;是在学习机器学习算法的时候&＃xff0c;很多训练算法用的就是梯度下降&＃xff0c;然后资料和老师们也说朝着梯度的反方向变动&＃xff0c;函数值下降最快&＃xff0c;但是究其原因的时候&＃xff0c;很多人都表达不清楚。所以我整理出自己的理解&＃xff0c;从方向导数这个角度把这个结论证明出来&＃xff0c;让我们知其然也知其所以然~

下面我一开始不提梯度的概念&＃xff0c;完全根据自己的理解进行下文的梳理&＃xff0c;一步一步推出梯度的来历&＃xff1a;

• 导数

导数的几何意义可能很多人都比较熟悉: 当函数定义域和取值都在实数域中的时候&＃xff0c;导数可以表示函数曲线上的切线斜率。 除了切线的斜率&＃xff0c;导数还表示函数在该点的变化率。

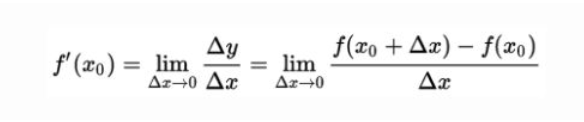
将上面的公式转化为下面图像为

直白的来说&＃xff0c;导数代表了在自变量变化趋于无穷小的时候&＃xff0c;函数值的变化与自变量变化的比值代表了导数&＃xff0c;几何意义有该点的切线。物理意义有该时刻的&＃xff08;瞬时&＃xff09;变化率...

注意在一元函数中&＃xff0c;只有一个自变量变动&＃xff0c;也就是说只存在一个方向的变化率&＃xff0c;这也就是为什么一元函数没有偏导数的原因。

• 偏导数

既然谈到偏导数&＃xff0c;那就至少涉及到两个自变量&＃xff0c;以两个自变量为例&＃xff0c;z&＃61;f(x,y) . 从导数到偏导数&＃xff0c;也就是从曲线来到了曲面. 曲线上的一点&＃xff0c;其切线只有一条。但是曲面的一点&＃xff0c;切线有无数条。

而我们所说的偏导数就是指的是多元函数沿坐标轴的变化率.

那么偏导数对应的几何意义是是什么呢&＃xff1f;

• 偏导数

  假设山坡表示为

  那么我们来考虑如何求出方向的斜率&＃xff0c;可以类比于前面导数定义&＃xff0c;得出如下&＃xff1a;

  设为一个二元函数&＃xff0c;为一个单位向量&＃xff0c;如果下列的极限值存在

  此方向导数记为

  则称这个极限值是沿着方向的方向导数&＃xff0c;那么随着的不同&＃xff0c;我们可以求出任意方向的方向导数.这也表明了方向导数的用处&＃xff0c;是为了给我们考虑函数对任意方向的变化率.

  在求方向导数的时候&＃xff0c;除了用上面的定义法求之外&＃xff0c;我们还可以用偏微分来简化我们的计算.

  表达式是&＃xff1a;&＃xff08;至于为什么成立&＃xff0c;很多资料有&＃xff0c;不是这里讨论的重点&＃xff09;

  那么一个平面上无数个方向&＃xff0c;函数沿哪个方向变化率最大呢&＃xff1f;

  目前我不管梯度的事&＃xff0c;我先把表达式写出来&＃xff1a;

  

  设,

  那么我们可以得到&＃xff1a;

  (为向量与向量之间的夹角)

  那么此时如果要取得最大值&＃xff0c;也就是当为0度的时候&＃xff0c;也就是向量&＃xff08;这个方向是一直在变&＃xff0c;在寻找一个函数变化最快的方向&＃xff09;与向量&＃xff08;这个方向当点固定下来的时候&＃xff0c;它就是固定的&＃xff09;平行的时候&＃xff0c;方向导数最大.方向导数最大&＃xff0c;也就是单位步伐&＃xff0c;函数值朝这个反向变化最快.

  好了&＃xff0c;现在我们已经找到函数值下降最快的方向了&＃xff0c;这个方向就是和向量相同的方向.那么此时我把A向量命名为梯度&＃xff08;当一个点确定后&＃xff0c;梯度方向是确定的&＃xff09;&＃xff0c;也就是说明了为什么梯度方向是函数变化率最大的方向了&＃xff01;&＃xff01;&＃xff01;&＃xff08;因为本来就是把这个函数变化最大的方向命名为梯度&＃xff09;