【机器学习】SVM和核函数

上了吴恩达教授在Coursera上的课程之后，在网上找到了他在斯坦福课程的资料CS229 。下面会结合这两个课程的资料，整理一篇笔记。

背景

从之前的逻辑回归的模型中，我们可以看到，如果一个样本越远离决策边界(Decision Boundary)，那么我们就越能确保这个样本被正确分类。所以一个比较好的决策边界是尽量能让所有样本到决策边界的距离最大。从下图中可以看到，如果margin越大，我们对样本的正确分类就越有信心。

SVM就是一种能帮你得到margin最大的决策边界的算法。

SVM数学推导

在接下来的推导中，定义$y^{(i)}\in \{-1,1\}$y(i)∈{−1,1}，而不是$y\in\{0,1\}$y∈{0,1}。首先定义函数间隔(functional margin) 为:
$\hat{\gamma}^{(i)}=y^{(i)}(w^{T}x^{(i)}+b)$γ^​(i)=y(i)(wTx(i)+b)

如果$y^{(i)}=1$y(i)=1，那么我们希望$w^{T}x^{(i)}+b$wTx(i)+b能是一个很大的正数，相反，如果$y^{(i)}=-1$y(i)=−1，那么$w^{T}x^{(i)}+b$wTx(i)+b需要是一个很小的负数，这样就能使得样本离决策边界越远，分类效果越好。因此，得到的functional margin $\hat{\gamma}$γ^​越大，分类效果越好。
对于一个样本集$S=\{(x^{(i)},y^{(i)});i=1,...n\}$S={(x(i),y(i));i=1,...n}，定义：
$\hat{\gamma}=\min_{i=1,...n}\hat{\gamma}^{(i)}$γ^​=i=1,...nmin​γ^​(i)

那么接下来讨论 几何间隔(geometric margin) 。

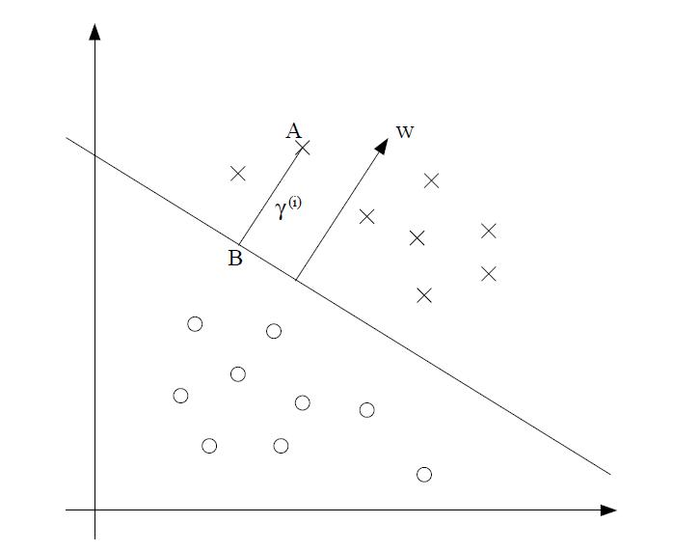
从上图中可以看到，向量$w$w一定是与超平面垂直的，我们取超平面上的任意两点$x_1,x_2$x1​,x2​，$x_1,x_2$x1​,x2​满足$wx_1+b=0$wx1​+b=0和$wx_2+b=0$wx2​+b=0，两式相减得到$w(x_1-x_2)=0$w(x1​−x2​)=0。因为向量$x_1-x_2$x1​−x2​肯定在超平面上，所以可以得到向量$w$w与这个超平面正交。
假设A为样本点，如何求A到超平面的几何间距$\gamma^{(i)}$γ(i)呢？假设点B是A到超平面的投影，那么向量B可以表示为$x^{(i)}-\gamma^{(i)}*\frac{w}{||w||}$x(i)−γ(i)∗∣∣w∣∣w​。而且由于B点位于决策边界上，所以：
$w^T(x^{(i)}-\gamma^{(i)}*\frac{w}{||w||})+b=0$wT(x(i)−γ(i)∗∣∣w∣∣w​)+b=0

得到$\gamma^{(i)}$γ(i)为：
$\gamma^{(i)}=(\frac{w}{||w||})^Tx^{(i)}+\frac{b}{||w||}$γ(i)=(∣∣w∣∣w​)Tx(i)+∣∣w∣∣b​

由于我们的样本是有正负之分的，综合正负样本可以得到：
$\gamma^{(i)}=y^{(i)}((\frac{w}{||w||})^Tx^{(i)}+\frac{b}{||w||})$γ(i)=y(i)((∣∣w∣∣w​)Tx(i)+∣∣w∣∣b​)

同时定义$\gamma=\min\limits_{i=1,...n}\gamma^{(i)}$γ=i=1,...nmin​γ(i)
从geometric margin的表达式可以看到，$w$w和$b$b的缩放对$\gamma$γ的值没有影响，所以我们可以把要求的最优化问题写成:
$\max_{y,w,b}\gamma\\ s.t.\space \space y^{(i)}(w^{T}x^{(i)}+b)\ge\gamma, i=1,...,n\\ ||w||=1$y,w,bmax​γs.t.  y(i)(wTx(i)+b)≥γ,i=1,...,n∣∣w∣∣=1
但这个问题并不是一个直接可解的优化问题。我们首先用functional matrix来代替geometric matrix：
$\max_{y,w,b}\frac{\hat{\gamma}}{||w||}\\ s.t.\space \space y^{(i)}(w^{T}x^{(i)}+b)\ge\hat{\gamma}, i=1,...,n$y,w,bmax​∣∣w∣∣γ^​​s.t.  y(i)(wTx(i)+b)≥γ^​,i=1,...,n

为了剔除$\hat{\gamma}$γ^​的影响，我们可以对$w$w和$b$b进行缩放，使得$\hat{\gamma}$γ^​为1.前面讨论过，对$w$w和$b$b同时缩放，并不会影响geometric function的大小，也不会影响最终的结果。
因此，上述问题可以简化成:
$\min_{w,b}\space \frac{1}{2}||w||^2\\ s.t. \space \space y^{(i)}(w^{T}x^{(i)}+b)\ge1, i=1,...,n$w,bmin​ 21​∣∣w∣∣2s.t.  y(i)(wTx(i)+b)≥1,i=1,...,n

现在我们把这个问题转换成能用已知的优化问题求解的形式了。

正则化

核函数