机器学习+模式识别学习总结（五）——集成学习

一、定义

1、集成学习&＃xff1a;集成学习的核心思想就是构建并结合多个学习器提升性能。

将多个分类方法聚集在一起&＃xff0c;以提高分类准确性&＃xff0c;可以是不同或相同的算法&＃xff08;异质集成/同质集成&＃xff09;&＃xff0c;最后通过某种方法把学习结果集成起来。是一种机器学习范式&＃xff0c;使用多个学习器来解决同一个问题。

2、集成学习两大类&＃xff1a;

&＃xff08;1&＃xff09;个体学习器之间存在强依赖关系&＃xff0c;必须串行生成的序列化方法&＃xff0c;如&＃xff0c;Boosting&＃xff1b;

&＃xff08;2&＃xff09;个体学习器之间不存在强依赖关系&＃xff0c;可同时生成并行化方法&＃xff0c;如&＃xff0c;Bagging和随机森林。

二、Boosting

1、简述&＃xff1a;Boosting是一种可将弱学习器提升为强学习器的算法。(强学习算法&＃xff1a;准确率很高的学习算法&＃xff1b;弱学习算法&＃xff1a;准确率不高&＃xff0c;仅比随机猜测略好。)

2、算法机制&＃xff1a;从初始训练集训练一个基学习器——根据基学习器的表现对训练样本分布进行调整——基于调整后的分布训练下一个基学习器——直至学习器数目达到事先设定的阈值T——将这T个基学习器加权结合&＃xff0c;让分类效果差的基学习器具有较小的权值

【注】&＃xff1a;

①Boosting中所有的弱学习器可以是不同类的分类器。

②每一轮改变训练数据权重或概率分布的方式&＃xff1a;通过提高那些在前一轮被弱分类器分错样例的权值&＃xff0c;减小前一轮分对样本的权值&＃xff0c;这样误分的样本在后续会受到更多关注。

③通过加法模型将弱分类器进行线性组合。

3、理论来源&＃xff1a;基于PAC(Probably Approximately Correct)学习模型的一种提高。

PAC&＃xff1a;Probably Approximate Correct直译过来就是“可能近似正确”&＃xff0c;这里面用了两个描述”正确”的词&＃xff0c;可能和近似。 “近似”是在取值上&＃xff0c;只要和真实值的偏差小于一个足够小的值就认为”近似正确”&＃xff1b;“可能”是在概率上&＃xff0c;即只要“近似正确”的概率足够大就认为“可能近似正确”。 

https://blog.csdn.net/qq_34662278/article/details/83961427

4、代表算法&＃xff1a;AdaBoost&＃xff0c;“可调节提升方法” (Adaptive Boosting)

&＃xff08;1&＃xff09;算法核心思想&＃xff1a;

①迭代。每轮迭代在训练集上产生新分类器&＃xff0c;使用该分类器对所有样本分类&＃xff0c;以评估每个样本的重要性(用于后面赋权值)。

②样本权重更新。初始为等概率分布&＃xff0c;因此每个样本分布的初始权值为1/N&＃xff0c;每次循环后&＃xff0c;提高错误样本的分布概率&＃xff0c;使错分样本占比增大&＃xff0c;下一次循环弱学习器着重判断&＃xff0c;同时正确分类的样本权重降低&＃xff0c;其“抽中”的概率会减小。

③弱学习器的权重。准确率越高的弱学习器权值越高。当循环到一定次数或某度量标准符合要求时&＃xff0c;停止循环&＃xff0c;然后将弱学习器按其相应的权重加权组成强学习器。

&＃xff08;2&＃xff09;基本思路&＃xff1a;

①训练一系列弱学习器h1,h2,h3,...,hT。

②训练过程中注重那些分类错误的样本。

③把训练出来的一系列弱学习器组合起来&＃xff0c;每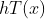个弱学习器都有一个相应的权重&＃xff0c;

。

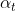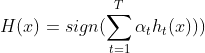&＃xff08;3&＃xff09;AdaBoost的权重更新计算&＃xff1a;

①基学习器权值&＃xff1a;

②训练样本权值&＃xff1a;

错误分类样本的权值更新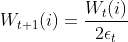&＃xff1a;

正确分类样本的权值更新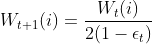&＃xff1a;

&＃xff08;4&＃xff09;AdaBoost总结&＃xff1a;

①核心思想是关注被错分的样本&＃xff0c;注重性能好的弱分类器。

②样本权重间接影响分类器权重。

③阈值的选取规则是选取使分类错误率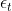最小的阈值。

④不改变训练数据&＃xff0c;而不断改变训练数据权值分布&＃xff0c;使训练数据在基本分类器中起不同作用。

⑤利用基本分类器的线性组合构建最终分类器。

 三、Bagging与随机森林

&＃xff08;一&＃xff09;Bagging(Bootstrap Aggregating)&＃xff1a;

Bagging是一种并行式集成学习方法&＃xff0c;可用于二分类、多分类、回归等任务&＃xff0c;是有放回抽样&＃xff0c;得到统计量的分布及置信区间。

1、基本流程&＃xff1a;对一个包含m个样本的数据集&＃xff0c;又放回地进行m次随机采样&＃xff0c;得到具有m个样本的采样集——照这样取T个这样的采样集——每个采样集训练一个基学习器——对学习器进行组合(组合时&＃xff0c;若是分类任务&＃xff0c;则使用简单投票法&＃xff0c;若是回归任务&＃xff0c;则使用简单平均法)

【注】&＃xff1a;

①算法思想是让学习算法训练多轮&＃xff0c;每轮的训练集由从初始地训练集中随机取出的m个训练样本组成&＃xff0c;某些个初始样本在某论训练集中可以出现多次/不出现。

②基于每个训练集训练一个“专属”基学习器&＃xff0c;再将这些基学习器进行加权组合。

③Bagging通过在不同数据集上训练模型&＃xff0c;降低分类器的方差(可以理解为数据集改动对模型性能的影响)&＃xff0c;防止过拟合。

2、基本性质及意义

①Bagging通过结合几个模型降低泛化误差&＃xff1a;分别训练几个不同的模型&＃xff0c;然后让所有模型表决测试样例的输出&＃xff0c;这称为模型平均&＃xff0c;采用这种策略的技术被称为集成方法。

②通过在构建模型的过程中引入随机性来减少基学习器的方差。

③因其可以减小过拟合&＃xff0c;在强分类器和复杂模型上使用时表现得很好。

④采用有放回的抽样&＃xff0c;在数据集比较小的时候可以使数据集样本“变多”&＃xff0c;因为每次训练都需要重新采样&＃xff0c;但由于有的样本可能会被选取多次&＃xff0c;相当于加大了权重&＃xff0c;改变了原本的数据分布。

3、Boosting与Bagging的比较

①样本权重&＃xff1a;Boosting有权重&＃xff0c;是根据错误率进行调整更新的&＃xff1b;而Bagging使用均匀取样&＃xff0c;每个样例的权重相等(相当于没有权重)。只能顺序生成 可以并行生成。

②样本选择&＃xff1a;Boosting每一轮的训练集不变&＃xff0c;只是训练集中每个样例在分类器中的权重发生变化&＃xff1b;Bagging的训练集是在原始集中有放回选取的&＃xff0c;从原始集中选出的各轮训练集之间是独立的。

③预测函数&＃xff1a;Boosting的弱分类器都有各自的权重&＃xff0c;分类误差小的分类器权重更大&＃xff1b;Bagging所有预测函数的权重相等。

④计算方式&＃xff1a;Boosting的权重只能顺序计算生成&＃xff1b;Bagging的权重可以并行计算生成。

⑤方差、偏差比较&＃xff1a;Boosting基于偏差的减少&＃xff1b;Bagging基于方差的减少。

&＃xff08;二&＃xff09;随机森林&＃xff1a;

1、算法概述&＃xff1a;对基学习器的每个结点&＃xff0c;先从该节点的属性集合中随机选择一个包含K个属性的子集&＃xff0c;然后从这个子集中选择一个最优属性用于划分&＃xff0c;应用于结点进行分裂【K控制了随机性的引入程度&＃xff0c;K越大&＃xff0c;随机性越大】。随机森林的基本单元是决策树。

2、每棵树的生成规则&＃xff1a;

①Bootstrap抽取样本&＃xff1a;如果训练集大小为N&＃xff0c;对于每棵树而言&＃xff0c;随机且有放回地从训练集中抽取N个训练样本&＃xff0c;作为该树的训练集。

②选属性子集&＃xff1a;若每个样本的特征维度为M&＃xff0c;指定一个m<

③努力生长&＃xff1a;每棵树都尽可能最大程度生长&＃xff0c;且无剪枝过程。

思考&＃xff1a;为什么要有放回抽样&＃xff1f;若非有放回抽样&＃xff0c;则每棵树的训练样本不同&＃xff0c;无交集&＃xff0c;这样每棵树都是“有偏的”&＃xff0c;训练出来差异大(不能有太大差异&＃xff0c;因为这些学习器解决的都是同一个问题&＃xff0c;但也不能完全没有联系&＃xff0c;这样的话学习器差异很大)&＃xff0c;而随机森林最后分类取决于多棵树(弱分类器)的投票表决&＃xff0c;应是“求同”的一个过程&＃xff0c;若用完全不同的训练集来训练则对分类结果无帮助。

3、随机森林分类效果(错误率)与两个因素有关&＃xff1a;

①森林中任意两棵树的相关性&＃xff1a;相关性越高&＃xff0c;错误率越大。

②每棵树的分类能力&＃xff1a;分类能力越大&＃xff0c;错误率越大。

4、袋外错误率&＃xff1a;

• 构建随机森林的关键问题是如何选取最优的m&＃xff0c;解决该问题主要依据计算袋外错误率(oob error,out-of-bag error)
• 可在随机森林生成的过程中对误差建立一个无偏估计&＃xff0c;因为构建每棵树时&＃xff0c;采用有放回抽样&＃xff0c;约1/3的训练实例没有参与第K棵树的生成&＃xff0c;它们便是第K棵树的oob样本。这样的采样特点便允许我们进行oob估计&＃xff1a;①对每个样本计算它作为oob样本的树对它的分类情况②以简单多数投票作为该样本的分类结果③用误分类个数占样本总数的比例作为随机森林的oob错误率。

5、随机森林的随机性体现在&＃xff1a;训练样本选择随机&＃43;属性特征选择随机。

 四、多样性增强

常见的增强个体学习器多样性的方法&＃xff1a;数据样本扰动、输入属性扰动、输出表示扰动、算法参数扰动。

1、数据样本扰动&＃xff1a;通常基于采样法(如Bagging中的自助采样、Adaboost中的序列采样)&＃xff0c;对“不稳定基学习器”很有效&＃xff1b;&＃xff08;对扰动敏感的基学习器&＃xff1a;决策树、NN&＃xff1b;不敏感的基学习器&＃xff1a;SVM、朴素贝叶斯、K近邻、线性学习器)

2、输入属性扰动&＃xff1a;不同的“子空间”(即属性子集)提供了观察数据的不同视角&＃xff0c;从不同子空间训练的个体学习集必然有所不同。算法从初始属性集中抽取出若干个属性子集&＃xff0c;再基于每个属性子集训练一个基学习器。

3、输出表示扰动&＃xff1a;对输出表示进行操作以增强多样性。可对训练个样本的类标记稍作变动&＃xff0c;如翻转法&＃xff08;flipping output&＃xff09;随机改变一些训练样本的标记等等。

4、算法参数扰动&＃xff1a;通过随机设置不同参数&＃xff0c;可产生差异较大的个体学习器。

参考&＃xff1a;

Bagging和Boosting的区别&＃xff08;面试准备&＃xff09; - Earendil - 博客园

https://blog.csdn.net/fjssharpsword/article/details/61913092