机器学习凸优化问题

1.凸集与凸函数

2.凸优化问题

3.拉格朗日乘子法

4.对偶问题,slater条件,kkt条件 

1.凸集与凸函数

凸集：在点集拓扑学与欧几里得空间中，凸集是一个点集，其中每两点之间的直线上的点都落在该点集中。千言万语不如一张图来的明白，请看下图：

凸函数：一个定义在向量空间的凸子集c(区间)上的实值函数f，如果在其定义域c上的任意两点x，y以及t∈[0,1]有： 

 

 

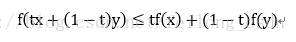
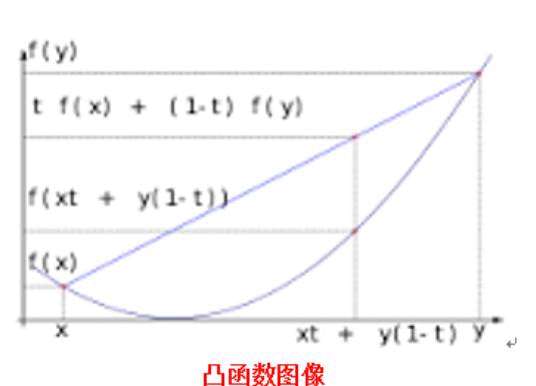
2.凸优化问题

• 凸优化：凸优化是指一种比较特殊的优化，是指求取最小值的目标函数为凸函数的一类优化问题。其中，目标函数为凸函数且定义域为凸集的优化问题称为无约束凸优化问题。而目标函数和不等式约束函数均为凸函数，等式约束函数为仿射函数，并且定义域为凸集的优化问题为约束优化问题。


• 凸优化性质： 1、目的是求取目标函数的最小（优）值； 
  2、目标函数和不等式约束函数都是凸函数，定义域是凸集； 
  3、若存在等式约束函数，则等式约束函数为仿射函数； 
  4、对于凸优化问题具有良好的性质，局部最优解便是全局最优解。

一个凸优化问题用公式描述为：

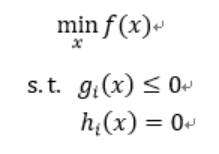
所以其目标函数f(x)以及不等式约束条件g(x)便是凸函数，而等式约束条件h(x)是仿射函数。

• 
  

  常见的几种凸优化问题

  
  
  
  
  

线性规划：如果凸优化中的目标函数ff和不等式约束条件gigi都为线性函数，那么此时的凸优化问题就成为了线性规划问题，其格式如下：

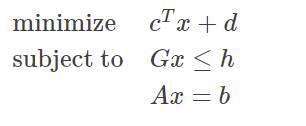
二次规划：如果凸优化中的目标函数f">ff为 二次函数，那么此时的凸优化问题就成为了二次规划问题，其格式如下：

f">　　　　　　　　　　　　　

二次约束二次规划：如果在上述二次规划中再加入一个令其不等式约束条件也为二次的，那么这时候我们称该问题为二次约束二次规划问题， 其格式如下： 

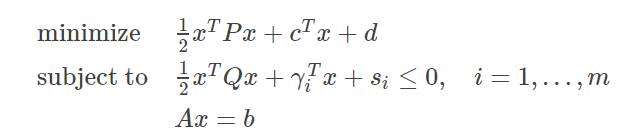
3.拉格朗日乘子法

拉格朗日乘子法的作用：求函数f(x1,x2…)在g（x1,x2…）=0的约束条件下的极值

拉格朗日乘子法的操作过程 

• 定义新函数： 

• 利用偏导方式列出以下方程

• 求解出x，y，σ的值带入f（x,y,σ）便是目标函数的极值

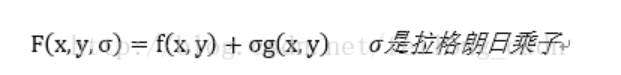
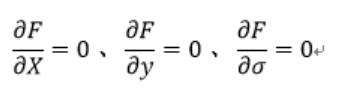
4.对偶问题,slater条件,kkt条件 

要说对偶问题，则需要从凸优化问题开始说起。假设我们现在来求解上面的那个凸优化问题的最优解：

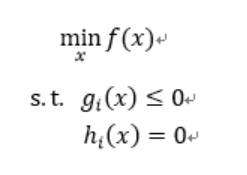
观察上面的最优化问题，便是在一定的约束条件下求解函数的极值，我们上面已经说过拉格朗日乘子法啦，所以这里便用到了。

使用拉格朗日乘子法针对上面的最优化问题有： 

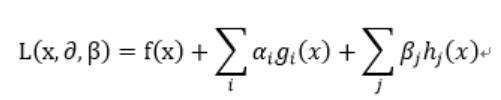
需要明确：其中α≥0、β任意，均为拉格朗日乘子，i=1,2,…,p且j=1,2,…,q

如果按照我们上面谈到的拉格朗日乘子法的思路，则应该让l(x,α,β)对x以及参数α和β进行求导，然后得出结果带入原始便可求出我们需要的最优解。

但需要注意两点： 
1、这里参数α和β总共p+q个，如果全部求偏导工作量太大，不现实； 
2、并且大家有没有想过，这个问题可能根本就没有最优解这种情况存在。

针对上面情况，我们便引出了换一种思路，那就是利用对偶问题，也就是将原问题转化成其对偶问题进行求解。

下面和大家先说一下对偶问题的基本思想，然后我们再继续从上面的问题出发，推导其对偶问题，进行求解。

对偶问题的性质：无论原命题的形式如何，对偶问题都是一个凸优化问题，还记得凸优化问题的好处吧，那就是局部最优解就是全局最优解，并且容易求解，所以我们将问题转化为其对偶问题就简化了问题的求解思路。

上面我们利用拉格朗日乘子法得到了如下式子：

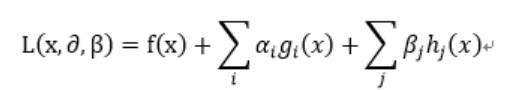
现在我们自定义一个函数如下：

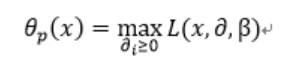
分析上面的自定义函数有：

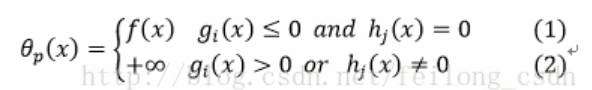
对上面的式子进行分析： 
（1）式说明，当目标函数的约束条件都满足时，则自定义的函数便是上面需要求解的目标函数f(x)，（2）则是只要目标函数的约束条件只有一个不满足，则自定义的函数便等于无穷大！

所以我们便可以认为自定义的函数θ(x) 是对原理优化问题中的约束条件进行了吸收，是原来的约束优化问题变为无约束优化问题（相对于原来变量x 无约束了），即我们可以将最初的优化问题写成： 　　　　

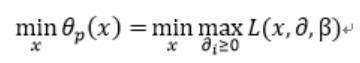
上式便是我们需要优化的原问题 
原问题的 对偶问题 便是： 

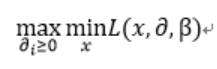
下面我们假设假命题为p，对偶问题为q！当然对偶问题已经不等价于原问题了，但是二者是存在一定联系的，下面我们来讲解二者的联系，以及如何通过求解对偶问题来得到原问题的最优解！

这里我们令： 

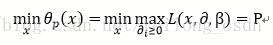
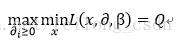
所以有： p>=q 
解释：大家想一下，函数l中最大值中最小的一个总比最小值中最大的那一个要大，也就是对偶问题提供了原问题最优值的一个下界。

但是大家想，我们是想通过对偶问题求解原问题的最优解，所以只有当二者相等时即p=q，才可能将原问题转化成对偶问题进行求解。当然，当满足一定条件的情况下，便有p=q。而这个条件便是 slater条件和ktt条件。

slater条件：

slater条件官方正规定义：存在x，使得不等式约束g(x)<=0严格成立。 
slater条件性质： slater条件是原问题p可以等价于对偶问题q的一个充分条件，该条件确保了鞍点的存在。

kkt条件：

大家已经知道slater条件已经确保了鞍点的存在，但是鞍点不一定就是最优解啊，所以kkt条件的作用便体现出来了。 
kkt条件便是确保鞍点便是原函数最优解的充分条件，当然对于我们前面举得那个例子，当原问题是凸优化问题时，则kkt条件便是鞍点便是最优解的充要条件。

kkt条件描述为一下三个条件： 

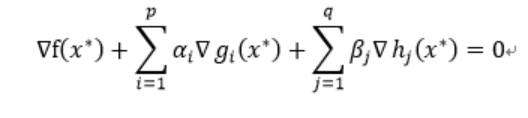
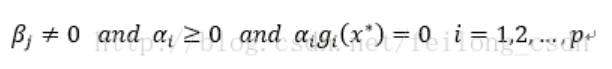
解释：第一个约束条件表明：最优点x必须满足所有等式及不等式限制条件, 也就是说最优点必须是一个可行解, 这一点自然是毋庸置疑的； 

第二个约束条件表明：在最优点x, ∇f必须是∇gi和∇hj的线性組合; 
第三个约束条件表明：拉格朗日乘子不等式的一些限制，对于不等式的拉格朗日乘子限制条件有方向性, 所以每一个α都必须大于或等于零, 而等式限制条件没有方向性，只是β不等于0。

这样对于slater条件和kkt条件都十分清楚了吧，并且也知道了他们的作用！这样我们最初的求解凸优化问题便转化为求解其对偶问题。当前我们的优化目标便是： 

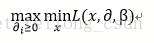
 引用以下文章：

https://blog.csdn.net/batuwuhanpei/article/details/46562459

https://blog.csdn.net/feilong_csdn/article/details/62427148