机器学习（三）处理分类以及logistic回归算法的应用

logistic回归算法

分类

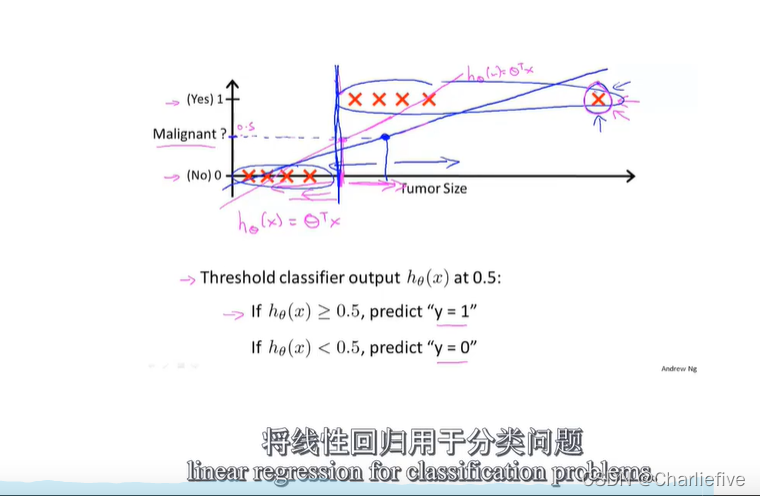
线性回归一般不用于分类问题

假设陈述

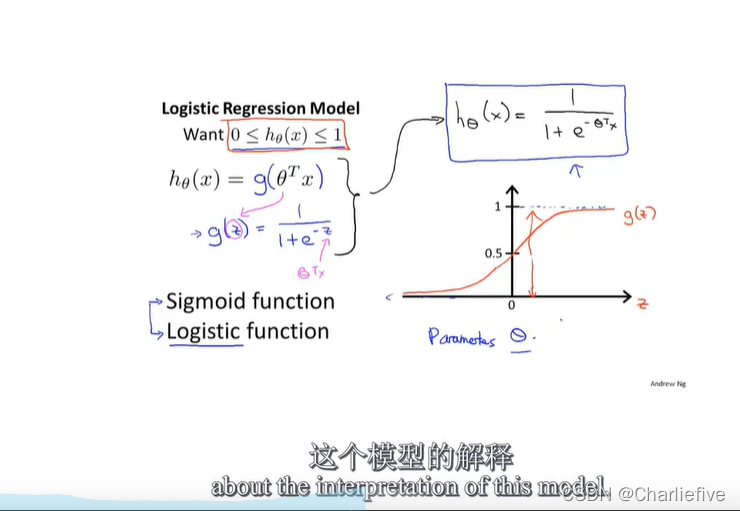
条件概率

决策界限

不同的参数，可以转化为不同的数学模型，同时也是不同的数学图像
逐步转化为概率问题。

代价函数

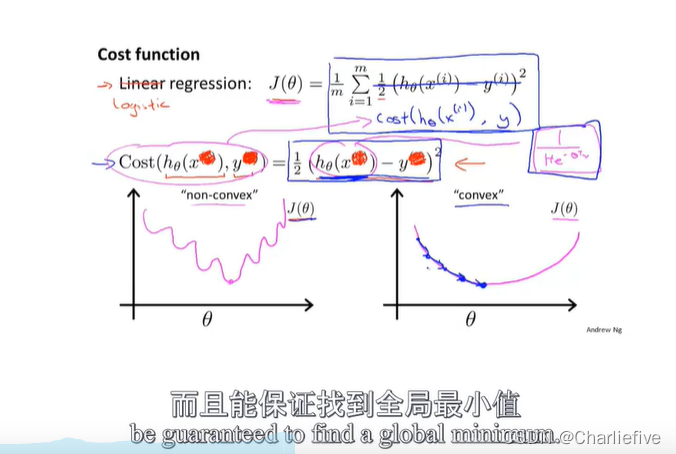
为了转化为凸优化函数，有极值

• 如果y=1（条件）且h（x）（y=1下的预测值）等于1 他俩相等，说明预测正确了，Cost（代价值）（惩罚）为0。
• 如果y=1（条件）且h（x）（y=1下的预测值）等于0 他俩完全不相等，说明预测错误了，Cost（代价值）（惩罚）为1。
  
• 如果y=0（条件）且h（x）（y=0下的预测值）等于1 他俩完全不相等，说明预测错误了，Cost（代价值）（惩罚）为1。
• 如果y=0（条件）且h（x）（y=0下的预测值）等于0 他俩完全相等，说明预测正确了，Cost（代价值）（惩罚）为0。
  

简化代价函数和梯度下降

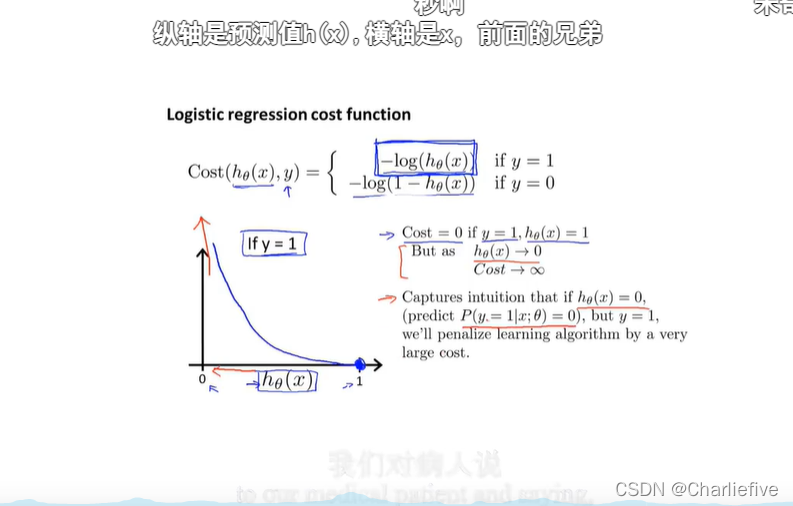
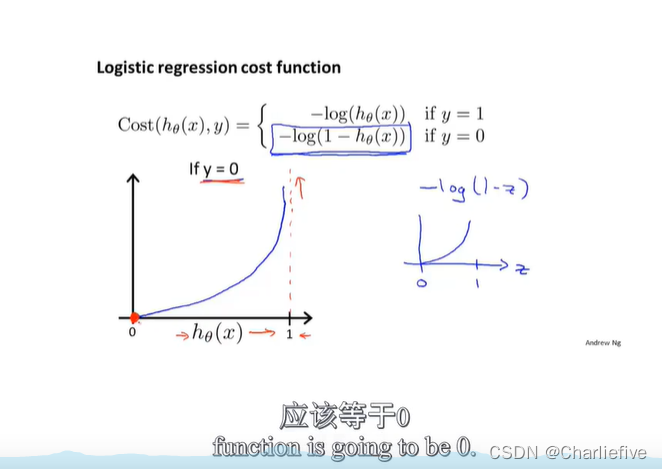
！！！这里推导很难

求导过程中的1/m整合到α里了

高级优化算法

一些算法

多元分类 一对多

将其分为三个独立的一对余的问题即可

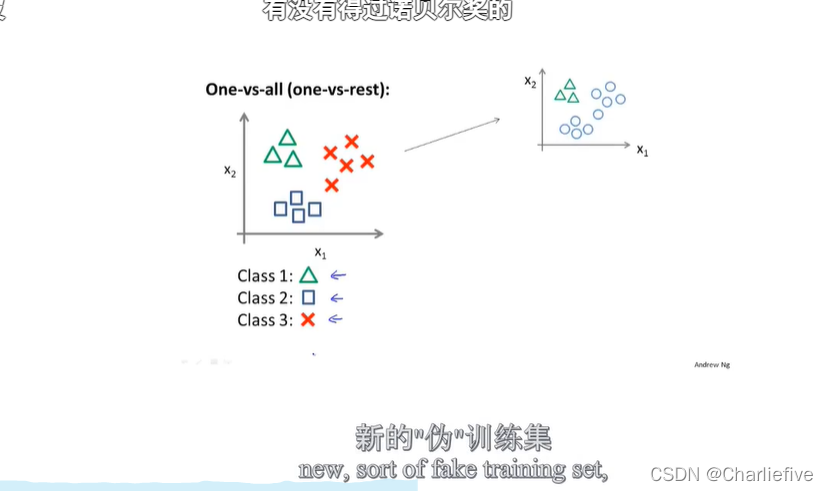
多类别分类：对每个分类找到h（thera）函数，然后选择可信度最高、效果最好的一个。

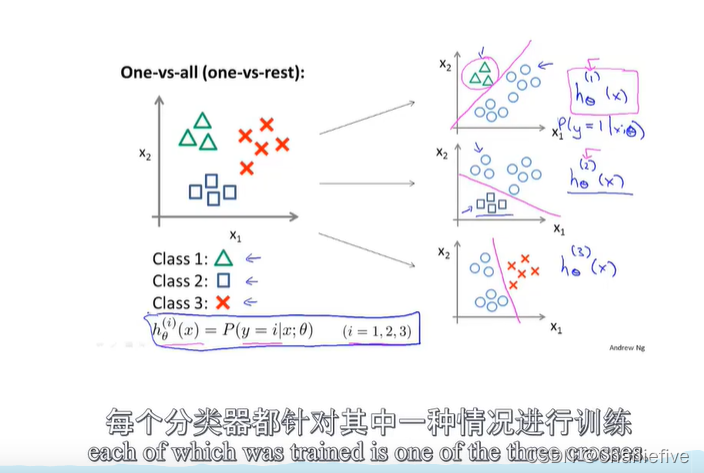
加油加油