机器学习——朴素贝叶斯与分类问题

  朴素贝叶斯：它是一种简单且强大的预测建模算法，其目的在于通过训练集学习联合分布概率$p(X,Y)$p(X,Y)。
  由贝叶斯定理可以将联合概率转换为先验概率与条件概率分布之积：$p(X=x,Y=c_k)=p(Y=c_k)p(X=c_k|Y=c_k)$p(X=x,Y=ck​)=p(Y=ck​)p(X=ck​∣Y=ck​)
  先验概率分布 $p(Y=c_k)$p(Y=ck​) 通过统计每个类别中的样本数得到，即：$p(Y=c_k)=\frac{count(Y=c_k)}{N}$p(Y=ck​)=Ncount(Y=ck​)​
  条件概率分布$p(X=x|Y=c_k)$p(X=x∣Y=ck​)则难以估计，原因在于x的量级非常巨大，即：$p(X=x,Y=c_k)=p(X_1=x_1, ... ,X_n=x_n|Y=c_k)$p(X=x,Y=ck​)=p(X1​=x1​,...,Xn​=xn​∣Y=ck​)
由上式得该条件概率分布的参数数量为指数级。
  为了解决这个问题，朴素贝叶斯法假设所有特征是条件独立的。该条件的独立性假设为：$p(X=x,Y=c_k)=p(X_1=x_1, ... ,X_n=x_n|Y=c_k)=\prod^n_{i=1}{p(X_i=x_i|Y=c_k)}$p(X=x,Y=ck​)=p(X1​=x1​,...,Xn​=xn​∣Y=ck​)=i=1∏n​p(Xi​=xi​∣Y=ck​)
  利用极大似然估计为：$p(X=x,Y=c_k)=\frac{count(X_i=x_i,y_i=c_k)}{count(y_i=c_k)}$p(X=x,Y=ck​)=count(yi​=ck​)count(Xi​=xi​,yi​=ck​)​
  公式解释：给定类别为$c_k$ck​的条件下，特征向量第$i$i维为某个特定值$x_i$xi​的概率等于类别为$c_k$ck​且第$i$i维为$x_i$xi​的样本数量除以类别$c_k$ck​下所有的样本数量。

  利用贝叶斯公式求出后验概率$p=(Y=c_k|X=x)$p=(Y=ck​∣X=x)最大的类别$c_k$ck​作为输出$y$y，公式描述如下：$y=\arg\max_{c_k}p(Y=c_k|X=x)$y=argck​max​p(Y=ck​∣X=x)
  将贝叶斯公式代入上式得：$y=\arg\max_{c_k}\frac{p(X=x|Y=c_k)p(Y=c_k)}{p(X=x)}$y=argck​max​p(X=x)p(X=x∣Y=ck​)p(Y=ck​)​
  由于分母$p(X=x)$p(X=x)与$c_k$ck​无关，在求最大后验概率可省略，即：$y=\arg\max_{c_k}p(X=x|Y=c_k)p(Y=c_k)$y=argck​max​p(X=x∣Y=ck​)p(Y=ck​)
  将前文中得独立性假设带入上式中，得：$y=\arg\max_{c_k}p(Y=c_k)\prod_{i=0}^np(X_i=x_i|Y=c_k))$y=argck​max​p(Y=ck​)i=0∏n​p(Xi​=xi​∣Y=ck​))
  此时只要求得先验概率分布 $p(Y=c_k)$p(Y=ck​)与条件概率分布$p(X=x|Y=c_k)$p(X=x∣Y=ck​)即可得出结果。

  朴素贝叶斯之所以朴素，是因为它假设每个输入变量是独立的。虽然这个假设在实际生活中出现的频率不多，朴素贝叶斯算法对于绝大部分的复杂问题仍然有效。

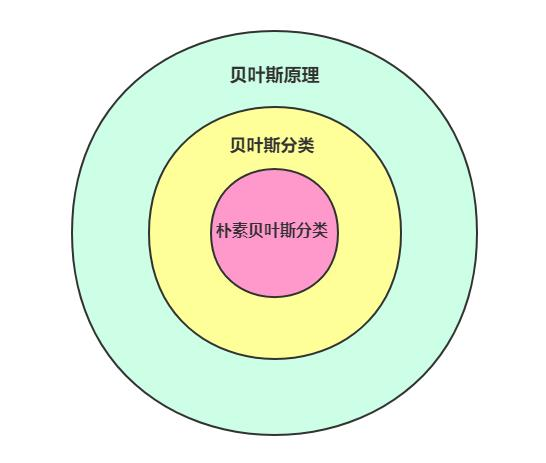
贝叶斯定理、贝叶斯分类器与朴素贝叶斯分类器三者的关系：贝叶斯原理为数学模型，是基础。在此数学基础上设计出了贝叶斯分类。而朴素贝叶斯分类则为贝叶斯分类中的一个具体实现方法。

朴素贝叶斯分类器基本思想：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。
贝叶斯分类器工作流程：工作流程大体分为三个阶段：准备阶段、分类器训练阶段、应用阶段。如下图所示：

贝叶斯算法的优缺点

  优点：
    （1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率，常用于文本分类。
    （2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，当数据量超出内存时，可以采采取增量训练。
    （3）对缺失数据不敏感，算法也比较简单。
  缺点：
    （1）理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。
    （2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
    （3）由先验概率来决定后验概率，存在错误率。

参考引用

《统计学习方法》李航 著
《自然语言处理入门》何晗 著
朴素贝叶斯分类——guoyunfei20
朴素贝叶斯分类:原理——qiu_zhi_liao