机器学习基石第二周

1.感知机与其假设空间

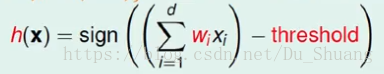
假设输入为X&＃xff0c;X是个多维向量分量为x1,x2,…..,xi。比如X是个银行的客户&＃xff0c;x1,x2,……xi,就分别代表那个人的性别&＃xff0c;年您&＃xff0c;职业&＃xff0c;收入等信息。感知机就是对这些分量进行加权求和&＃xff0c;并设定一个阈值&＃xff0c;如果求和结果大于这个阈值&＃xff0c;那么输出一个结果&＃xff0c;如果为负&＃xff0c;则输出相反的结果。这里的权重组&＃xff0c;与阈值的组合有无穷多种&＃xff0c;我们将这些组合的集合称作假设空间H。我们的目的就是从H中学到一个最接近理想函数f的h。

我们将阈值乘以1&＃xff0c;并将这个1当做X的第0维向量&＃xff0c;那么这个阈值就相当于第0维的权值&＃xff0c;最后将权值向量化&＃xff0c;得到化简后的结果。

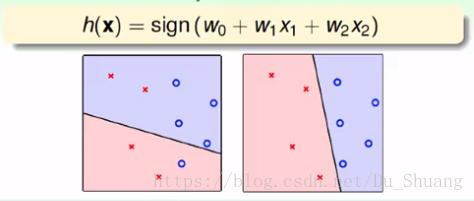
假设X所代表的向量只有二维&＃xff0c;则每个输入X相当于平面上的一个点&＃xff0c;而权值向量与输入向量的乘积相当于平面上的一条线&＃xff0c;当点落在线上&＃xff0c;则结果为0&＃xff0c;如果在上方则大于零&＃xff0c;下方则小于零。这就是感知机的集合表示。

那么问题的关键就是我们怎么从假设空间中找出一条最接近理想线条f的g呢&＃xff1f;
要想让g接近于f那么至少在我们看过的数据里面&＃xff0c;g要和f有相同的效果&＃xff0c;所以我们要的g要求对以前的所有数据进行正确的分类。

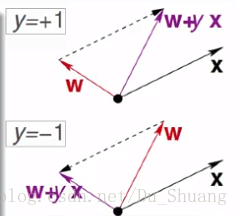
那我们该怎么做呢&＃xff1f;
1.首先我们随便确定一个权重系数和阈值即W0。当然这个肯定不是我们想要的系数。因为它会对以前的数据进行错误的判断。比如对于X0&＃xff0c;实际的结果应该是正的&＃xff0c;而W0的输出确是负的&＃xff0c;那么证明W0是远离于理想函数f的&＃xff0c;那么我们就得对它进行更改&＃xff0c;如果正的判断成了负的那么说明W0与X0的夹角太大&＃xff0c;这时我们就缩小其夹角&＃xff0c;使其变为正数&＃xff0c;反之则增大其夹角使之变为负数。这里我们的改变方法是在W0的基础上加上或者减去判断错误的那个输入。一直重复循环直到没有错误。
但是有一个问题&＃xff0c;那就是每次只检测一个样本&＃xff0c;所以会捡了芝麻而丢了西瓜&＃xff0c;所以会这个样本对了&＃xff0c;而另一个样本点又错了&＃xff0c;所以这个算法会计算很多次后才会分类正确。

上面只是定性的对这个问题做了一个简单的叙述&＃xff0c;下面将对这个问题进行数学的证明&＃xff1a;

这里面假设Wf为我们理想的f所具备的系数&＃xff0c;Wt&＃43;1为每次更新之后的系数。Wf*Wt&＃43;1越大证明更新之后的值与理想的系数越接近。上图表示不论数据对错每次迭代更新后系数都越来越接近理想值。
但是这个增大不一定就是角度接近导致的增大&＃xff0c;还有可能是向量膜变化导致的结果增大&＃xff0c;这就是我们接下来要讨论的问题。

在更新的时候我们只会对错误的数据进行更新&＃xff0c;如上图所示&＃xff0c;这就导致更新之后Wt&＃43;1的模不会太大于Wt的模甚至小于Wt的模&＃xff0c;所以我们能确定Wt&＃43;1与Wf的接近是因为角度的接近所导致的。

但是之前我们的假设是该数据是线型可分的即一定能找到一条直线能够将这些数据点划分开来&＃xff0c;但是如果数据是不可分的呢&＃xff1f;我们该怎么办&＃xff1f;

那我们就找一条所犯错误最小的直线对其进行分化。

具体思路是&＃xff1a;我们首先随便初始化一条分割线&＃xff0c;然后随机选择一个数据点对其进行更新&＃xff0c;当且仅但新得到的分割线所犯错误小于之前的才对其进行更新&＃xff0c;直到达到规定的次数或者要求时我们才停止算法&＃xff0c;这就是所谓了pocket算法&＃xff0c;不过该算法相比于PLA要慢很多&＃xff0c;因为每次更新后我们都要对其进行验证&＃xff0c;并且如果数据线型可分&＃xff0c;当找到最好的线之后&＃xff0c;它并不会停止&＃xff0c;而是会继续进行更新。