概率图模型中的条件概率分布(CPD)详解

条件概率分布（Conditional Probability Distribution, CPD）是概率图模型中的基础概念，它描述了一个或多个随机变量在给定某些条件下的概率分布。在概率图模型中，通过定义随机变量间的条件关系，能够有效地建模复杂系统的不确定性。

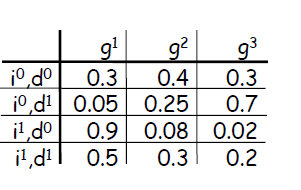
对于简单的条件概率问题，可以通过条件概率表（CPT）来直观地展示。例如，图1展示了p(g|i,d)的条件概率分布，其中i和d分别有两个取值，构成一个伯努利分布。然而，当条件变量的数量增加时，如每个变量有六个可能的取值，条件概率表的大小将迅速膨胀至6^2个条目，这不仅难以管理和计算，也不符合实际应用的需求。

在更复杂的场景下，如医学诊断中，多个潜在原因可能导致同一症状，此时条件概率表的大小将呈指数级增长，达到2^N个条目，N为原因的数量。因此，寻找有效的方法来简化条件概率分布的表示变得尤为重要。

为了应对这一挑战，研究者们提出了多种方法来简化CPD的表达。其中，树状结构的CPD是一种有效的解决方案，它通过将多个条件变量按照重要性排序，形成一个层次结构，从而减少所需的概率条目数量。例如，在工作选择的情境中，首先考虑教育背景，其次是外貌，最后是智力，这样可以将原本复杂的多变量依赖关系简化为一个有序的序列。

2. 片选CPD (Multiplexer CPD)

片选CPD适用于这样的情况：当一个随机变量A被确定后，另一个随机变量Y的取值仅与A的一个特定父节点相关。例如，在空中交通管理中，当雷达锁定一架特定飞机时，该飞机的速度（Y）仅与其自身的速度数据相关，而与其他飞机的速度无关。这种情况下，条件概率可以简化为：

3. 噪声或CPD (Noise OR CPD)

噪声或CPD用于处理多因素导致某一结果的情况，其中各因素之间存在一定的不确定性和噪声。例如，咳嗽可能由多种原因引起，但并非所有原因都会直接导致咳嗽。在这种情况下，咳嗽的概率可以通过计算各因素不导致咳嗽的概率的乘积，再用1减去这个乘积来得到。

此外，这种逻辑运算还可以扩展到其他形式，如“与”操作或取最大值等，以适应不同的应用场景。

4. Sigmoid CPD

Sigmoid CPD在处理多因素影响某一结果时特别有用。例如，个人魅力（如是否能找到伴侣）可能受到多个因素的影响，包括外貌、性格等。这些因素可以赋予不同的权重，并通过Sigmoid函数转换为最终的概率值。

5. 线性高斯CPD

在线性高斯CPD中，随机变量通常被视为连续变量，而不是离散变量。例如，机器人通过多个传感器测量距离墙壁的距离（Xi），最终需要融合这些数据来估计真实距离（Y）。这种情况下，可以使用线性高斯模型来表示Y的概率分布。

值得注意的是，所有输入变量X也可以是高斯分布的，但Y的方差假设不受X方差的影响。

6. 总结

本章讨论了如何通过不同的方法来简化多变量条件概率的表达，从而提高概率图模型的效率和可解释性。通过引入树状结构的CPD、片选CPD、噪声或CPD、Sigmoid CPD以及线性高斯CPD等技术，可以在保持模型准确性的同时，显著减少计算复杂度。