机器学习笔记—正则化和模型选择

如果针对某个学习问题，从众多模型中选择一个模型，能够在偏差和方差中做一个平衡，怎么样才能自动选择呢？例如，使用多项式回归模型 h(x)=g(θ₀+θ₁x+θ₂x²+...+θ_kx^k)，想自动决定 k 的值，在 0~10 之间选择。再比如，要自动选择局部权重回归中的带宽参数 τ，或者 L1 正则化 SVM 的参数 C，怎么做呢？

设有有限个模型 M={M₁,...,M_d} 供选择，例如在上面的例子中，M 可以是一个 i 项式回归模型。如果想要在 SVM、神经网络和 Logistic 回归之间选择，M 可以包含这些模型。

1、交叉验证

设有训练集 S，给个看起来像个算法的方法，这是用经验风险最小化来进行模型选择的结果。

a. 在 S 上训练每个模型 M_i，来获得一些假设 h_i。

b. 选择有最小训练误差的假设。

这个方法不行。考虑多项式的阶，阶数越多，它就越能更好地拟合训练集 S，训练误差越小，当然方差也越大，这个方法倾向于选择阶数很高、性能很差的模型。

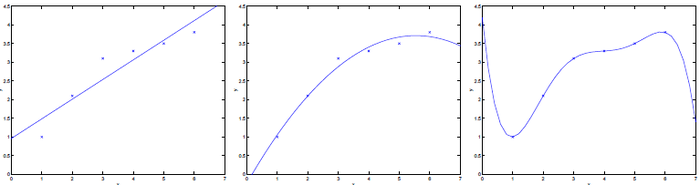
这里有个更好的算法， 保留交叉验证：

a. 将 S 随机地分成 S_train (约 70%) 和 S_cv (约 30%)，这里，S_cv 被称为保留交叉验证集。

b. 在 S 上训练每个模型 M_i，得到一些假设 h_i。

c. 选择在验证集 S_cv 有最小误差 ε^{^}(h_i) 的 h_i。

在模型没有训练过的验证集 S_cv 上进行测试，能够对 h_i 的真实泛化误差有一个更好的估计，然后选择最小泛化误差。通常 1/4~1/3 的数据用来做验证集，30% 用得较多。

上面第三步也可以替换成，根据 min_iε^{^}(h_i) 选择模型 M_i，然后在整个训练集 S 上重新训练模型 M_i，除非学习算法对初始条件或数据的变动很敏感，那就最好不要重新训练。

保留交叉验证的缺点是它浪费了 30% 的数据，即使最后在整个数据集上重新训练了数据，在选择学习算法时依然只用了 0.7m 的数据。数据量大了还行，数据量很小就不行了，比如 m=20。

这里有个方法，称为 k 重交叉验证，每次保留少量数据：

a. 将 S 随机分成 k 个不相交的子集，每个子集包含 m/k 个训练例子，这些子集标记为 S₁,...,S_k；

b. 对每个模型 M_i，我们通过以下方式评估：

对于 j=1,...,k

在 S₁∪...S_j=1∪S_j+1∪...S_k (在所有数据上除了 S_j)上训练模型 M_i，从而得到假设 h_ij，然后在 S_j 上测试 h_ij，得到

模型 M_i 的估计泛化误差为 ε^{^}_Sj(h_ij) 的均值（对每个 j 作平均）

c. 选择最小估计泛化误差的 M_i，然后在整个训练集 S 上重新训练，最终输出的结果假设就是答案。

k 一般为 10，现在每次保留的数据是 1/k，比之前少多了，但是计算量大了，因为每个模型都要训练 k 次。如果数据量确实太小，有时就选择 k=m，这种方法叫留一交叉验证。

 

2、特征选择

模型选择的一个特例是特征选择，假设有一个监督学习问题，特征个数非常大(n>>m)，但你怀疑只有一部分特征跟学习任务有关。即使在 n 个特征上使用简单的线性分类器（如感知机），假设类的 VC 维也依然是 O(n)，所以欠拟合将成为一个潜在的问题，除非训练集非常大。

这种情况要用降维算法来减少特征个数，给定 n 个特征，就有 2ⁿ 个可能的特征子集，所以特征选择就变成 2ⁿ 个模型的模型选择问题，对于很大的 n 值，要去遍历和比较所有的 2ⁿ 个模型，计算量就非常大，所以要用一些启发式搜索过程来找到一个好的特征子集，下面的搜索过程被称为前向搜索：

a. 初始化 F=∅

b. 重复 {

    1. 对于 i=1,...,n ，如果 i∉F，那么令 F_i=F∪{i}，并且使用交叉验证来评估特征集 F。

    2. 令 F 为上一步中找到的最好的特征子集。

}

c. 选择整个搜索过程中的最好的特征子集。

算法的终止时间可以定为 F={1,...,n}，或者 |F| 超过预先设置的阈值（跟你算法要使用的最大特征个数有关）。

这个算法是包装模型特征选择的一个实例，因为它是个包装学习算法的过程，不停地验证不同的特征子集。

除了前向搜索，还有其它搜索过程，如后向搜索，起始 F={1,...,n} 是所有特征的集合，重复每次删除一个特征直到 F=∅。

包装特征选择算法运行效果不错，但太耗费计算量了，完整的前向搜索（当 F={1,...,n} 时终止）的时间复杂度为 O(n²)。

过滤特征选择是一个启发式的，易于计算的方法，也是通过选择特征子集。思想是计算每个特征的分数 S(i)，测量每个特征 x_i 有关类标识 y 的信息量。然后，选择分数 S(i) 最高的 k 个特征。

可以把定义 S(i) 为 x_i 和 y 的相关性，最后选择同类标识最相关的特征。实践中，对于离散值特征 x_i，定义 S(i) 为 x_i 和 y 之间的互信息 MI(x_i,y)。

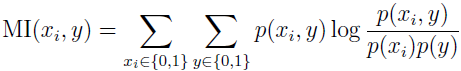
这个方程假设 x_i 和 y 都是二值的，在变量的定义域里求和。p(x_i,y)，p(x_i) 和 p(y) 都能根据训练集中它们的经验分布来估计。

为了理解分数的含义，把互信息表示成 Kullback-Leibler (KL) 距离的形式。

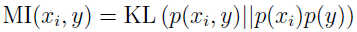非正式的，这是一种测量概率分布 p(x_i,y) 和p(x_i)p(y) 不同程度的方法。如果 x 和 y 是独立的随机变量，那么 p(x_i,y)=p(x_i)p(y) ，它们的 KL 距离是 0，也就是说，x_i 没有关于 y 的任何信息，所以分数 S(i) 很小，反之，如果 x_i 有关于 y 的很多信息，那么它们的互信息 MI(x_i,y) 就非常大。

最后，根据分数 S(i) 对特征排序，怎么决定选择多少个特征？一个标准方法是使用交叉验证来从 k 的不同值中选择。例如，使用朴素贝叶斯来对文本分类时，一个问题是词汇个数 n 通常很大，使用这种方法来选择特征子集会增加分类准确性。

 

3、贝叶斯统计和正则化

下面再介绍一个防止过拟合的工具。

之前的章节，使用最大似然估计（ML）来拟合参数，选择参数根据

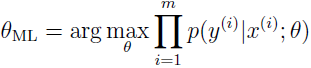
通过后续的讨论，我们把 θ 看作未知的参数，频率统计学家把 θ 看作是定值但未知的，我们的工作就是通过统计过程（如最大似然）来试图估计这个参数。

另一种参数估计的方法是采用贝叶斯观点，认为 θ 是值未知的随机变量，在这种方法中，指定先验分布 p(θ) 来表明参数的先验信念。给定训练集 S={(x⁽ⁱ⁾,y⁽ⁱ⁾),i=1,...,m}，当对新值 x 做预测时，我们可以计算参数的后验分布

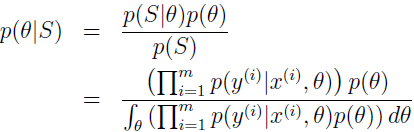
在上面的方程中，p(x⁽ⁱ⁾|y⁽ⁱ⁾,θ) 来自学习算法所用的模型。例如，如果用的是贝叶斯 Logistic 回归，那么

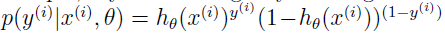
其中

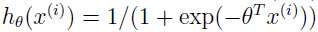
当给定新的例子 x 并对其做预测，就要用 θ 的后验分布来计算类标识的后验分布。

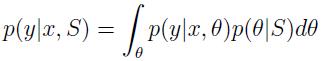
其中，p(θ|S) 来自上面的方程，所以，如果目标是给定 x 来预测 y，那么就输出

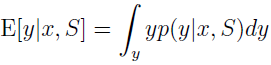
这个过程是“完全贝叶斯”预测，预测是以 θ 的后验概率 p(θ|S) 为参数的均值。不过，通常很难计算后验分布，因为它在 θ（通常维数很高） 上取积分，这往往是一个 NP 难问题。

所以在实践中，以对 θ 近似取后验分布代替。一个常用的近似是把对 θ 的后验分布以单点估计来近似，对 θ 的最大后验（MAP,Maximum a posterior）为：

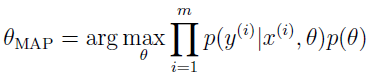
注意这个式子跟 θ 的最大似然区别在于后面多了个 p(θ)。

在实际应用中，对先验 p(θ) 一个常用的选择是假定 θ~N(0,τ²I)。使用这个先验，拟合参数 θ_MAP 将比最大似然有更小的范数。实际上，这将使参数的贝叶斯 MAP 估计比 ML 的最大似然估计更少的过拟合。例如贝叶斯 Logistic 回归对于文本分类就是一个很有效的算法，即使 n>>m。

 

参考资料：

1、http://cs229.stanford.edu/notes/cs229-notes5.pdf

2、http://blog.csdn.net/stdcoutzyx/article/details/18500441