到目前为止,我们主要学习了学习算法模型: 得到最大似然估计值:
得到最大似然估计值:
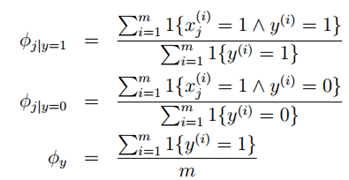
φj|y=1 的分子表示,遍历所有样本,寻找标签y=1也就是垃圾邮件中j词语出现的次数,分母表示训练集合中垃圾邮件的总数。总的式子就表示在垃圾邮件中j词语出现的概率。
同理,φj|y=0 表示在非垃圾邮件中j词语出现的概率。
φy表示垃圾邮件占所有样本样件总数的比例。
其中的
由于NIPS从未在垃圾邮件和正常邮件中出现过,所以结果只能是0了。于是最后的后验概率:
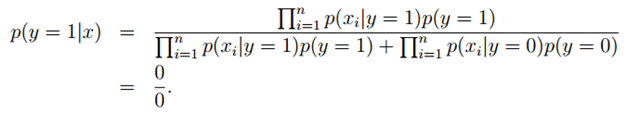
对于这样的情况,我们可以采用拉普拉斯平滑,是假设每个特征值都出现过一次,对于未出现的特征,我们赋予一个小的值而不是0。具体平滑方法为:
假设离散随机变量取值为{1,2,···,k},原来的估计公式(某个结果出现的次数在总试验次数中的比例)为:
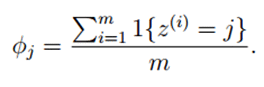
使用拉普拉斯平滑后,新的估计公式为:
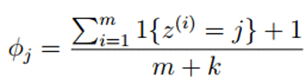
即每个k值出现次数加1,分母总的加k,类似于NLP中的平滑,具体参考宗成庆老师的《统计自然语言处理》一书。
对于上述的朴素贝叶斯模型,参数计算公式改为:
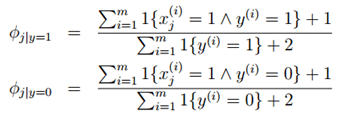
example:
A队和别人打比赛,在过去的样本中,A和B打了两次,输了两次,A和C打了两次,输了两次,A和D打了一次,输了一次,问现在A和E打赢得概率:
如果不用拉普拉斯平滑算出来最后A和E打肯定输,但是是不合常理的。我们进行平滑后的计算:
P(y=1)= (赢的概率)/(总场数输+赢)
平滑就是假设已经输了一局赢了一局,所以目前:
P(y=1)= 0+1/5+1+1=1/7.
3.4 多项式事件模型(NB-MEM(multinomial event model),向量x表示一个邮件)
对 3.2 提到的NB-MBEM模型目前有很多的扩展。比如将每个分量多值化,即将P(x|y)由伯努利分布扩展到多项式分布;再比如将连续变量值离散化(分段表示)。
目前将介绍第一种,也就是将P(x|y)由伯努利分布扩展到多项式分布。这是与多元伯努利事件模型(NB-MBEM)有较大区别的NB模型,即多项式事件模型(multinomial event model,NB-MEM)。
首先,NB-MBEM中的特种向量x的每个分量代表词典中该索引上的词语在本文中是否出现过,取值范围为{0,1},特征向量的长度为词典的大小;而在NB-MEM中,特征向量x的每个分量的值使文本中处于该分量的位置的词语在词典中的索引,其取值范围是{1,2,....|V|}.|V|表示词典的大小,特征向量的长度为相应样例文本中词语的数目。
example:
NB-MBEM:一篇文档的特征向量可能如下所示,表示一封邮件中出现了a和buy这两个词:
 ,n可以变化,因为每封邮件的词的个数不同。然后我们对于每个xi随机从|V|个值中取一个,这样就形成了一封邮件。这相当于重复投掷|V|面的骰子,将观察值记录下来就形成了一封邮件。当然每个面的概率服从p(xi|y),而且每次试验条件独立。这样我们得到的邮件概率是
,n可以变化,因为每封邮件的词的个数不同。然后我们对于每个xi随机从|V|个值中取一个,这样就形成了一封邮件。这相当于重复投掷|V|面的骰子,将观察值记录下来就形成了一封邮件。当然每个面的概率服从p(xi|y),而且每次试验条件独立。这样我们得到的邮件概率是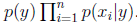 。居然跟上面的一样,那么不同点在哪呢?注意第一个的n是字典中的全部的词,下面这个n是邮件中的词个数。上面xi表示一个词是否出现,只有0和1两个值,两者概率和为1。下面的xi表示|V|中的一个值,|V|个p(xi|y)相加和为1。是多值二项分布模型。上面的x向量都是0/1值,下面的x的向量都是字典中的位置。
。居然跟上面的一样,那么不同点在哪呢?注意第一个的n是字典中的全部的词,下面这个n是邮件中的词个数。上面xi表示一个词是否出现,只有0和1两个值,两者概率和为1。下面的xi表示|V|中的一个值,|V|个p(xi|y)相加和为1。是多值二项分布模型。上面的x向量都是0/1值,下面的x的向量都是字典中的位置。
形式化表示为:
m个训练样本表示为:![clip_image077[6] clip_image077[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/c8f535106725e2cb.png)
![clip_image078[6] clip_image078[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/c1881690d0038aa4.png)
![clip_image079[6] clip_image079[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/6ec81dd1dedfeb36.png)
表示第i个样本中,共有ni个词,每个词在字典中的编号为![clip_image080[6] clip_image080[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/71111c204508dcec.png) 。
。
那么我们仍然按照朴素贝叶斯的方法求得最大似然估计概率为
![clip_image081[6] clip_image081[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/656882b123be2bdd.png)
其中P(y)表示是垃圾邮件的概率。在p(y)的前提下向你发送特殊关键词的概率。n表示的是邮件词的个数,m是总样本数。
解得,
![clip_image082[6] clip_image082[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/8914c489acf9e0a5.png)
φk|y=1表示某人向你发送垃圾邮件时,他们会选择垃圾邮件出现的下一个词是k的概率。分子表示在样本中词k出现在垃圾邮件的次数。分母表示样本邮件中垃圾邮件所有词的总数。
φk|y=0表示某人向你发送非垃圾邮件时,他们会选择非垃圾邮件出现的下一个词是k的概率。
φy垃圾邮件占总样本的比例。
举个例子:(http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971903.html)
此时|V|=3,n1=n2=2,n3=n4=3,m为总试验次数。
假如邮件中只有a,b,c这三词,他们在词典的位置分别是1,2,3,前两封邮件都只有2个词,后两封有3个词。
Y=1是垃圾邮件。
那么,
![clip_image084[6] clip_image084[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/c0addaa19758f603.png) (在y=1的情况下出现x1-x3特征的次数所占出现词总数的比例)
(在y=1的情况下出现x1-x3特征的次数所占出现词总数的比例)
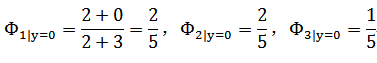 (在y=0的情况下出现x1-x3特征的次数所占出现词总数的比例)
(在y=0的情况下出现x1-x3特征的次数所占出现词总数的比例)
![clip_image088[6] clip_image088[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/cfeb9d83588873cc.png)
假如新来一封邮件为b,c那么特征表示为{2,3}。
那么
![clip_image090[6] clip_image090[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/9dafa9003ded113b.png)
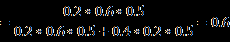
那么该邮件是垃圾邮件概率是0.6。
注意这个公式与朴素贝叶斯的不同在于这里针对整体样本求的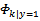 ,而朴素贝叶斯里面针对每个特征求的
,而朴素贝叶斯里面针对每个特征求的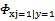 ,而且这里的特征值维度是参差不齐的。
,而且这里的特征值维度是参差不齐的。
这里如果假如拉普拉斯平滑,得到公式为:
![clip_image097[6] clip_image097[6]](https://img8.php1.cn/3cdc5/15ac2/5a0/32b0aa6203353e81.png)
表示每个k值至少发生过一次。注意这里分母加的是字典的总数,表示这个词在这个字典中出现过一次。
另外朴素贝叶斯虽然有时候不是最好的分类方法,但它简单有效,而且速度快。