红黑树插入算法(一)

前言

红黑树在数据结构里面,是一种能自动平衡的树,它的查询速度很快,因为能够用到二分法,二分法的查询复杂度只有O(log2(N)),几万条的数据也就只需查十几次,不过要维持那么高的查询速度也是有代价,它的添加和删除节点都需要每次都保证平衡.下面就开始介绍一它的节点添加算法.

一.红黑树的定义

我们先来介绍一下红黑树的特点,首先,红黑树必须满足下面的5个条件:
• 1.节点是红色或黑色。
• 2.根是黑色。
• 3.所有叶子都是黑色（叶子是NIL节点）。
• 4.每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
• 5.从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点（简称黑高）

以上是红黑树必须满足的条件,如果有一条不满足它就变成一个普通的树,所以需要保证每次添加或删除节点都能满足以上要求.

另外红黑树还有一个特点,红黑树和平均树不一样,它的高度其实并不非常的平均,不过它的最高的高度永远都不会超过它的最矮的高度的两倍.为什么呢?下面就来看一下一个最极端的红黑树:

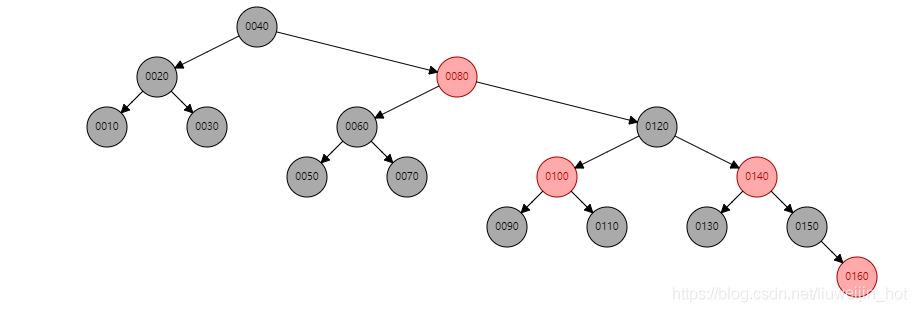
上图的红黑树,我很容易可以看出来,上面最短的高度是最左边的节点那里,全部都是黑色的,最右边的高度是最长的,我们知道红黑树的任何节点出发必须满足每个黑色节点数量一致.所以如果我们要它的某一边高度尽可能的长,我们就只能插入红色节点,不能插入黑色节点,那我们能够插入最多的红节点,我们只能在每个黑色的节点下面再加多一个红节点,并且一个黑节点只能加最多一个红节点,因为红黑树第4点已经提到,
红节点的节点不能是红节点.所以它最长的数量是 n个黑节点+n个红节点=2n个节点.

二.插入算法实现

首先先来介绍一下红黑树的平衡手段.

1.节点旋转;
2.节点变色

节点旋转
旋转是所有树的一种特点,它分为左旋和右旋转两种:

左旋转

右旋转

还有一种情况是不能直接旋转的,列如下面的这种情况:
在这里插入图片描述

假如我要在节点30后面插入一个35的节点,是直接旋转不了的,不过并不代我们对它完全没有办法,我们可以通过下面间接的旋转,先将节点30和35调换位置,然后再让35和40右旋转

节点变色
节点也是可以改变两边的平衡的,下图,左边是不平衡的,右边是平衡的,它们的结构完全没有变化,就只该变了节点.那插入新的节点的时候是红色的?

原因是插入之前所有的节点都是平衡的,如果插入黑色节点,会100%打破平衡.如果插入的是红色的节点只有50%情况会打破平衡.

上面说完了平衡节点的两种方式,下面再来说一下插入的流程.
I.首先找到要插入的节点位置,作为当前节点

II.插入节点
----1.当前节点为黑色，插入红色节点到到当前子节点，无需变色和旋转。
----2.当前节点为红色：
------21.如果当前节点和它的兄弟节点为红色，将当前节点和它兄弟节点变为黑色，如果父节点不是根节点，变为红色。
------------211.变完色之后，如果祖父节点为红色，然后把祖父节点作为当前节点跳到步骤2(递归)。
------22.当前节点的兄弟节点为黑色，当前节点变黑色，父节点变红色，当前节点跳到步骤3。
----3.如果能旋转，则进行左旋或右旋，不能旋转则将当前节点的位置与子节点对换，再作旋转。

树的查找就不多解释了,就是一个个值比对,直到找到叶节点.

1.首先我们需要归纳一下下图中标记黑色箭头的都是在黑色节点上可以插入新节点的地方

虽然在不同的节点上,但它的结构其实只有下面这种,当我们插入红色的节点,对它的平衡来说完全没有改变.

所以我们可以归纳出通用的一步:1当前节点为黑色，插入红色节点到到当前子节点，无需变色和旋转。

2当我们插入的是红色节点时,这种情况比较多,因为红黑不能存在有两个连续的节点,所以我们插入新节点是要判断怎么变色和旋转.下面标出我们能够插入的红色节点的位置.

我来归纳一下一共有5种情况:

当我们要插入的那个节点,它的兄弟节点也是红色,我有4个位置可插入

但其实四个位置都是一样的,因为它是对称的,不管插入到那个子节点上,都只需要改被插入节点及其父节点和兄弟节点的颜色就行

所以我们又归纳出了第二条规律:21.如果当前节点和它的兄弟节点为红色，将当前节点和它兄弟节点变为黑色，如果父节点不是根节点，变为红色。

下面我们来分析这种情况,首先整个节点是没有兄弟节点的,但是我们可以吧nil节点看作是黑色的,所以它有一个黑色的兄弟节点

当我们把节点插到它右边时,它是没法一口气做旋转的,所以我们将旋转抽象为一个独立的步骤:3.如果能旋转，则进行左旋或右旋，不能旋转则将当前节点的位置与子节点对换，再作旋转。
下面这个图是将节点31与节点38对调了位置,再与节点45做旋转.

当我们把节点插入到左边时

其实上面两种情况其实也一样,现在我们又能得出另外一种结论:22.当前节点的兄弟节点为黑色，当前节点变黑色，父节点变红色，当前节点跳到步骤3。(我截的图是先旋转再变色,这里是先变色再旋转其实结果一样)

来我们接着继续分析,这个的兄弟节点也是黑色的,所以和上面的条件是一样的,那我们看看,结果是不是也一样

插入新节点到左边:

插入到右边节点:

步骤22仍然适用这种场景

再看看下面这种场景是不是一样

插入到左节点

插入到右节点

一样适用步骤22

最后下面这种情况也也一样

所以我们的算法只需要考虑下面两种情况,其他的都是它们的变形:

不过两个节点相同的还有一种情况要考虑,就使它的祖父节点为红色时:


所以需要将在步骤21处理后,再补充一点:211.变完色之后，如果祖父节点为红色，然后把祖父节点作为当前节点跳到步骤2(递归)。
就21点需要考虑递归问题,其步骤不需要,因为调整完之后,父节点还是黑色的,和原来没啥不一样.

结语

红黑树的插入算法讲完了,因为删除节点和插入节点的算法是不对称的,而且要复杂得多,后面本人再继续完善删除算法.