好用的综合bim插件：Revit属性对话框中“视图范围”命令的使用

　　好用的综合bim插件&＃xff1a;Revit属性对话框中“视图范围”命令的使用

　　每个平面图都具有视图范围属性&＃xff0c;也称为可见范围。视图范围是一组水平平面&＃xff0c;可以控制视图中对象的可见性和外观。水平面为顶部平面、剖切面和底部平面。顶部切割平面和底部切割平面表示视图范围的顶部和底部。剖切面是确定视图中某些图元可视剖切面高度的平面。这三个平面可以定义视图范围的主要范围。如图-1所示。

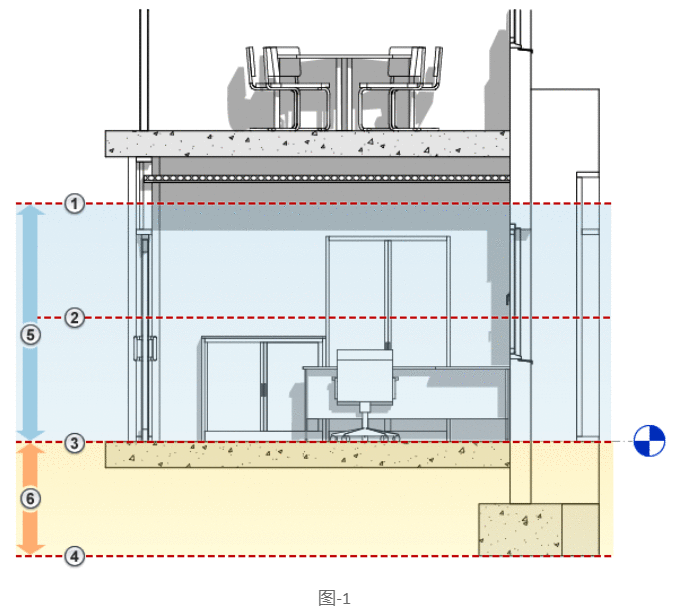
　　①代表顶部②代表剖切面③代表底部④代表偏移⑤代表主要范围⑥视图深度。

　　下面将结合具体的例子详细解释每个功能。

　　首先&＃xff0c;我们绘制了图-2中的构件&＃xff0c;并注意我们在绘制墙体时选择具有截面填充图案的墙体。此时的视图范围如图-2所示。

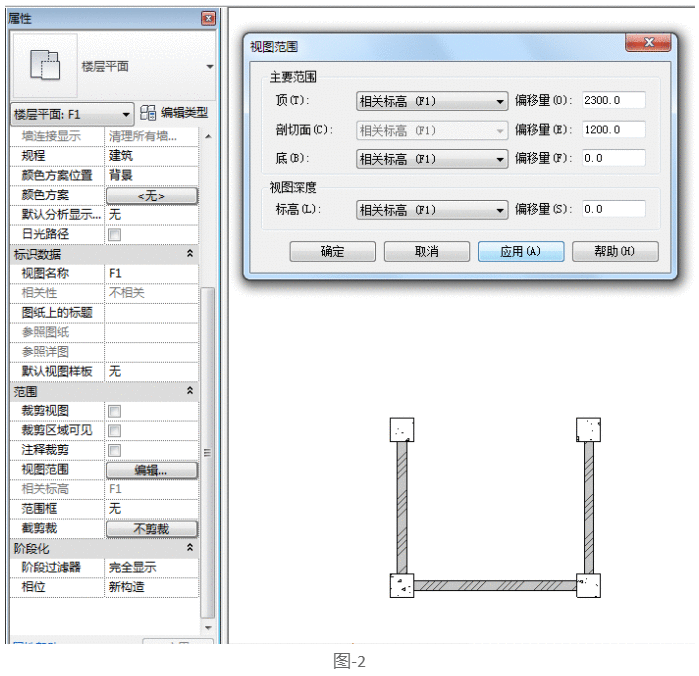
　　绘制完成后&＃xff0c;在项目北部的两根柱子之间绘制一根梁。绘制完成后&＃xff0c;我们会发现我们看不到我们绘制的梁。原因是层高度为3000&＃xff0c;视图的剖切面只能看到高度低于1200的构建。因此&＃xff0c;我们需要将剖切面设置为3000(请注意&＃xff0c;我们还必须将顶部数据设置为3000&＃xff0c;因为系统规定剖切面必须低于顶层平面之下)。完成后&＃xff0c;如图-3所示。

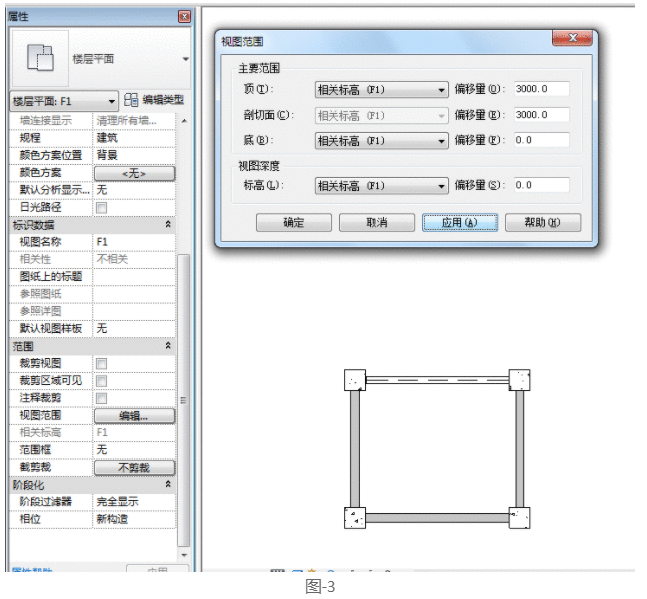
　　我们可以发现一个变化。现在&＃xff0c;由于剖切面的高度是墙的高度&＃xff0c;墙没有被剖切面剖切&＃xff0c;所以我们现在看不到墙的填充图案。

　　现在进入F2视图&＃xff0c;绘制二层构建。如图-4所示&＃xff0c;我们绘制了三面墙。在项目西处&＃xff0c;我们在“属性对话框”中设置了“底部限制条件”&＃xff1a;F2“底部偏移”&＃xff1a;2000、顶部约束&＃xff1a;无连接、无连接高度&＃xff1a;3000。项目东墙设置为“底部限制条件”&＃xff1a;F2、底部偏移&＃xff1a;0“顶部约束”&＃xff1a;无连接、无连接高度&＃xff1a;1000。绘制完成后&＃xff0c;我们将F2属性对话框中的基线设置为无。完成后&＃xff0c;如图所示。

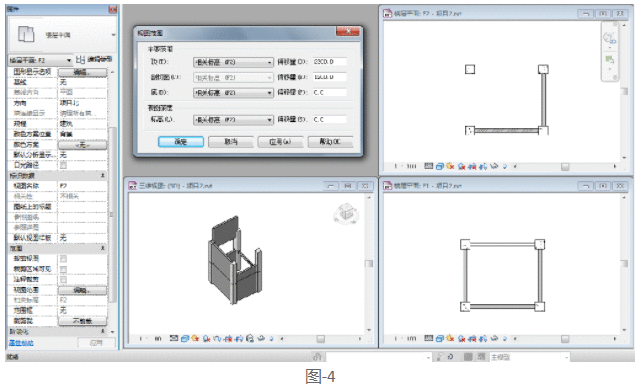
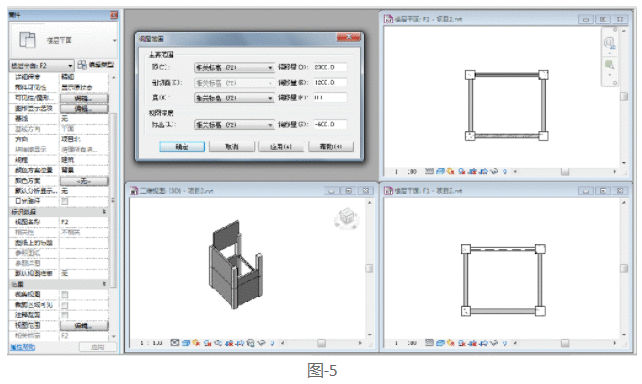
　　此时&＃xff0c;我们将F2中的视图深度设置为-600。在F1视图中&＃xff0c;我们可以看到西侧的墙体和梁。如图-5所示。

　　【推荐】好用的综合bim插件——BIM建模助手

　　BIM建模助手有“视图定位”“快速剖面”“垂直剖面”“水平剖面”“局部三维”“本层三维”等等120&＃43;功能&＃xff0c;共有五个模块全部一起【365圆】&＃xff0c;免费试用一个月。

　　新春活动&＃xff1a;

　　1、虎年大吉&＃xff0c;换壁纸&＃xff0c;赢88.88红包。

　　2、BIM建模助手(共五个模块)买一(年)送二(月)。

　　https://www.zhbim.com/?source&＃61;csdn