HOJ1402：整数分解与组合优化问题研究

HOJ1402 整数划分

http://acm.hit.edu.cn/hoj/problem/view?id&＃61;1402

【题目描述】

整数划分是一个经典的问题。希望这道题会对你的组合数学的解题能力有所帮助。

Input

每组输入是两个整数n和k。(1 <&＃61; n <&＃61; 50, 1 <&＃61; k <&＃61; n)

Output

对于每组输入&＃xff0c;请输出六行。

第一行&＃xff1a; 将n划分成若干正整数之和的划分数。
第二行&＃xff1a; 将n划分成k个正整数之和的划分数。
第三行&＃xff1a; 将n划分成最大数不超过k的划分数。
第四行&＃xff1a; 将n划分成若干奇正整数之和的划分数。
第五行&＃xff1a; 将n划分成若干不同整数之和的划分数。
第六行&＃xff1a; 打印一个空行。

Sample Input

5 2

Sample Output

7
2
3
3
3

Hint:

1. 将5划分成若干正整数之和的划分为&＃xff1a; 5, 4&＃43;1, 3&＃43;2, 3&＃43;1&＃43;1, 2&＃43;2&＃43;1, 2&＃43;1&＃43;1&＃43;1, 1&＃43;1&＃43;1&＃43;1&＃43;1
2. 将5划分成2个正整数之和的划分为&＃xff1a; 3&＃43;2, 4&＃43;1
3. 将5划分成最大数不超过2的划分为&＃xff1a; 1&＃43;1&＃43;1&＃43;1&＃43;1, 1&＃43;1&＃43;1&＃43;2, 1&＃43;2&＃43;2
4. 将5划分成若干奇正整数之和的划分为&＃xff1a; 5, 1&＃43;1&＃43;3, 1&＃43;1&＃43;1&＃43;1&＃43;1
5. 将5划分成若干不同整数之和的划分为&＃xff1a; 5, 1&＃43;4, 2&＃43;3

【算法分析】

本题相当于5个小问题&＃xff0c;首先来看最容易做的第5个小问题&＃xff1a;将n划分成若干不同整数之和的划分数。则是一个典型的背包装物品问题&＃xff0c;把问题转化一下&＃xff0c;即一个容量为n的背包&＃xff0c;重量分别为1到n的物品各一个&＃xff0c;求用若干物品将背包填满的方案总数。

利用动态规划的思想&＃xff0c;很容易得到方程F[I,J] &＃61; F[I-1,J] &＃43;F[I-1,J-I]&＃xff0c;其中F[I,J]表示从前I个物品中用若干个组成的总重量为J的方案总数&＃xff0c;转移时要保证F[I-1,J-I]有意义。答案为F[n,n]&＃xff0c;时间复杂度为O(n²)。

对于前3个小问题可以归结为一个问题&＃xff0c;即第2个小问题&＃xff1a;把将n划分成k个正整数之和的划分数。

为了避免重复&＃xff0c;我们需要按照不下降的顺序进行排列。我们形象地可以把n的k份自然数划分看作n块积木堆成k列&＃xff0c;那么不妨设这n块积木从左到右被堆成“阶梯状”。比如&＃xff0c;下图表示的是3种10的4份自然数划分。

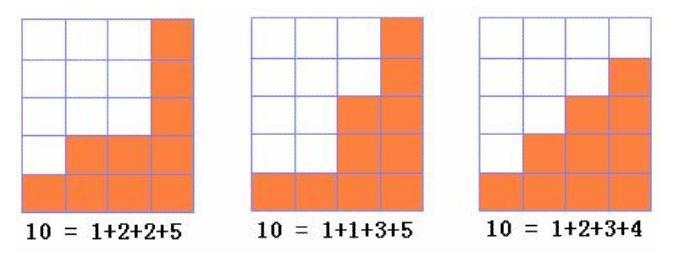
而将该图旋转90度&＃xff0c;可以很容易想出一种状态表示方法。

设F[I,J,K]表示把J划分成I份最大为K的划分方案数&＃xff0c;则有F[I,J,K] &＃61; ∑F[I-1,J-K,L]&＃xff0c;其中L &＃61; 1..K。时间复杂度为O&＃xff08;n²k²&＃xff09;。

而如果观察第一个图&＃xff0c;我们还可以得到一种状态表示方式。设F[I,J]表示把I划分成J份的划分方案数&＃xff0c;则有F[I,J] &＃61; ∑F[I-J,K] &＃xff0c;其中K &＃61; 0..J。时间复杂度为O&＃xff08;nk²&＃xff09;。

又由于F[I,J]&＃61;∑F[I-J,K]&＃xff08;K &＃61; 0..J&＃xff09;&＃61;∑F[I-J,K]&＃xff08;K &＃61; 0..J-1&＃xff09;&＃43;F[I-J,J] &＃61; F[I-1,J-1]&＃43;F[I-J,J]&＃xff0c;这样就把时间复杂度降为O&＃xff08;nk&＃xff09;。从另外一个角度想&＃xff0c;我们在第一个图中“截去底边”&＃xff0c;由于存在一个划分方案中含1的情况&＃xff0c;我们无法确定在“截去底边”之后要把I-J分为几个数&＃xff0c;那么不妨将划分方案中含1的情况单独列出来讨论&＃xff0c;直接得到F[I,J] &＃61; F[I-1,J-1]&＃43;F[I-J,J]。

对于第1个小问题的答案是∑F[N,I]&＃xff08;I &＃61; 1..N&＃xff09;&＃xff0c;第2个小问题的答案显然是F[N,K]&＃xff0c;而第3个小问题的答案则是∑F[N,I]&＃xff08;I &＃61; 1..K&＃xff09;&＃xff0c;考虑上面旋转90度之后的图&＃xff0c;你会发现&＃xff0c;F[N,I]集合中的最高高度均为I&＃xff0c;即将n划分成最大数为I的方案数。

最后来看第4个小问题&＃xff0c;就是第2个小问题的分奇偶版本&＃xff0c;那么设F[I,J]表示把I划分成J个奇数的划分方案数&＃xff0c;G[I,J] 表示把I划分成J个偶数的划分方案数。那么还是用“截去底边”的思想&＃xff0c;显然有G[I,J] &＃61; F[I-J,J]。但F[I,J]却不是直接等于G[I-J,J]&＃xff0c;因为这里又存在一个划分方案中含1的情况&＃xff0c;同样将划分方案中含1的情况单独列出来讨论&＃xff0c;则有F[I,J] &＃61; G[I-J,J] &＃43; F[I-1,J-1]。最后的答案就是∑F[N,I]&＃xff08;I &＃61; 1..N&＃xff09;&＃xff0c;时间复杂度为O(n²)。