作者:广告公司英子 | 来源:互联网 | 2024-11-30 17:55
时间限制:2000/1000 MS (Java/Other) 内存限制:65536/32768 K (Java/Other)
总提交次数:81160 接受的提交次数:29106
问题描述
有一只经过特殊训练的蜜蜂,它只能向前移动到相邻的蜂巢,不能向后移动。给定两个蜂巢位置a和b(0
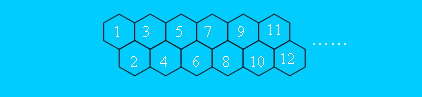
输入
输入的第一行是一个整数N,表示测试案例的数量。接下来的N行,每行包含两个整数a和b(0
输出
对于每个测试案例,输出蜜蜂从蜂巢a移动到蜂巢b的所有可能路径数量,每个结果占一行。
示例输入
示例输出
作者
lcy
来源
递推求解专题练习(适合初学者)
问题链接:HDU2044 蜜蜂的路径选择。这是一道基础训练题,推荐使用C语言解决。
问题简述:参考上述链接。
问题分析:此问题与HDU2041 超级楼梯类似,但有细微差别。考虑蜜蜂位于第n个蜂巢时,它可以从前一个或前两个蜂巢到达当前位置。因此,可以得出递推公式f(n) = f(n-2) + f(n-1),这是一个斐波那契数列的问题。然而,初始条件略有不同:f(1) = 0,f(2) = 1,f(3) = 2,f(n) = f(n-2) + f(n-1) (n > 3)。计算从a到b的路径数量等同于从1到b-a+1的路径数量。为了提高效率,建议预先计算并存储这些值。
程序说明:略。
以下是通过编译的C语言程序:
/* HDU2044 蜜蜂的路径选择 */
#include
#define MAXN 50
typedef unsigned long long ULL;
ULL fn[MAXN+1];
void setfn() {
int i;
fn[0] = 0;
fn[1] = 0;
fn[2] = 1;
fn[3] = 2;
for(i = 4; i <= MAXN; i++)
fn[i] = fn[i-2] + fn[i-1];
}
int main(void) {
int n, a, b;
// 预先计算所有可能的路径数量
setfn();
scanf("%d", &n);
while(n--) {
// 读取起始和目标蜂巢位置
scanf("%d%d", &a, &b);
// 输出结果
printf("%lld\n", fn[b - a + 1]);
}
return 0;
}