关于LeNet5卷积神经网络S2层与C3层连接的参数计算的思考？？？

关于LeNet-5卷积神经网络

S2层与C3层连接的参数计算的思考？？？

首先图1是LeNet-5的整体网络结构图

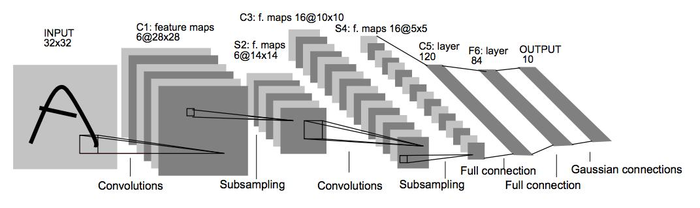
图1 LeNet-5结构

该神经网络共有7层（不计输入层），输入图像大小为32×32。

层编号特点：英文字母+数字

                   英文字母代表以下一种：

                   C→卷积层、S→下采样层（池化）、F→全连接层

                   数字代表当前是第几层，而非第几卷积层（池化层.ec）

术语解释：参数→权重w与偏置b

                连接数→连线数

参数计算：每个卷积核对应于一个偏置b，卷积核的大小对应于权重w的个数(特别注意通道数)

C1层：使用6个5×5大小的卷积核，padding=0，stride=1进行卷积，得到6个28×28大小的特征图（32-5+2*0）/1+1=28

  参数个数：（5*5+1）*6=156，其中5*5为卷积核的25个参数，1为偏置

  连接数： 156*28*28=122304，其中156为卷积过程连线数，28*28为输出特征层每一个像素都由前面卷积得到

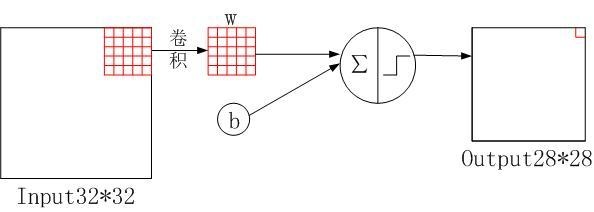
S2层：使用2×2大小的卷积核进行池化，padding=0，stride=2，得到6个14×14大小的特征图（28-2+2*0）/2+1=14

  参数个数：（1+1）*6=12，其中第一个1为最大池化所对应的2*2感受野中最大的那个数的权重，第二个1为偏置

  连接数： （2*2+1）*14*14*6= 5880，虽然只选取2*2感受野中最大的那个数，但也存在2*2的连接数，即最大的权重为1，其余的为0

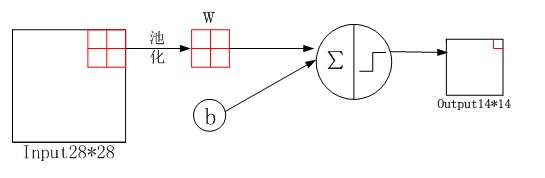
C3层：该层使用16个5*5大小的卷积核，padding=0，stride=1，卷积后得到16个10*10的特征图，（14-5+2*0）/1+1=10

该层第一个难点：6个输入图如何通过卷积得到16个特征图？

如图2所示，C3的前六个特征图(0,1,2,3,4,5)由S2的相邻三个特征图作为输入，接下来的6个特征图(6,7,8,9,10,11)由S2的相邻四个特征图作为输入，12,13,14号特征图由S2间断的四个特征图作为输入，15号特征图由S2全部(6个)特征图作为输入。

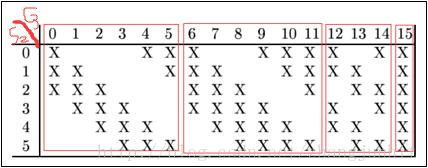
图2

该层第二个难点(这里我觉得最难理解，断断续续理解了几乎小半年)：通过S2的输入，如何卷积得到C3的一个特征图呢？

我用C3层0号特征图举例，它由S2层0,1,2号特征图作为输入，由于C3层共有16个卷积核，即C3每一个特征图是由一个卷积核对S2层相应的输入特征图卷积得到的，如图3所示。

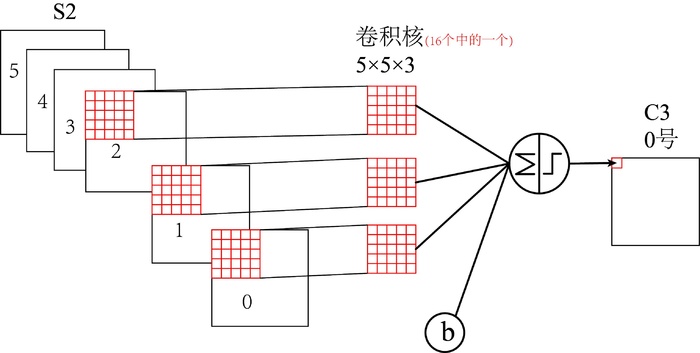
图3

这里值得注意的是，上图的卷积核是一个5×5大小具有3个通道，每个通道各不相同，这也是下面计算时5*5后面还要乘以3,4,6的原因。具体可参考多通道卷积。

参数个数：（5*5*3+1）*6+（5*5*3+1）*6+（5*5*4+1）*3+（5*5*6+1）=1516

连接数：1516*10*10=151600

S4层：依然是池化层，使用16个2×2大小的卷积核进行池化，padding=0，stride=2，得到16个5×5大小的特征图（10-2+2*0）/2+1=5

  参数个数：（1+1）*16=32

       连接数：  （2*2+1）*16*5*5=2000

C5层：使用120个5*5卷积核对S4层16个特征图进行卷积，padding=0，stride=1，得到120个1*1大小的特征图，（5-5+2*0）/1+1=1

这里的计算跟C3相同，也是多通道卷积，因此5*5后面乘以16.

  参数个数：（5*5*16+1）*120=48120

       连接数：  （5*5*16+1）*120*1*1=48120

F6层：共有84个神经元，与C5层进行全连接，即每个神经元都与C5层的120个特征图相连。

   参数个数：（120+1）*84=10164

       连接数：  （120+1）*84=10164

Output层：输出层由欧式径向基函数（Euclidean Radial Basis Function）单元组成，每个单元由F6层84个神经元作为输入，输出0-9十个手写数字识别的结果

   参数个数：84*10=840

       连接数：  84*10=840

总结：本人初学深度学习，尚有太多不懂的地方，上述若有错误的地方，望请各位批评指正。在学习lenet-5的过程中，发现了一个可视化的网站：http://scs.ryerson.ca/~aharley/vis/conv/flat.html

http://scs.ryerson.ca/~aharley/vis/conv/

如果打不开，请多换几个浏览器

多通道卷积：可以看出卷积核W0，W1各自的三个通道各不相同

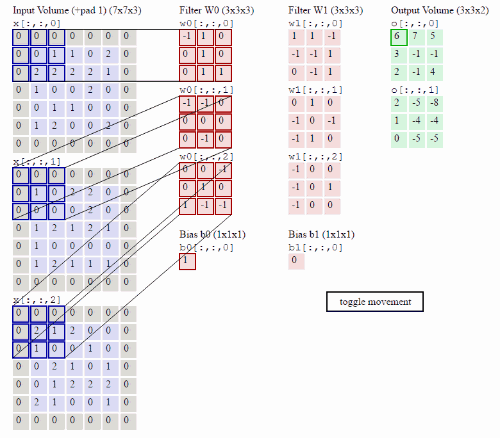
最后，引用了几个参考文章的链接：

http://blog.csdn.net/zhangjunhit/article/details/53536915

https://www.jianshu.com/p/ce609f9b5910

http://blog.csdn.net/qiaofangjie/article/details/16826849

https://www.zybuluo.com/hanbingtao/note/485480