关于如下2个矩阵为何是相似矩阵?

假设有1个线性变换,如下所示,它可以将任意向量(x,y)映射为关于45°直线的镜像(y,x):

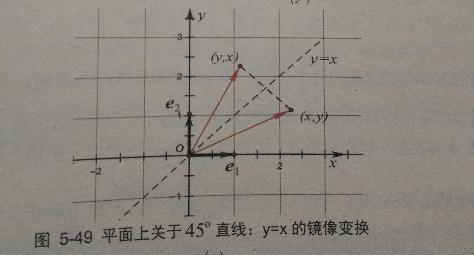
我们可以很容易的求出其变换矩阵A为$$\begin{bmatrix}0 & 1 \\ 1& 0 \\\end{bmatrix}$$。
现在我们使用新的基底,使得新的基向量e1'沿着45°直线,即e1'=(1,1),而另1个基向量e2'=(-1,1)。如下所示:

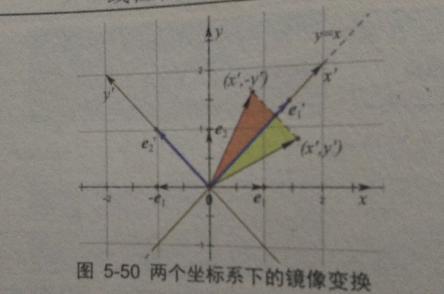
而其变换矩阵B为$$\begin{bmatrix}1 & 0 \\ 0 & -1 \\ \end{bmatrix}$$。
现在想知道这个变换矩阵B是怎样求解出来的?