高斯同余理论_高斯模糊算法

1、鲸群优化算法

请参考这里。

2、改进鲸群优化算法

（1）高斯差分变异策略

利用当前最优鲸的位置、当前鲸的位置与鲸群中随机个体进行高斯差分，由于高斯差分变异可以在当前变异个体附近生成更大的扰动，使得算法更容易跳出局部极值，其数学表达式如下： X ( t + 1 ) = p 1 ⋅ f 1 ⋅ ( X ∗ − X ( t ) ) + p 2 ⋅ f 2 ⋅ ( X r a n d − X ( t ) ) (1) \boldsymbol X(t+1)=p_1\cdot f_1\cdot(\boldsymbol X^*-\boldsymbol X(t))+p_2\cdot f_2\cdot(\boldsymbol X_{rand}-\boldsymbol X(t))\tag{1} X(t+1)=p1​⋅f1​⋅(X∗−X(t))+p2​⋅f2​⋅(Xrand​−X(t))(1)其中， p 1 p_1 p1​和 p 2 p_2 p2​为权重系数，取值均为0.5； f 1 f_1 f1​和 f 2 f_2 f2​是以产生均值为0、方差为1的高斯分布随机数函数作为高斯分布函数系数； X ∗ \boldsymbol X^* X∗为当前最优个体位置； X r a n d \boldsymbol X_{rand} Xrand​为随机选择鲸的位置向量；$\mathbf{X}(t)$为当前鲸的个体位置。
在算法迭代过程中根据式(1)对鲸群个体进行扰动，算法迭代前期，由于种群分布不均，所以个体位置分布差距较大，因此算法主要通过差分变量对个体进行扰动，从而产生多样性个体，使算法能够快速收敛；随着算法迭代的不断进行，鲸群大多数个体位置不会发生太大变化，此时算法主要通过高斯分布函数系数对种群进行扰动，从而帮助算法降低陷入局部最优
的可能性，避免发生早熟。将引入高斯差分变异策略的鲸群算法命名为GWOA。

（2）对数惯性权重策略

对数惯性权重策略如下： w = ( t / M a x _ i t e r ) × ( lg ⁡ w m a x / lg ⁡ w m i n ) − lg ⁡ w m a x (2) w=(t/Max\_iter)×(\lg w_{max}/\lg w_{min})-\lg w_{max}\tag{2} w=(t/Max_iter)×(lgwmax​/lgwmin​)−lgwmax​(2)其中，$t$为当前迭代次数；$Max\_iter$为最大迭代次数； w m a x w_{max} wmax​表示惯性权重最大值， w m i n w_{min} wmin​表示惯性权重最小值。权重将随着迭代次数增加而增加。新的位置更新公式如下： X ( t + 1 ) = w ⋅ X ∗ − A ⋅ D (3) \boldsymbol X(t+1)=w\cdot\boldsymbol X^*-\boldsymbol{A\cdot D}\tag{3} X(t+1)=w⋅X∗−A⋅D(3)所以，本文采用对数惯性权重策略，迭代前期，惯性权重提高鲸群全局搜索能力，使鲸群个体能够更快地搜寻到最优猎物；迭代后期，通过惯性权重线性增长策略，使惯性权重增大，从而使算法在后期局部开发过程中更易跳出局部极值，从而寻找到最优值。将引入对数惯性权重和高斯差分变异策略的鲸群算法命名为IGWOA。

（3）IGWOA算法步骤

对原始WOA进行高斯差分变异与对数惯性权重两方面改进，得到的IGWOA的算法伪代码，如下所示：

IGWOA与WOA和GWOA对24个测试函数进行算法比较，与WOA和GWOA进行比较，各算法的参数设置为：种群规模均设置为30， p 1 = 0.5 , p 2 = 0.5 , w m a x = 0.9 , w m i n = 0.4 , M a x _ i t e r = 500 p_1=0.5,p_2=0.5,w_{max}=0.9,w_{min}=0.4,Max\_iter=500 p1​=0.5,p2​=0.5,wmax​=0.9,wmin​=0.4,Max_iter=500，3种算法对每个函数独立运行30次，记录它们的最大值、最小值、平均值与标准差。以F1~F3为例。
下图为对F1的测试寻优曲线。
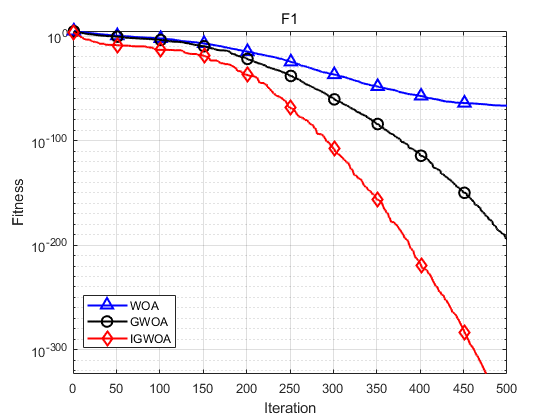最大值、最小值、平均值与标准差显示如下：

函数：F1
WOA：最大值: 7.8859e-66,最小值:6.4042e-86,平均值:2.6287e-67,标准差:1.4398e-66
GWOA：最大值: 2.2057e-193,最小值:4.1476e-219,平均值:7.3525e-195,标准差:0
IGWOA：最大值: 0,最小值:0,平均值:0,标准差:0


下图为对F2的测试寻优曲线。
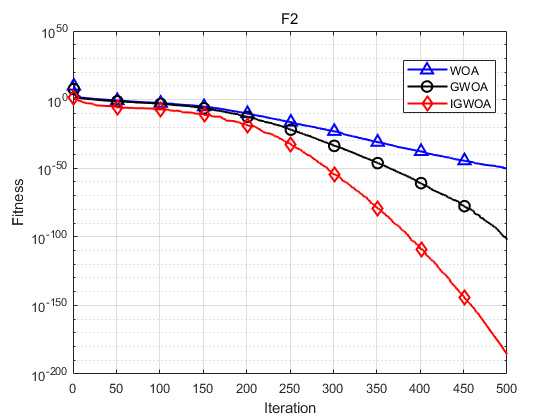最大值、最小值、平均值与标准差显示如下：

函数：F2
WOA：最大值: 1.5564e-49,最小值:4.3065e-58,平均值:8.7126e-51,标准差:2.9127e-50
GWOA：最大值: 1.1184e-101,最小值:4.7713e-110,平均值:6.4373e-103,标准差:2.1564e-102
IGWOA：最大值: 6.9392e-185,最小值:3.5595e-198,平均值:3.1056e-186,标准差:0


下图为对F3的测试寻优曲线。
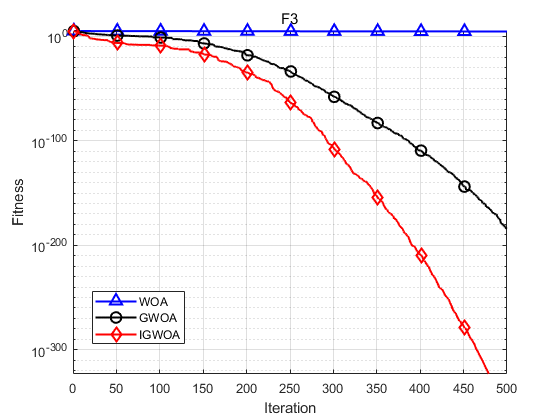最大值、最小值、平均值与标准差显示如下：

函数：F3
WOA：最大值: 60074.57,最小值:44313.3563,平均值:50857.0743,标准差:3582.8828
GWOA：最大值: 1.5995e-183,最小值:1.3018e-221,平均值:5.3318e-185,标准差:0
IGWOA：最大值: 0,最小值:0,平均值:0,标准差:0


综上，IGWOA在收敛精度、收敛速度、个体多样性以及鲁棒性方面与其他改进群智能优化算法相比具有优势。

[1] 陈雷, 尹钧圣. 高斯差分变异和对数惯性权重优化的鲸群算法[J]. 计算机工程与应用, 2021, 57(2): 77-90.