原文地址

拉普拉斯矩阵

Laplacian matrix 的定义

谈到机器学习中的降维技术&＃xff0c;可能大多数了解一点机器学习的朋友都知道PCA&＃xff0c;今天为大家介绍一种新的降维方法——拉普拉斯特征映射

拉普拉斯矩阵&＃xff08;Laplacian matrix)&＃xff09;&＃xff0c;也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图G&＃61;&＃xff08;V&＃xff0c;E&＃xff09; &＃xff0c;其拉普拉斯矩阵被定义为:L&＃61;D-W

其中D为图的度矩阵&＃xff0c;W为图的邻接矩阵。&＃xff08;不知道度矩阵和邻接矩阵的请自行百度&＃xff09;

拉普拉斯矩阵L的性质

• L是对称半正定矩阵&＃xff1b;
• L 1 &＃61; 0 1 &＃xff0c;即 的最小特征值是0&＃xff0c;相应的特征向量是 。证明&＃xff1a;L* 1 &＃61; ( D-W) * 1 &＃61; 0 &＃61; 0 * 1 。
• L 有n个非负实特征值
• 且对于任何一个属于实向量f &＃xff0c;有以下式子成立 : 
  

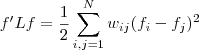
证明如下&＃xff1a; 

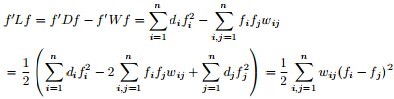
Laplacian Eigenmaps 拉普拉斯特征映射

Laplacian Eigenmaps 是用局部的角度去构建数据之间的关系。如果两个数据实例i和j很相似&＃xff0c;那么i和j在降维后目标子空间中应该尽量接近。它的直观思想是希望相互间有关系的点&＃xff08;在图中相连的点&＃xff09;在降维后的空间中尽可能的靠近。Laplacian Eigenmaps可以反映出数据内在的流形结构。 

使用时算法具体步骤为&＃xff1a;

步骤1&＃xff1a;构建图

使用某一种方法来将所有的点构建成一个图&＃xff0c;例如使用KNN算法&＃xff0c;将每个点最近的K个点连上边。K是一个预先设定的值。这样构建的图矩阵就是一个稀疏矩阵&＃xff0c;只保留了最相似的K个邻居关系。

步骤2&＃xff1a;确定权重

确定点与点之间的权重大小&＃xff0c;例如选用热核函数来确定&＃xff08;当然这个地方你完全可以选择其他的相似度度量方式来衡量&＃xff09;&＃xff0c;如果点i和点j相连&＃xff0c;那么它们关系的权重设定为&＃xff1a;

使用最小的m个非零特征值对应的特征向量作为降维后的结果输出。

前面提到过&＃xff0c;Laplacian Eigenmap具有区分数据点的特性&＃xff0c;可以从下面的例子看出&＃xff1a; 

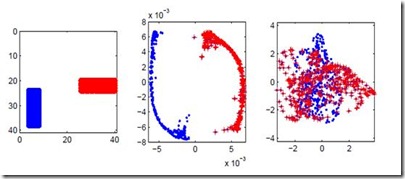
见图1所示&＃xff0c;左边的图表示有两类数据点&＃xff08;数据是图片&＃xff09;&＃xff0c;中间图表示采用Laplacian Eigenmap降维后每个数据点在二维空间中的位置&＃xff0c;右边的图表示采用PCA并取前两个主要方向投影后的结果&＃xff0c;可以清楚地看到&＃xff0c;在此分类问题上&＃xff0c;Laplacian Eigenmap的结果明显优于PCA。