CNN与FCN
通常cnn网络在卷积之后会接上若干个全连接层,将卷积层产生的特征图(feature map)映射成为一个固定长度的特征向量。一般的CNN结构适用于图像级别的分类和回归任务,因为它们最后都期望得到输入图像的分类的概率,如ALexNet网络最后输出一个1000维的向量表示输入图像属于每一类的概率。
FCN对图像进行像素级的分类,从而解决了语义级别的图像分割问题。与经典的CNN在卷积层使用全连接层得到固定长度的特征向量进行分类不同,FCN可以接受任意尺寸的输入图像,采用反卷积层对最后一个卷基层的特征图(feature map)进行上采样,使它恢复到输入图像相同的尺寸,从而可以对每一个像素都产生一个预测,同时保留了原始输入图像中的空间信息,最后奇偶在上采样的特征图进行像素的分类。
-全卷积网络(FCN)是从抽象的特征中恢复出每个像素所属的类别。即从图像级别的分类进一步延伸到像素级别的分类。
FCN将传统CNN中的全连接层转化成一个个的卷积层。如下图所示,在传统的CNN结构中,前5层是卷积层,第6层和第7层分别是一个长度为4096的一维向量,第8层是长度为1000的一维向量,分别对应1000个类别的概率。FCN将这3层表示为卷积层,卷积核的大小(通道数,宽,高)分别为(4096,1,1)、(4096,1,1)、(1000,1,1)。所有的层都是卷积层,故称为全卷积网络。
FCN特点
1.将普通的分类网络丢弃全连接层,换上对应的卷积层
2.上采样,方法是双线性上采样差,此处的上采样即是反卷积。
3.跳跃结构:因为如果将全卷积之后的结果直接上采样得到的结果是很粗糙的,所以作者将不同池化层的结果进行上采样之后来优化输出,现在我们有1/32尺寸的heatMap,1/16尺寸的featureMap和1/8尺寸的featureMap,如果直接对1/32尺寸的heatMap进行upsampling操作,因为还原的图片仅仅是conv5中的卷积核中的特征,限于精度问题不能够很好地还原图像当中的特征,因此
把conv4中的卷积核对上一次upsampling之后的图进行反卷积补充细节(相当于一个差值过程),最后把conv3中的卷积核对刚才upsampling之后的图像进行再次反卷积补充细节,最后就完成了整个图像的还原。
网络结构
网络结构如下。输入可为任意尺寸图像彩色图像;输出与输入尺寸相同,深度为:20类目标+背景=21。 (在PASCAL数据集上进行的,PASCAL一共20类)
作者的FCN主要使用了三种技术:
- 不含全连接层(fc)的全卷积(fully conv)网络。可适应任意尺寸输入。
- 增大数据尺寸的反卷积(deconv)层。能够输出精细的结果。
- 结合不同深度层结果的跳级(skip)结构。同时确保鲁棒性和精确性。

16*16*21变成34*34*21:参考:https://blog.csdn.net/py184473894/article/details/83748891讲解了完整caffe文件结构。
对于deconvolution: output = (input - 1) * stride + ksize - 2 * padding;
layer {name: "upscore2"type: "Deconvolution"bottom: "score_fr"top: "upscore2"param {lr_mult: 0}convolution_param {num_output: 21bias_term: falsekernel_size: 4stride: 2}
}
upscore2:输入为16*16*21 输入为34*34*21
crop
注意:为了得到和输入图像尺寸完全相同的特征图,FCN中还使用了crop操作来辅助反卷积操作,因为反卷积操作并不是将特征图恰好放大整数倍。图中灰色区域。
layer {name: "crop_layer"type: "Crop"bottom: "A"bottom: "B"top: "C"crop_param {axis: 1offset: 25offset: 128offset: 128}
}
偏移参数用于告诉裁剪层准确裁剪的位置
Crop_layer的主要作用就是进行剪裁。Caffe中的数据是以 blobs形式存在的,blob是四维数据,即Blob是4D :(批量大小,通道数/过滤器数,高度,宽度)=(N,C,H,W)
1-crop bottom A is (20, 50, 512, 512)
2-reference bottom B is (20, 10, 256, 256)
3-the top blob C (result blob) will be (20, 10, 256, 256)
在这个例子中,我们想要裁剪尺寸1,2和3.但是保持尺寸0固定。所以我们设置axis= 1(将裁剪1和所有后续轴)
另一个参数'offset'指定裁剪在A中的确切位置。显然,此参数没有默认值,必须指定。
指定3个偏移:比如偏移=(25,128,128)所以轴= 1,偏移=(25,128,128)
numpy语法中的裁剪操作将是:C = A [:,25:25 + B.shape [1],128:128 + B.shape [2],128:128 + B.shape [3]]
用语言来说:这只会采用A 25到35的过滤器而忽略其余部分。 并为空间维度做中心裁剪
from :https://blog.csdn.net/sunshine_in_moon/article/details/52900338
全卷积层:
假设卷积神经网络的输入是224x224x3的图像,一系列的卷积层和下采样层将图像数据变为尺寸为 7x7x512 的数据体。AlexNet使用了两个尺寸为4096的全连接层,最后一个有1000个神经元的全连接层用于计算分类评分。我们可以将这3个全连接层中的任意一个转化为卷积层:
第一个连接区域是[7x7x512]的全连接层,令其滤波器尺寸为Kernel=7,这样输出数据体就为[1x1x4096]了;
第二个全连接层,令其滤波器尺寸为Kernel=1,这样输出数据体为[1x1x4096];
最后一个全连接层也做类似的,令其Kernel=1,最终输出为[1x1x1000]。
转化的意义
这样的变换每次都需要把全连接层的权重W重塑成卷积层的滤波器。如果想让卷积网络在一张更大的输入图片上滑动,得到多个输出,那么卷积层可以在单次前向传播中完成全连接层几次才能完成的操作。
假设想让224×224的滑窗,以32的步长在384×384的图片上滑动,将每个位置的特征都提取到网络中,最后得到6×6个位置的类别得分。如果224×224的输入图片经过卷积层和下采样层之后得到了[7x7x512]的特征图,那么,384×384的大图片直接经过同样的卷积层和下采样层之后会得到[12x12x512]的特征。然后再经过上面由3个全连接层转化得到的3个卷积层,最终得到[6x6x1000]的输出((12 – 7)/1 + 1 = 6)。这个结果正是滑窗在原图中6×6个位置的得分。
对于384×384的图像,让(含全连接层)的初始卷积神经网络以32像素的步长独立对图像中的224×224块进行多次评价,其效果和使用把全连接层变换为卷积层后的卷积神经网络进行一次前向传播是一样的。所以将全连接层转换成卷积层会更简便。
CNN中输入的图像大小是固定resize成 227x227 大小的图像,第一层pooling后为55x55,第二层pooling后图像大小为27x27,第五层pooling后的图像大小为13*13。
而FCN输入的图像是H*W大小,第一层pooling后变为原图大小的1/4,第二层变为原图大小的1/8,第五层变为原图大小的1/16,第八层变为原图大小的1/32。经过多次卷积和pooling以后,得到的图像越来越小,分辨率越来越低。其中图像到 H/32,W/32 的时候图片是最小的一层时,所产生图叫做heatmap,是我们最重要的高维特征图,得到高维特征的heatmap之后就是最重要的一步也是最后的一步对原图像进行upsampling,把图像进行放大、放大、放大到原图像的大小。
我的理解:放大的尺寸根据缩放的比例来求,通过参数步长stride来确定,对于反卷积来说,stride=n,相当于先对featuremap每个像素间隔插入n个“0”元素,然后使用卷积核进行计算。???
反卷积-升采样
卷积操作如下:
通过滑动卷积核,就可以得到整张图片的卷积结果,

full卷积:
下图表示的是参数为( i′=2,k′=3,s′=1,p′=2)的反卷积操作,其对应的卷积操作参数为 (i=4,k=3,s=1,p=0)。我们可以发现对应的卷积和非卷积操作其 (k=k′,s=s′),但是反卷积却多了p′=2。通过对比我们可以发现卷积层中左上角的输入只对左上角的输出有贡献,所以反卷积层会出现 p′=k−p−1=2。通过示意图,我们可以发现,反卷积层的输入输出在 s=s′=1 的情况下关系为:
o′=i′−k′+2p′+1=i′+(k−1)−2p
 (为什么padding加的越多,最后输出越小)。下图是当stride=2时的反卷积情况:
(为什么padding加的越多,最后输出越小)。下图是当stride=2时的反卷积情况:

卷积: 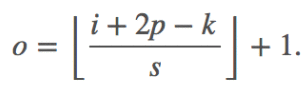
反卷积: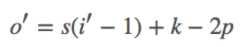 ,可以把式中的p=k-1-p′
,可以把式中的p=k-1-p′
假设原图是3X3,首先使用上采样让图像变成7X7,可以看到图像多了很多空白的像素点。使用一个3X3的卷积核对图像进行滑动步长为1的valid卷积,得到一个5X5的图像,我们知道的是使用上采样扩大图片,使用反卷积填充图像内容,使得图像内容变得丰富,这也是CNN输出end to end结果的一种方法。
下半部分,反卷积层(橙色×3)可以把输入数据尺寸放大。和卷积层一样,上采样的具体参数经过训练确定。
这里图像的反卷积与下图的full卷积原理是一样的,使用了这一种反卷积手段使得图像可以变大,FCN作者使用的方法是这里所说反卷积的一种变体,这样就可以获得相应的像素值,图像可以实现end to end。
(feature map值与权重不同,生成的上采样的二值区域也是不一样的。)


使用上采样操作;并且将这些特征图进行上采样之后,将特征图对应元素相加,FCN为了得到信息,使用上采样(使用反卷积)实现尺寸还原。不仅对pool5之后的特征图进行了还原,也对pool4和pool3之后的特征图进行了还原,结果表明,从这些特征图能很好的获得关于图片的语义信息,而且随着特征图越来越大,效果越来越好。
逐像素点预测分类
采用反卷积层对最后一个卷积层的feature map进行上采样, 使它恢复到输入图像相同的尺寸,从而可以对每个像素都产生了一个预测, 同时保留了原始输入图像中的空间信息, 最后在上采样的特征图上进行逐像素分类。
具体过程:经过多次卷积和pooling以后,得到的图像越来越小,分辨率越来越低。

from:https://blog.csdn.net/qq_36269513/article/details/80420363
from:https://www.cnblogs.com/ywheunji/p/10154757.html
原文:https://people.eecs.berkeley.edu/~jonlong/long_shelhamer_fcn.pdf