EducationalCodeforcesRound104(RatedforDiv.2)B.CatCycle

原题链接https://codeforces.com/contest/1487/problem/B

题目大意：有段长度和AB两只猫。A猫从点出发每次向前走一步，到达1之后重新回到n点（即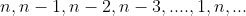：)，B猫从点出发，每次向后走一步，到达n之后回到1点（即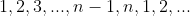：)但是A猫比B猫强壮，因此AB相遇时B会多向前走一步。问进行k此之后B猫的位置。

解题思路：

1、先想模拟，每次进行一次操作，但是给的数据的最坏时间是1e9 * 1e4，显然会超时。

2、发现n为偶数时，AB不可能会相遇，因为A的位置为奇数时B的位置必为偶数，反之也是。

3、每次相遇的步长为n/2，即每进行n/2次操作只有AB会相遇一次。

4、n为偶数时，B的位置为（k - 1）% n + 1；n为奇数时，B的位置为(k - 1 ) + (k - 1) / (n / 2)) % n + 1。

PS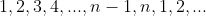：初始位置是从1开始的，要进行k - 1在对结果 + 1的操作，不然的话是从0开始递增。

AC代码：

#include
using namespace std;
#define ll long long
#define MP make_pair
#define SZ(X) ((int)(X).size())
typedef pair PII;
const int INF = 0x3f3f3f3f;
const int N = 1e6 + 10;
int main(){
int T,n,k;
scanf("%d",&T);
while(T --){
scanf("%d%d",&n,&k);
if(n % 2 == 0) printf("%d\n",(k - 1) % n + 1);
else printf("%d\n",((k - 1 ) + (k - 1) / (n / 2)) % n + 1);
}
return 0;
}

刚开始做的时候题目看错了，卡了半天QAQ。