ECC算法简析，椭圆曲线密码，应用于国密SM2

SM2是国密算法的一部分，于2010年由国密局公布，属于非对称加密算法，本身是基于ECC椭圆曲线算法来实现的。

本文重在理清ECC算法的来龙去脉，关于无穷远点、摄影平面坐标系、Fp有限域、阿贝尔群等概念，要重点学习近世代数；关于代码实现部分，本文暂未说明。

一、射影平面的引入

近世代数中的几个小概念：

1关于无穷远点，可以理解为平面上两条平行线的交点；

2一组平行直线只有一个无穷远点；

3相交的两条平行直线有不同的无穷远点（易反正）；

4平面上全体无穷远点构成一条无穷远直线；

5全体平常点和全体无穷远点构成射影平面。

射影平面坐标系是对笛卡尔平面直角坐标系的扩展，能表示无穷远点，同时向下兼容笛

卡尔平面直角坐标系中的平常点。

对于笛卡尔直角坐标系中的平常点A(x,y)，令x=X/Z,y=Y/Z，Z!=0，则点A在射影平面坐标系中表示为A(X,Y,Z)，Z!=0。

直线在笛卡尔平面直角坐标系中的方程为ax+by+c=0，带入x=X/Z,y=Y/Z，得出射影平面坐标系中表示为aX+bY+cZ=0。

然后由两直线aX+bY+c1Z=0，aX+bY+c2Z=0，c1!=c2，易得出Z=0，即aX+bY=0，所以无穷远点在射影平面中用(X,Y,0)来表示。

综上，射影平面坐标系中包括两类点，一类是平常点(X,Y,Z),Z!=0，另一类是无穷远点(X,Y,0)。

二、椭圆曲线的定义

射影平面坐标系上满足威尔斯特拉斯方程（Weierstrass）所有点的集合

Y2Z+a1XYZ+a3YZ2=X3+a2X2Z+a4XZ2+a6Z3Y2Z+a1XYZ+a3YZ2=X3+a2X2Z+a4XZ2+a6Z3，组成一条椭圆曲线。

    并满足：

1椭圆曲线方程是一个齐次方程，所有项的次数都是三。

2曲线上的每个点都必须是非奇异的（光滑的），偏导数FX(X,Y,Z)、FY(X,Y,Z)、FZ(X,Y,Z)不同为0，即曲线上所有点都可微。

椭圆曲线的形状，并不是椭圆形。该方程与椭圆方程的相差甚远，因为椭圆方程是二次的。该曲线之所以命名为椭圆曲线，是因为上述方程类似于计算椭圆周长的方程。

        将x=X/Y,y=Y/Z带入后，得到椭圆曲线方程的所有平常点在笛卡尔坐标系中的表示：

y^2+a1xy+a3y=x^3+a2x^2+a4x+a6

        平常点(x,y)的斜率k=-Fx(x,y)/Fy(x,y)=(3x^2+2a2x+a4-a1y)/(2y+a1x+a3);

三、应用于加密

并不是所有的椭圆曲线都光滑和连续，例如Y^2Z=X^3+X^2和Y^2Z=X^3，在点(0,0,1)上不可微，没有切线。

并不是所有光滑的椭圆曲线都适合加密，y^2=x^3+ax+b是一种简单常用的适合用来加密的椭圆曲线。

另外，我们所说的椭圆曲线上的点包括两部分，一部分(x,y)满足y^2=x^3+ax+b，只是笛卡尔平面直角坐标系中的平常点，还要再加一个无穷远点，才是一条完整的椭圆曲线。

再者，上面所说的(x,y)是定义在R上的，若要用来加密，还需把椭圆曲线离散化，即定义在有限域Fp上面，还要建立起(x,y)之间关系，这个关系是加法运算。

四、有限域Fp

椭圆曲线是连续的，并不适合用于加密；所以，我们必须把椭圆曲线变成离散的点，我

们要把椭圆曲线定义在有限域上。

        下面，我们给出一个有限域Fp，这个域只有有限个元素。
   
　　Fp中只有p（p为素数）个元素0,1,2 …… p-2,p-1；
　　Fp 的加法（a+b）法则是 a+b≡c (mod p)；

　　Fp 的乘法(a×b)法则是  a×b≡c (mod p)；
　　Fp 的除法(a÷b)法则是  a/b≡c (mod p)；即 a×b-1≡c  (mod p)；b-1也是一个0到p-1之间的整数，但满足b×b-1≡1 (mod p)

        Fp 的单位元是1，零元是 0。

       对于椭圆曲线Ep(a,b)，p为质数，x,y∈[0,p-1]。选择两个小于p的非负整数a、b，满足4a3+27b2≠0(mod p)

符合方程y^2=x^3+ax+b(mod p)，满足上述方程的所有点(x,y)，再加上无穷远点，构成一条椭圆曲线。

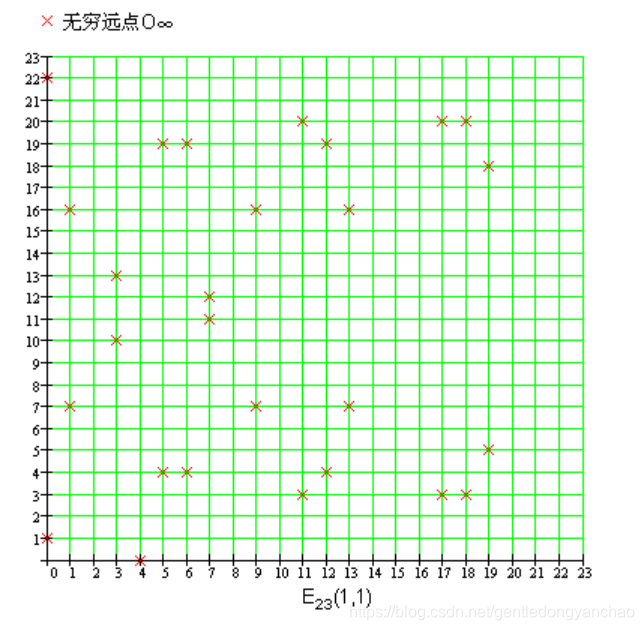
以y^2=x^3+x+1为例，记为E23(1,1)，该椭圆曲线上的离散点为

四、椭圆曲线上点(x,y)的加法运算

我们最熟悉的加法是实数轴上的加法，3+4=7，1.2+68=69.2，2pi+3pi=5pi。

若要实现椭圆曲线上的加法，需要引入近世代数中的阿贝尔群。

阿贝尔群是一种代数结构，由一个集合和二元运算组成，需要满足封闭性、结合性、有单位元和逆元。

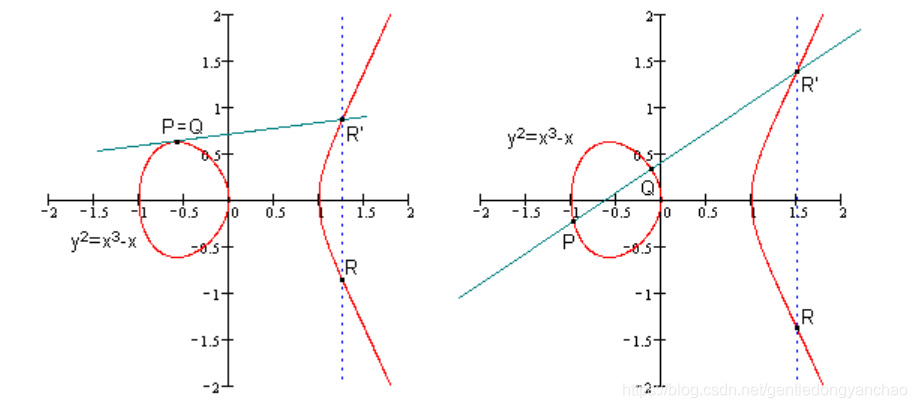
运算法则：任意取椭圆曲线上两点P、Q （若P、Q两点重合，则做P点的切线）做直线交于椭圆曲线的另一点R’，过R’做y轴的平行线交于R。我们规定P+Q=R。

在加密中，加法运算主要使用P+P+…+P(m个相加)=2P+P+…+P=(m-1)P+P=mP。即m个相

同的点P相加。

以P+P+P=2P+P=3P为例，

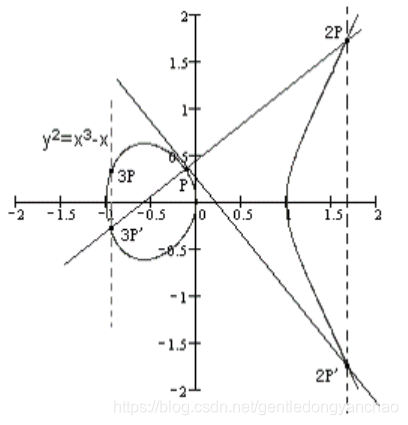
计算过程不断的重复做切线或连接两点，然后再沿着y轴做平行线，取交点的过程。先

有P，做P的切线，然后有2P’，再有2P，再连接2P和P，有3P’，然后再有3P。

五、应用于加密后的椭圆曲线

1椭圆曲线Ep(a,b)上的点的数目，称为椭圆曲线Ep(a,b)的阶。

2对于椭圆曲线上一点P，如果存在最小的正整数n，使得数乘nP=O∞，则将n称为P的阶，若n不存在，我们说P是无限阶的。事实上，在有限域上定义的椭圆曲线上所有的点的阶n都是存在的，具体证明详见近世代数相关理论。

3对于kG=K，点G是Ep(a,b)上的点，由加法定义，求点K相对容易，并且K也在Ep(a,b)上。但是由K和G，去反推k非常困难，被称为椭圆曲线上离散对数难题。

4描述一个利用椭圆曲线进行加密通信的过程：

(1)用户A选定一条椭圆曲线Ep(a,b)，并取椭圆曲线上一点，作为基点G。
　　(2)用户A选择一个私有密钥k，并生成公开密钥K=kG。
　　(3)用户A将Ep(a,b)和点K，G传给用户B。
　　(4)用户B接到信息后 ，将待传输的明文编码到Ep(a,b)上一点M（编码方法很多，这里不作讨论），并产生一个随机整数r。
　　(5)用户B计算点C1=M+rK；C2=rG。
　　(6)用户B将C1、C2传给用户A。
　　(7)用户A接到信息后，计算C1-kC2，结果就是点M。
        因为C1-kC2=M+rK-k(rG)=M+rK-r(kG)=M，再对点M进行解码就可以得到明文。

在这个加密通信中，用户A的加密用的椭圆曲线、公钥和基点，即Ep(a,b)、K、G，用户B的两个返回值C1、C2，会在网络中传输，有可能被盗取，但是通过K、G 求k和通过C2、G求r，都是相对困难的。没有k或r，就无法推算出M，没有M，就无法解码推出明文。

六、ECC公钥算法的破解难点分析

公开密钥算法总是要基于一个数学上的难题，对于等式：
　　K=kG（其中 K,G为Ep(a,b)上的点，k为小于n（n是点G的阶）的整数）
　　不难发现，给定k和G，根据加法法则，计算K很容易；但给定K和G，求k就相对困难了。而且，p越大越困难，但p越大，计算速度会变慢，200位左右可以满足一般安全要求，

比如居民二代身份证的加密算法采用256位的ECC。
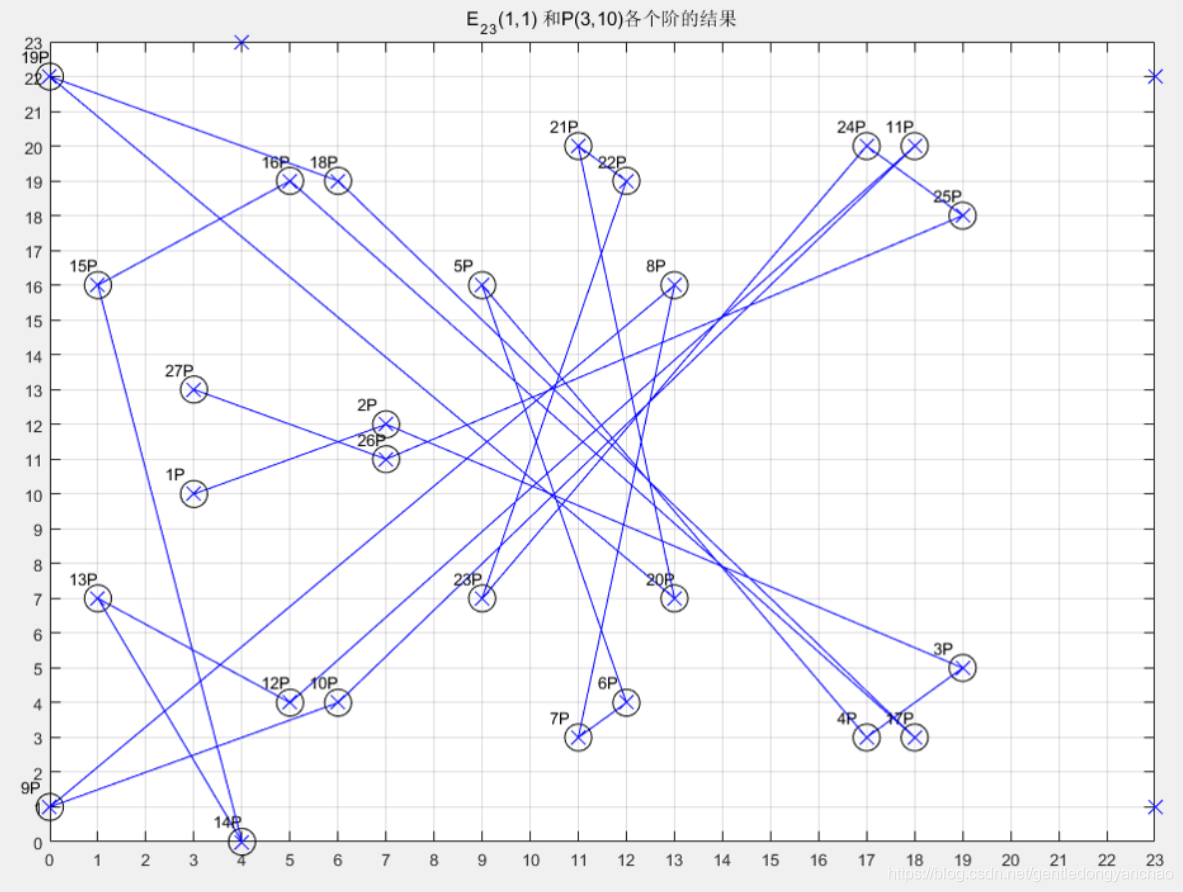
对于更严格的加密场合，把p取得相当大，n也相当大，要把n个解点逐一算出来，采用打表法来破解k，先认同这个思路姑且可行。但G这个基点是用户随意选取的，Ep(a,b)上每个点都可能成为基点，破解者需要建立数不清的新表，椭圆曲线上的G+G+…+G的计算过程很烦躁，离散点的跳跃也错综复杂，有E23(1,1)的P(3,10)为证

这就是椭圆曲线加密算法的破解困难的数学依据，

比特币系统选用的secp256k1中，参数为

p = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
= 2^256 − 2^32 − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 – 1，

n = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141，全是非常大的数字。

七、资料来源

ECC椭圆曲线加密算法原理，https://blog.csdn.net/jingcheng345413/article/details/54969289

ECC椭圆曲线详解（有具体实例），https://www.cnblogs.com/Kalafinaian/p/7392505.html

椭圆曲线算法（ECC）学习（一），http://www.freebuf.com/articles/database/155912.html

有个编码的疑问，说将明文编码到Ep(a,b)上的一个点M，还说编码规则很多。我猜想是将明文中的信息以某种方式记录在点M上，疑问是M就是一个点，可以保存的信息也就是横纵坐标。对于一条明文，比如“hello您好123”，这么长的信息如何记录到一个点M中呢？