设R是一区域，若属于R内任一简单闭曲线的内部都属于R，则称R为单连通区域。更通俗地说，单连通区域是没有“洞”的区域，多连通区域是有“洞”的区域。

格林公式的有效性

　　通过上章的内容，我们知道格林公式有两种表达：

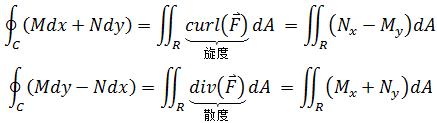
　　尽管物理意义不同，但数学上是相同的，都是把线积分转换为R区域的二重积分。格林公式的成立有个前提条件——向量场需要在R区域处处有定义，更严格地说是F和其导数在R区域处处有定义。如果有一点在向量场中没有定义，就不能简单地使用格林公式，例如：

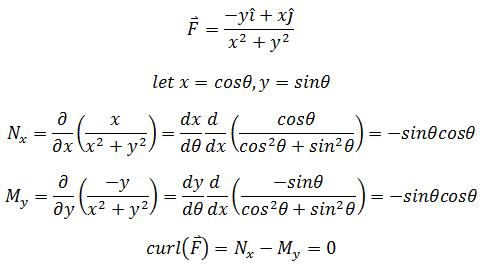
　　F在除原点以外都有意义，且在任意位置旋度都为0。如果在原点处也有定义，这将是个保守场。此时有两种情况，曲线包围了原点和曲线在原点之外：

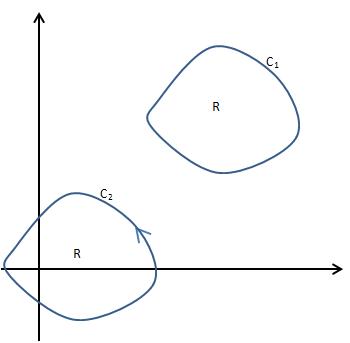
　　其中C₁是独立路径，它的线积分是0；但是C₂只能使最原始的线积分计算。

格林公式的扩展

　　如果在C₂的上挖去原点，那么新的R区域就又满足了格林公式，此时如何计算线积分？

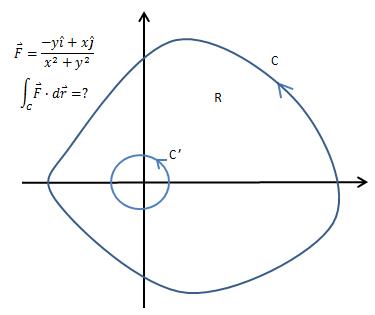
　　如果将连条曲线用两个方向相反的向量链接起来，C和C’就变成了互相联通的一条曲线，如下图所示：

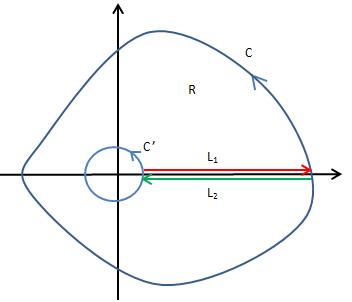
　　点从C’上的一点出发，经过L₁走到C，最后经过L₂回到C’，完成路径的遍历，其中L₁和L₂由于方向相反而互相抵消。所以，R区域的线积分相当于新连通曲线的线积分：

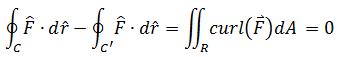
连通区域

　　上一节的R区被称为多连通区域，与之相对的是单连通区域。通俗地说，单连通区域是没有“洞”的区域，多连通区域是有“洞”的区域，这个洞必须在R上：

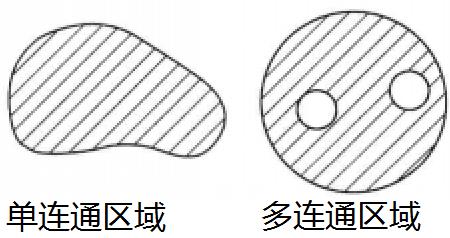
　　如果在连通区域的R上向量场处处有定义且处处可导，就可以使用格林公式或其扩展形式。

 作者：我是8位的