动态规划算法的基本步骤及最长递增子序列问题详解

1、最优子结构：当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质。 
2、重叠子问题：在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只解一次，而后将其解保存在一个表&＃26684;中，在以后尽可能多地利用这些子问题的解。

（二）、动态规划算法的基本步骤设计一个标准的动态规划算法，通常可按以下几个步骤进行：  
1.划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。注意这若干个阶段一定要是有序的或者是可排序的（即无后向性），否则问题就无法用动态规划求解。  
2.选择状态：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。  
3.确定决策并写出状态转移方程：之所以把这两步放在一起，是因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以，如果我们确定了决策，状态转移方程也就写出来了。但事实上，我们常常是反过来做，根据相邻两段的各状态之间的关系来确定决策。  
4.写出规划方程（包括边界条件）：动态规划的基本方程是规划方程的通用形式化表达式。一般说来，只要阶段、状态、决策和状态转移确定了，这一步还是比较简单的。3楼

动态规划的主要难点在于理论上的设计，一旦设计完成，实现部分就会非常简单。根据动态规划的基本方程可以直接递归计算最优&＃20540;，但是一般将其改为递推计算。

  上一篇求解最长递增子序列问题，发现代码有问题，于是重新写了一下进行修改了：

#include
using namespace std;
/*
**该程序针对上一个程序的修改就是：
有一种特殊情况：求状态d[i]时，发现有2个不同的最长子序列
而上面的方法只是保存了其中的一种。
在此程序中为了在一个数组result[i][]中保存多条最长子序列，
我采用了间隔符的方式，PAUSE表示一条子序列的结束，用来间隔
下一条子序列在数组为设置EBD表示后面没有数据了
*/
#define MAXSIZE 100
#define END -100
#define PAUSE -99
int len[MAXSIZE];
int result[MAXSIZE][MAXSIZE];
void LIS(int* a,int n)
{
int i,j,z,k;
int length=1;
result[0][0]=a[0];
result[0][1]=END;
for(i=0;i {
len[i]=1;
for(j=0;j if(a[j]<=a[i]) //当a[j] {
//第一种情况:len[j]+1大于len[i]，此时len[i]对应的状态解集
//应当被覆盖，原来的没用了。
if(len[j]+1>len[i])
{
len[i]=len[j]+1;
for(k=0,z=0;result[j][z]!=END;z++,k++)
{
if(result[j][z]!=PAUSE) //
result[i][k]=result[j][z];
else //PAUSE表示一条记录已结束，下一条开始
{ //此时需要的处理是加入自己a[i]，同时也设置标记符PAUSE
result[i][k++]=a[i];
result[i][k]=PAUSE;
}
}
result[i][k++]=a[i];
result[i][k]=END;
}
//第二种情况，len[j]+1等于len[i]，此时说明，len[i]以前对应的
//result[i][]是有用的，不应该覆盖掉（保留的原因是因为我们题目要求是显示所有的子序列结果）
else if(len[j]+1==len[i])
{
for(k=0;result[i][k]!=END;k++)
;
result[i][k++]=PAUSE;
for(z=0;result[j][z]!=END;z++,k++)
{
if(result[j][z]!=PAUSE) //
result[i][k]=result[j][z];
else //PAUSE表示一条记录已结束，下一条开始
{
result[i][k++]=a[i];
result[i][k]=PAUSE;
}
}
result[i][k++]=a[i];
result[i][k]=END;
}
}
if(length length=len[i];
}
cout<<"长度为:"< for(z=0;z if(len[z]==length)
{
for(i=0;result[z][i]!=END;i++)
{
if(result[z][i]==PAUSE)
{
i++;
cout< }
cout< }
cout< }
}
int main()
{
int a[]={1,3,2,9,11};
LIS(a,5);
return 0;
}
另一个与之相&＃20284;的问题：最长公共子序列问题

一个字符串的子序列，是指从该字符串中去掉任意多个字符后剩下的字符在不改变顺序的情况下组成的新字符串。

最长公共子序列，是指多个字符串可具有的长度最大的公共的子序列。

　动态规划采用二维数组来标识中间计算结果，避免重复的计算来提高效率。

　　　　1)最长公共子序列的长度的动态规划方程

　　　　设有字符串a[0...n]，b[0...m]，下面就是递推公式。字符串a对应的是二维数组num的行，字符串b对应的是二维数组num的列。

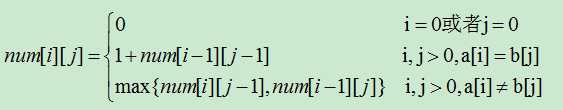
//求最长的公共子序列
#include
#include
using namespace std;
#define MAXSIZE 300
string a;
string b;
int c[MAXSIZE][MAXSIZE];
int d[MAXSIZE][MAXSIZE];
//动态规划的方式求解最长公共子序列问题
void LCS(int m,int n)
{
int i,j;
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)
{
if(a[i-1]==b[j-1])
{
c[i][j]=c[i-1][j-1]+1;
d[i][j]=0;
}
else if(c[i-1][j]>c[i][j-1])
{
c[i][j]=c[i-1][j];
d[i][j]=1;
}
else
{
c[i][j]=c[i][j-1];
d[i][j]=-1;
}
}
}
void display_LCS(int m,int n) //采用回溯方式
{
int i=m,j=n;
int len=c[m][n];
char s[MAXSIZE];
s[len--]=‘\0‘;
while(i>0&&j>0)
{
if(d[i][j]==0)
{
s[len]=a[i-1];
len--;
i--;
j--;
}
else if(d[i][j]==1)
i--;
else
j--;
}
cout<}
int main()
{
a="ABCBDAB";
b="BDCABA";
int m,n;
m=a.size();
n=b.size();
LCS(m,n);
cout< display_LCS(m,n);
return 0;
}

动态规划之最长递增子序列问题详解,布布扣,bubuko.com