时间限制:12000ms
单点时限:6000ms
内存限制:256MB
描述
A市是一个高度规划的城市,但是科技高端发达的地方,居民们也不能忘记运动和锻炼,因此城市规划局在设计A市的时候也要考虑为居民们建造一个活动中心,方便居住在A市的居民们能随时开展运动,锻炼强健的身心。
城市规划局希望活动中心的位置满足以下条件:
1. 到所有居住地的总距离最小。
2. 为了方便活动中心的资源补给和其他器材的维护,活动中心必须建设在A市的主干道上。
为了简化问题,我们将A市摆在二维平面上,城市的主干道看作直角坐标系平的X轴,城市中所有的居住地都可以看成二维平面上的一个点。
现在,A市的城市规划局希望知道活动中心建在哪儿最好。
输入
第一行包括一个数T,表示数据的组数。
接下来包含T组数据,每组数据的第一行包括一个整数N,表示A市共有N处居住地
接下来N行表示每处居住地的坐标。
输出
对于每组数据,输出一行“Case X:
Y”,其中X表示每组数据的编号(从1开始),Y表示活动中心的最优建造位置。我们建议你的输出保留Y到小数点后6位或以上,任何与标准答案的绝对误差或者相对误差在10-6以内的结果都将被视为正确。
数据范围
小数据:1 ≤ T ≤ 1000, 1 ≤ N ≤ 10
大数据:1 ≤ T ≤ 10, 1 ≤ N ≤ 105
对于所有数据,坐标值都是整数且绝对值都不超过106
样例解释
样例1:活动中心的最优建造位置为(1.678787, 0)
- 样例输入
1
3
1 1
2 2
3 3
- 样例输出
Case 1: 1.678787
解析:构建目标函数 f(x),最小值处导数等于 0,但是直接求解较困难。 又因为二次导数恒大于 0
,故其导数变化应该是从负数到 0 到正数。(而目标函数则从递减到递增有最小值。)
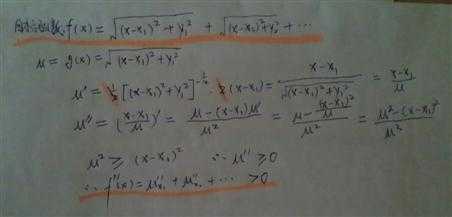
求导数等于 0 时 x 的值。
二分法:
代码(有待查错:)
1 #include
2 //#include <>
3 using namespace std;
4 struct{
5 int x;
6 int y;
7 }points[100001];
8
9 double derivative(int v, int N)
10 {
11 double ans = 0;
12 for(int i = 0; i i)
13 {
14 double t = v - points[i].x;
15 double t2 = sqrt(t * t + points[i].y * points[i].y);
16 ans += t / t2;
17 }
18 return ans;
19 }
20
21 int main()
22 {
23 int T;
24 cin >> T;
25 for(int k = 0; k k)
26 {
27 int a, b;
28 double xMin = 1000000, xMax = -1000000;
29 int N;
30 cin >> N;
31 for(int i = 0; i i)
32 {
33 cin >> a >> b;
34 points[i].x = a;
35 points[i].y = b;
36 if(xMin > a) xMin = a;
37 if(xMax a;
38 }
39 double yl = derivative(xMin, N);
40 double yh = derivative(xMax, N);
41 double xMid;
42 while(fabs(xMax - xMin) >= 1e-6)
43 {
44 xMid = (xMin + xMax) / 2;
45 double tem = derivative(xMid, N);
46 if(tem >= 0)
47 {
48 xMax = xMid;
49 yh = tem;
50 }
51 else
52 {
53 xMin = xMid;
54 yl = tem;
55 }
56 }
57 //cout <<"Case " <
58 printf("Case %d: %.6f", k+1, xMid);
59 }
60 return 0;
61 }