笔记(总结)序列标注问题与求解

在讲述了大量的概率图模型后，本篇介绍下它发挥作用的主要场景——序列标注（Sequence Labaling）。序列包括时间序列以及general sequence，但两者无异。连续的序列在分析时也会先离散化处理。常见的序列有如：时序数据、本文句子、语音数据、等等。常见的序列问题有：

1. 拟合、预测未来节点（走势分析，如股票预测、销量预测等）
2. 判定序列所属类别，即分类问题（如语音识别，判断声音序列所属来源）
3. 判定序列中各个节点的类别，即序列标注问题

我们讨论的是序列标注问题。可以看到，常见的机器学习算法，无论是分类还是回归，都是给定了一个处理对象，然后给定一个整体的标签。而序列标注问题是针对一个处理对象（即序列）对其中的各个部分贴标签，这在处理思路上是完全不同的。传统的序列标注问题主要是用概率图模型求解，而近年来，随着深度学习的发展，适用于序列问题建模的RNN类模型大放异彩。本篇将介绍概率图和RNN-Based的两大类模型。

NLP中的序列标注问题

自然语言处理中，由于主要处理对象是语言，在以句子为单位进行处理时，很自然的就对应到了状态图。句子中不同的“词”（其实是句子中基本元素，可能是词、字或其它语素）就对应着序列的各个节点。句子中各个“词”的出现时有先后关系的，正如说话的过程有的话先说出来有的后说处理，因此这种序列又天然的可以用时间作为序列的测度。所以NLP中的问题通常建模为时间序列问题。许多NLP问题都可以转化为序列标注问题，常见的如：

• 中文分词（Chinese Word Segmentation）：将给定句子切分为具有合理语义的词序列。在分词问题中，序列节点的“词”对应为句子中的每个字，节点的标签空间为{B,I,E,S}。B表示这个字是某个词的开头，I表示这个字是某个词的中间部分，E表示这个字是某个词的结尾，S表示这个字单独成词。每个字最终都会打上对应标签，最终根据标签序列来确定分词结果。
• 词性标注（Part-of-Speech Tagging）：给定已分词的句子，将句子中的所有词标记词性。这里的“词”对应的就是已分词的词序列中的词，节点的标签空间为词性标记空间如{noun,verb,adj,…}。每个词最终都会打上词性标签。
• 命名实体识别（Named Entity Recognition）：找出给定句子中的命名实体（常见的有人名、地名、机构名）。NER问题中，序列节点的“词”对应为句子中的每个字，节点的标签空间为{B,I,E,O}。B表示这个字是某个命名实体的开头，I表示这个字是某个命名实体的中间部分，E表示这个字是某个命名实体的结尾，O表示这个字不属于命名实体部分。根据最后的标签序列确定识别结果。
• ……

概率图模型

由于之前已经比较详细地讲解了各个概率图模型的原理，在此只简要描述问题解决过程。

• 给定隐马尔科夫模型HMM，序列标注问题对应于HMM中的解码问题，即给定观测序列的基础上，如何求隐状态序列。“词”对应的是序列节点，标签对应的是隐状态节点。使用Viterbi算法进行求解，找到概率最大的标签序列作为结果即可。

  顺带一提。HMM中的评估问题，即给定观测序列求其出现的概率，可以对应到是我们上面讲的序列分类问题上。比如语音识别问题，给定音频序列，如何判断是人发出的声音还是狗发出的声音？我们利用人发声的样本集A和狗发声的样本集B分别训练得到两个HMM， λA,λB λ A , λ B 。针对一条新的样本，分别代入两个模型中计算，比较计算出的概率大小，划定为概率较高的模型对应建模类别即可。

• 给定最大熵模型（虽然最大熵模型不属于概率图模型的范畴，但按照之前讲解的顺序还是提一下），最大熵模型利用条件概率 P(Y|X) P ( Y | X ) 直接对标签空间建模。由于最大熵模型基于特征函数，所以在样本构建时，除了原始序列节点外还需要加入每个节点的相关特征。在求解时，最优标签序列为 y∗=argmaxyp(y|x) y ∗ = arg ⁡ max y p ( y | x ) ，注意这里的 y y 不再是单个标签，而是一个标签序列，这是理解概率图建模的关键。

• 给定最大熵马尔可夫模型MEMM，与最大熵模型相同，也是利用条件概率建模，但条件概率的求解中引入了状态的概念。 P(Y|X) P ( Y | X ) 分解为每个状态概率的连乘，每个状态都用一个最大熵模型建模。求解的逻辑与最大熵模型是类似的。

• 给定条件随机场CRF，序列标注问题对应于CRF中的解码问题。CRF也是基于状态，利用特征函数，在全局范围内进行概率归一。CRF由于使用了特征函数，使得其能够挖掘观测序列之间的关系，解决了输出独立性问题；由于使用了全局范围内的概率归一，解决了MEMM的标注偏置问题。求解的逻辑与HMM是类似的，也是使用Viterbi算法求解。

可以看到，CRF综合了HMM、最大熵模型、MEMM的优点，同时解决了它们各自具有的问题，在算法设计是概率图模型中最完备的。实际使用中，序列标注问题上CRF也是概率图模型中效果最好的。

RNN-Based模型

循环神经网络之前也做过总结，下图中，对齐的many-to-many网络架构（最后一个）能够很好的对应到序列标注问题：

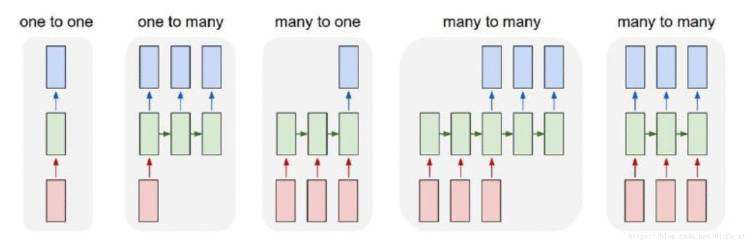
其中，红色的block是输入对应的是待标注的序列，绿色的block是核心网络负责进行特征表示的学习，蓝色的block是标签解码层负责输出对应的标注。核心网络是设计的重点，一般采用的Bidirectional-RNN，双向建模序列能融合上下文的特征。NN模型的优势是通过巨大的参数空间来拟合非线性的关系，但注意到，NN模型的输出也是独立的，这就导致会出现一些不合理的标签序列。比如在分词模型中，出现”B,B”之类的标签段，而这是不合理的标签。

Bi-RNN+CRF

由于RNN-Based模型存在输出独立性问题，我们考虑改进网络结构。参考概率图模型中的最优代表CRF，它通过定义两类特征函数，关联起了前后的隐状态和观测序列。如何将CRF的思想引入神经网络？我们考虑将Bi-RNN得到的表示特征作为观测序列，在输出层（观测序列）上添加一层神经元模拟CRF中隐状态，架构图如下（命名实体识别任务）：

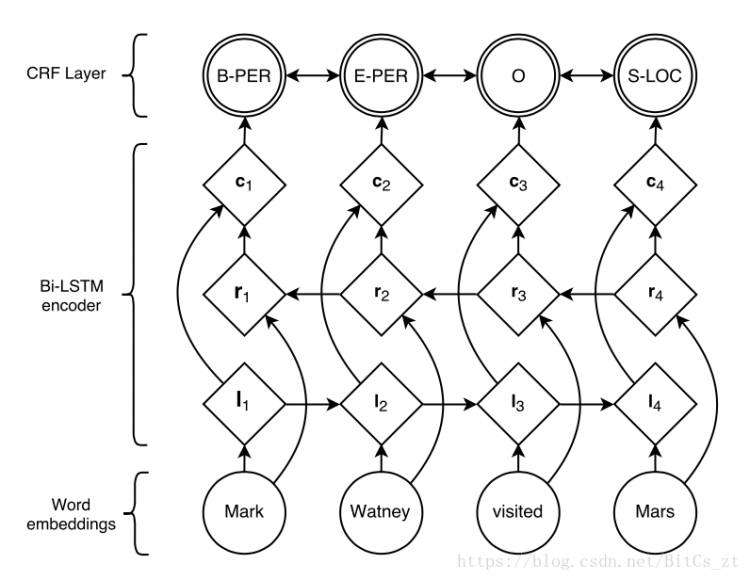
可以看到网络架构是三部分，词向量转化、Bi-RNN特征提取层、CRF层。特征提取层最终输出为 ci=σ(Wcconcat[li,ri]+bc) c i = σ ( W c c o n c a t [ l i , r i ] + b c ) ，把它作为CRF的观测序列。接下来定义CRF的特征函数。类似于HMM，定义状态转移打分矩阵 A A 和状态观测值打分矩阵 P P ，其中 Ai,j A i , j 表示从隐状态 i i 转换到隐状态 j j 的打分， Pk,i P k , i 表示观测值 k k 在隐状态 i i 下的打分。注意，这里的矩阵并不是概率矩阵，因此没有归一化计算。基于这两个矩阵，构造打分函数来模拟CRF的特征函数的打分求和：

s(X,Y)=∑Li=0Ayi,yi+1+∑Li=1Pxi,yi s ( X , Y ) = ∑ i = 0 L A y i , y i + 1 + ∑ i = 1 L P x i , y i

原始的Bi-RNN模型最终的输出是一个向量，向量元素表示各类标签的打分。我们只需要把每个节点的输出向量合并起来，就得到了矩阵 P P 。对应到上述模型架构中，我们只需要将特征 ci c i 映射为一个输出向量 oi o i ，然后拼接起来就得到了 P P 。所以在上述打分函数中， xi x i 实际上指的就是 oi o i ，代表的是序列在位置 i i 的观测值。而矩阵 A A 则建模了标签之间转换的合理性，即可以避免”B,B”这种标签段的出现，解决了输出独立的问题。基于上式的条件概率定义如下：

P(Y|X)=es(X,Y)∑ies(X,Yi) P ( Y | X ) = e s ( X , Y ) ∑ i e s ( X , Y i ) ，

Yi Y i 表示所有可能的标签序列

训练过程的优化目标为：

maxlog(P(Y|X)) max log ⁡ ( P ( Y | X ) )

采用梯度下降法进行BP训练，更新包括 A,P A , P 在内的参数。在预测过程中，前馈计算得到 s(X,Y) s ( X , Y ) ，则标签序列为：

Y∗=argmaxYs(X,Y) Y ∗ = arg ⁡ max Y s ( X , Y )

本篇总结了NLP中的序列标注任务，简要阐述了概率图模型、RNN-Based模型、Bi-LSTM+CRF三类方法的建模过程和建模动机。概率图模型和RNN-Based模型可以参见之前的总结笔记。

参考如下，在此表示感谢：

• 中国科学院大学-自然语言处理（胡玥老师）的课程讲义
• 如何用简单易懂的例子解释条件随机场（CRF）模型？它和HMM有什么区别？
• 论文-Neural Architectures for Named Entity Recognition