BatchNormalization:AcceleratingDeepNetworkTrainingbyReducingInternalCovariateShift论文学习

文章试图解决的问题

• 内部协变量转移(internal covariate shift)&＃xff1a;在训练进行时&＃xff0c;网络中的参数不断改变&＃xff0c;导致每一层的输入分配会进行变化&＃xff0c;这个现象被称作内部协变量转移
• 由于分布变化&＃xff0c;所以需要更小的学习率&＃xff0c;小心的初始化。但导致训练速度降低&＃xff0c;本文就是要解决这个问题
• 内部协变量转移不符合IID(独立同分布)的假设

常见的优化

• 我们都知道&＃xff0c;对初始数据减均值或者白化可以加快学习速度

• • 减均值&＃xff1a;如上b&＃xff0c;紫色的先是拟合线&＃xff0c;但是训练一开始生成的线是在原点的附近&＃xff0c;所以要变成紫色的先要花费较多的时间&＃xff0c;所以我们可以让点都集中在原点的附近—减均值
• • 白化&＃xff1a;白化有很多种方式&＃xff1a;如PCA白化&＃xff1a;
    PCA完后再进行方差归一化—>这样的数据基本满足 0均值&＃xff0c;单位方差和弱相关性。
    • 作者首先考虑对每一层进行PCA白化&＃xff1a;但是这样是不可取的&＃xff0c;因为计算量很大&＃xff0c;而且在求逆的过程中或许不可导
    • 如果只进行简单的对每一层数据归一化&＃xff0c;会降低层的表达能力&＃xff0c;以及梯度的作用。因为在计算梯度的时候没有把归一化的梯度考虑进去。

• 作者想通过Batch Normalization的方式&＃xff1a;尝试减少内部协变量转移&＃xff0c;通过修复层输入的均值和方差来实现。

优点

• 协变量转移减少&＃xff0c;学习速度更快

• 通过减小了网络对梯度的依赖&＃xff0c;使得可以用更大学习率而不存在发散的风险

• 减少了对dropout的需要

内容

• 我们知道对每一层进行白化的不可行&＃xff0c;所以我们考虑做两个必要的简化。

  • 1、我们考虑单独normalize每一个特征&＃xff0c;使其均值为0&＃xff0c;方差为1;而不是在输入输出上共同normalize

  • 对一个d维的input x&＃61;(x(1),...x(d))x&＃61;(x^{(1)},...x^{(d)})x&＃61;(x(1),...x(d))&＃xff0c;我们normalize每一维

  x^(k)&＃61;x(k)−E[x(k)]Var[x(k)]\hat x^{(k)}&＃61;\frac{x^{(k)-E[x^{(k)}]}}{\sqrt{Var[x^{(k)}]}} x^(k)&＃61;Var[x(k)]

  ​x(k)−E[x(k)]​

  • 期望和方差在总体的数据集上计算
  • 仅仅是这一个简化&＃xff0c;就能加速收敛
  • 这个简化导致数据分布是零均值的&＃xff0c;毕竟各层的分布都差不多了

• 我们知道如果只这样干不行&＃xff0c;会降低网络的表达能力&＃xff0c;如在sigmoid之前这样干会把sigmoid非线性极值变成线性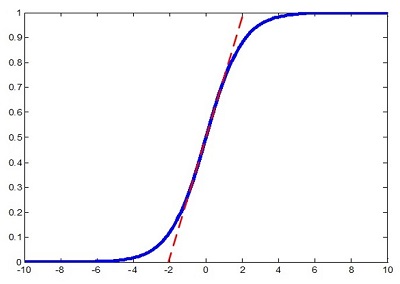

  • 所以我们对每一个激活值x^(k)\hat x^{(k)}x^(k)引进两个参数
    y(k)&＃61;γ(k)x^(k)&＃43;β(k)y^{(k)}&＃61;\gamma^{(k)}\hat x^{(k)}&＃43;\beta^{(k)} y(k)&＃61;γ(k)x^(k)&＃43;β(k)

• 这些参数和原始网络一起学习&＃xff0c;并恢复网络的表达能力

• 事实上&＃xff0c;通过设定γ(k)&＃61;Var[x(k)],β(k)&＃61;E[x(k)\gamma^{(k)}&＃61;\sqrt{Var[x^{(k)}]},\beta^{(k)}&＃61;E[x^{(k)}γ(k)&＃61;Var[x(k)]

  ​,β(k)&＃61;E[x(k)是最理想的方法

  • 2、我们这样设置的训练步骤是基于整个网络的&＃xff0c;&＃xff0c;但是我们在进行SGD的时候是不行的。所以我们有了第二个简化&＃xff1a;我们每次用一个Batch(小批量)的均值和方差来作为对整个数据集的估计

然后我们在测试和训练的时候是不一样的&＃xff0c;因为训练的时候可以用mini_batch&＃xff0c;而测试的时候我们用的是一张张的图片&＃xff0c;所以此时直接用所有的均值和方差来做无偏估计&＃xff0c;然后训练的网络要用net.eval()来使得参数不变

• eval会把网络的参数固定住&＃xff0c;比如dropout和BN的参数&＃xff0c;不会取平均