上岸某中流985,下面主要是数据结构的核心内容:
贪心算法和动态规划的区别
贪心算法:局部最优,划分的每个子问题都最优,得到全局最优,但是不能保证是全局最优解。
动态规划:将问题分解成重复的子问题,每次都寻找左右子问题解中最优的解,一步步得到全局的最优解。
快速排序的算法思想与步骤
二分分治的思想,
对于high,首先从后半部分开始,如果扫描到的值大于基准数据就让high减1,如果发现有元素比该基准数据的值小,就将high位置的值赋值给low位置 ,结果如下:
对于low: 然后开始从前往后扫描,如果扫描到的值小于基准数据就让low加1,如果发现有元素大于基准数据的值(如上图46=>tmp),就再将low位置的值赋值给high位置的值
此外,解释一下归并排序,
稳定的算法有哪些?
归并,插入、冒泡等(记住归并即可)
解决哈希表冲突的办法
1) 线性探测法
2) 平方探测法
3) 伪随机序列法
4) 拉链法
简述 ALV算法与红黑树,B,B+
ALV即平衡二叉树,任何一节点的左子树高度与右子树高度之差不能超过1
优点:减少二叉树元素查找的深度,从而提升平均查找效率。
B树:平衡多路查找树,
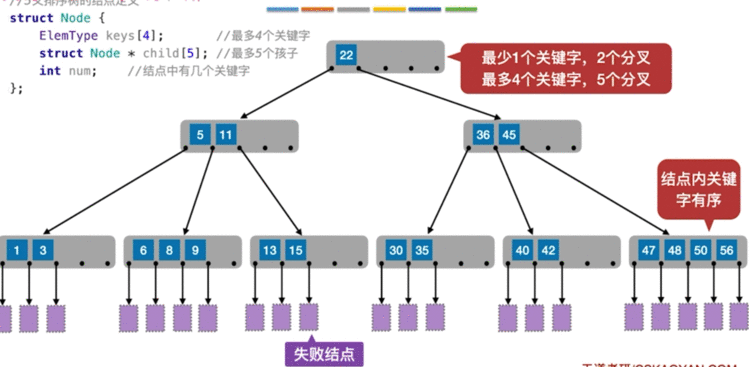
B树的查找方法:
从 B树的根节点出发,在结点的有序表中进行查找,执行如下操作:
①若 Ki 关键字小于 该查询值 ,继续查找
②ki等于 该值 ,查找成功;
③ki大于该值 , 查找 ki左边指针指向的子树 结点并继续查找
④若遍历到结点最后一个关键字 ,查找 ki右边指针指向的子树 结点并继续查找
这样若一直查找到叶节点时,继续查找到失败结点则查找失败
B树优点:
B树一般用来作为磁盘存取的数据结构,定位是磁盘的存取中花费时间比较大的一块,我们可以根据B类树的特点,构造一个多阶的B类树,然后在尽量多的在结点上存储相关的信息,保证层数尽量的少,以便后面我们可以更快的找到信息,磁盘的I/O操作也少一些。
B+树:
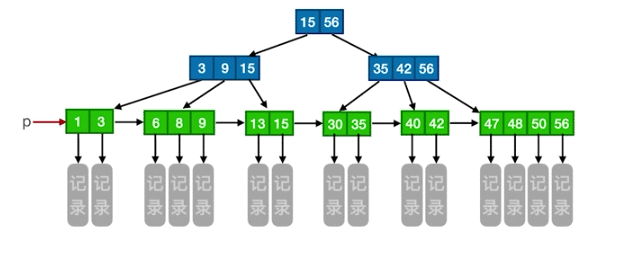
与B树的区别:
| B | B+ |
|---|
| 关键字与分支 | n关键字对应n+1分支 | n关键字对应n分支 |
| 关键字数量 | 叶子结点不包含关键字,不重复 | 叶子结点包含全部关键字 |
| 结点的作用 | B树的任何结点都包含了关键字以及记录的存储地址(也是有记录的) | 非叶子结点的作用是索引作用,只有最大关键字以及指向子树的指针,没有关键字的存储地址 |
| 关键字个数取值范围 | m/2 -1 | m/2 | |
优点:
① 非叶子节点不会带上ROWID,这样,一个块中可以容纳更多的索引项,一是可以降低树的高度。二是一个内部节点可以定位更多的叶子节点。
② B+树中所有叶子节点都是通过指针连接在一起,而B树不会。
红黑树:
从根节点叶子节点的最长路径不能超过最短路径的2倍
希尔排序的思想与步骤
把记录按下标的一定增量分组,若刚开始增量为5 ,则每隔4个元素为1组,组内排序并交换位置。然后增量递减,再次重复上述步骤一直到增量为1 。
此外,还有归并排序,堆排序
简述图,dfs,bfs
一种有边和顶点组成
dfs:
从顶点出发,找到与之相邻未访问的的第一个节点,以该节点为新的起始点,递归操作到相邻节点均已访问,则回溯上一层继续做上述操作。
bfs:从一个顶点出发,依次遍历相邻的未访问的节点,并执行入队操作,接着以队首作为新的起始点作如上操作一直到队列为空。
最小生成树
所有节点都可到达的最短距离和。
prim 和克鲁斯卡尔算法
prim 算法:将边按照权值从小到达依次排序,刚开始是只含有顶点的图,并将当前最小权值的,且连接后不成环边连接,一直连n-1条
克鲁斯卡尔算法:
将顶点分成访问、未访问的两个集合。刚开始所有顶点都在未访问集合里面,
选择一个顶点,放入访问集合
从未访问节点集合里面寻找一顶点,他满足:到访问节点集合中某一点的距离最短,并将该点移到访问集合里。
🅰️ 最短路径
迪杰斯特拉:
算法描述:
初始化:从某一节点出发到各个节点的距离,不相邻则无穷大
接着循环执行如下操作:
① 选择当前最短距离的节点,标记并加入最优路径集合
②计算刚加入的节点A的临近节点B(不包含标记的节点),
若&#xff08;从起始点节点A的距离&#43; A到相邻点B的距离 <当前起始点到B的距离&#xff0c;则更新&#xff09;

floyd 算法&#xff1a;
循环遍历每个顶点V&#xff0c;将v作为中间过程节点&#xff0c;对于每一个&#xff08;i,j) 之间的最短路径&#xff0c;判断&#xff1a;
dis(i,j) > dis(i,v) &#43; dis(v,j) ? dis(i,v) &#43; dis(v,j), dis(i,j)
遍历二叉树&#xff0c;先序中序后序实现办法
后序&#xff1a;
节点入栈到左孩子为空&#xff0c;
若右孩子未访问且不为空&#xff0c;则执行上述步骤
否则&#xff0c;则出栈并访问。
数据结构算法
给定一个单链表&#xff0c;只给出头指针h&#xff1a;
1、如何判断是否存在环&#xff1f;
2、如何知道环的长度&#xff1f;
3、如何找出环的连接点在哪里&#xff1f;
4、带环链表的长度是多少&#xff1f;
1、快慢指针
2、2L &#61; L &#43; x&#xff0c;x&#61;L
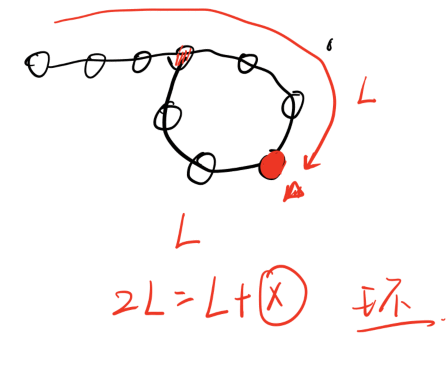
3、在1的基础上&#xff0c;快慢相遇以后&#xff0c;在起始位置再放一个指针&#xff0c;两个指针一倍速前进&#xff0c;相遇的地方就是气质起始位置
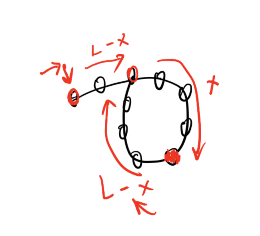
4、在三的基础上&#xff0c;增加一个计数的指
4、在三的基础上&#xff0c;增加一个计数的指针&#xff0c;这样就可以计算出L-x长度&#xff0c; 这样 &#xff0c;L-x&#43;L就是答案。
Topk
① 我们可以选择相应的排序算法进行处理&#xff0c;目前来看快速排序&#xff0c;堆排序和归并排序都能达到O(nlogn)的时间复杂度。
② 堆排序
N个骰子出现和为m的概率
1.现在变量有&#xff1a;骰子个数&#xff0c;点数和。当有k个骰子&#xff0c;点数和为n时&#xff0c;出现次数记为f(k,n)。那与k-1个骰子阶段之间的关系是怎样的&#xff1f;
2.当我有k-1个骰子时&#xff0c;再增加一个骰子&#xff0c;这个骰子的点数只可能为1、2、3、4、5或6。那k个骰子得到点数和为n的情况有&#xff1a;
(k-1,n-1)&#xff1a;第k个骰子投了点数1
(k-1,n-2)&#xff1a;第k个骰子投了点数2
(k-1,n-3)&#xff1a;第k个骰子投了点数3
…
(k-1,n-6)&#xff1a;第k个骰子投了点数6
在k-1个骰子的基础上&#xff0c;再增加一个骰子出现点数和为n的结果只有这6种情况&#xff01;
所以&#xff1a;f(k,n)&#61;f(k-1,n-1)&#43;f(k-1,n-2)&#43;f(k-1,n-3)&#43;f(k-1,n-4)&#43;f(k-1,n-5)&#43;f(k-1,n-6)
3.有1个骰子&#xff0c;f(1,1)&#61;f(1,2)&#61;f(1,3)&#61;f(1,4)&#61;f(1,5)&#61;f(1,6)&#61;1。