白话机器学习算法（二十一）logistic回归

http://blog.csdn.net/wangxin110000/article/details/38112519

我们知道最简单的线性回归 y&＃61;f&＃xff08;x&＃xff09;&＃61;wx&＃43;b,表示随着x的变化&＃xff0c;y会随着变化&＃xff0c;而且是确定的&＃xff0c;即一对一的映射&＃xff0c;x到y的映射

现在有一组<性别&＃xff0c;是否有胡须>&＃xff0c;我们实际上不好确定的说&＃xff0c;男生就一定长胡须&＃xff0c;女生就一定不长胡须&＃xff0c;最好的办法是&＃xff0c;知道了性别是男生后&＃xff0c;我们可以认为&＃xff0c;长胡须的概率比较大。反正如果知道了女生&＃xff0c;那么长胡须的概率比较小。这样子的模型才适合真实情况。

我们希望一个概率模型&＃xff0c;这个模型就是logistic回归模型&＃xff0c;我们假定一个这样的概率模型&＃xff0c;

p(y&＃61;1|x)&＃61;1/(1&＃43;exp(f(x)))

f(x)&＃61;wx&＃43;b

这个模型是分两步的&＃xff0c;

首先x到f&＃xff08;x&＃xff09;的映射&＃xff0c;然后f&＃xff08;x&＃xff09;到p(y&＃61;1|x)

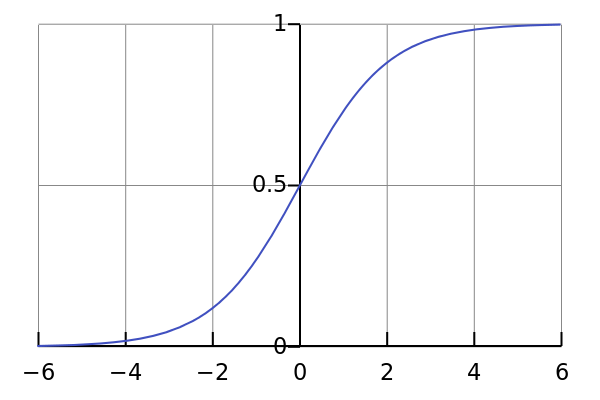
给定训练数据集&＃xff0c;我们可以实际得到p(y&＃61;1|x)的统计值&＃xff0c;这个跟贝叶斯里面是一样的&＃xff0c;

对于如下的式子

p(y&＃61;1|x)&＃61;1/(1&＃43;exp(f(x)))

问题就转化成知道左边&＃xff0c;知道右边方程的形式&＃xff0c;也知道x&＃xff0c;就是不知道w和b&＃xff0c;就变成了一个参数估计的问题了&＃xff0c;怎么求呢&＃xff1f;问题就变成了一个最小二乘法估计的问题。

前面的描述一定有一个问题&＃xff0c;就是这个模型好像是凭空得来的&＃xff0c;是不是所有的数据都可以用这个方法去拟合&＃xff0c;去计算&＃xff1f;

当然不是所有&＃xff0c;但是现实生活中的大部分可以&＃xff0c;logistic经过三个过程&＃xff0c;平缓&＃xff0c;快速&＃xff0c;平缓&＃xff0c;这种模型在经济上&＃xff0c;是非常常见的&＃xff0c;另外举个关于人的幸福感随着收入&＃xff0c;家庭和睦&＃xff0c;父母健康程度&＃xff0c;朋友数目&＃xff0c;等等这些因素变化的例子&＃xff0c;研究表明&＃xff0c;尽管后面因素的增加&＃xff0c;会增加幸福感&＃xff0c;但是不是纯线性递增&＃xff0c;增长有慢有缓。

另外一个逻辑回归的自变量是整个实数域&＃xff0c;因变量是离散的&＃xff0c;这点与分类有所区别。基本上对于属性连续型我们可以用回归&＃xff0c;属性离散的可以用分类。

数据挖掘&＃xff0c;机器学习的算法非常多&＃xff0c;但是不是拿来就用&＃xff0c;应该首先了解算法的特性&＃xff0c;使用范围&＃xff0c;再看数据来源&＃xff0c;什么特点&＃xff0c;这个算法是否符合这种数据&＃xff0c;再决定使用哪种模型

比如聚类算法数十中&＃xff0c;基于图的&＃xff0c;基于概率的&＃xff0c;基于神经网络模型的&＃xff0c;等等&＃xff0c;但是有的算法适合小数据&＃xff0c;有的要求计算矩阵特征值&＃xff0c;有的是多次迭代&＃xff0c;不同的算法有不同的应用范围&＃xff0c;原理不同&＃xff0c;精确度也不同&＃xff0c;计算复杂度也不同&＃xff0c;对于数十上百万的样本集合&＃xff0c;其实可选的模型并不多&＃xff0c;这就要对数据了解&＃xff0c;对模型了解.