AI人工智能学习之回归分析详解

回归分析概述

回归分析是一种统计方法，旨在确定两个或多个变量之间的定量关系。根据涉及的变量数量，回归分析可以分为一元回归和多元回归；根据因变量的数量，可分为简单回归和多重回归；根据自变量和因变量之间的关系类型，可分为线性回归和非线性回归。

回归分析的主要内容包括：
1. 建立数学模型并估计未知参数，常用方法是最小二乘法。
2. 对模型的可信度进行检验。
3. 判断自变量对因变量的影响显著性，通常使用逐步回归、向前回归和向后回归等方法。
4. 利用模型进行预测和控制。

在回归分析中，变量分为因变量和自变量。因变量通常用Y表示，是实际问题中关注的指标；自变量用X表示，影响因变量的取值。

回归分析的主要问题包括：
1. 确定因变量Y与自变量X之间的定量关系，即回归方程。
2. 对回归方程的可信度进行检验。
3. 判断自变量X对因变量Y的影响显著性。
4. 利用回归方程进行预测和控制。

一元线性回归

一元线性回归涉及一个因变量和一个自变量，回归方程为：

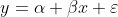   （理论回归方程）

其中，y为因变量，x为自变量，α为截距项，β为回归系数，ε为随机误差项，通常假设ε服从正态分布N(0, σ²)，且与自变量x无关。回归方程描述了y与x之间的线性关系和随机误差。

多元线性回归

多元线性回归考虑多个自变量对因变量的影响。设有p个自变量（x₁, x₂, ..., xₚ），n个观察对象，第i个观察对象的观察值为（yᵢ, xᵢ₁, xᵢ₂, ..., xᵢₚ）。当因变量与自变量组之间存在多重线性关系时，回归模型为：

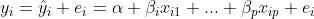
每个因变量的实测值yᵢ由两部分组成：
1. 估计值ŷᵢ，表示因变量的变异中能由自变量决定的部分。
2. 残差eᵢ，表示不由自变量决定的部分，是建模过程中重要的一部分。

残差eᵢ与随机误差项ε不同。随机误差项与观测者、测量工具和被观测物体的性质有关，只能尽量减小但无法避免。残差与预测有关，残差大小衡量预测的准确性。残差越大，预测越不准确。

在多元线性回归中，βₚ表示在其他自变量保持不变的情况下，自变量xₚ每增加一个单位时因变量y的平均增加幅度，称为偏回归系数。

使用多元线性回归进行统计分析时，数据需满足以下条件：
1. 自变量与因变量之间存在线性关系。
2. 各观测间相互独立。
3. 残差eᵢ服从正态分布，方差σ²反映模型的精度，σ越小，预测精度越高。
4. 残差eᵢ的离散程度不随自变量取值水平的改变而改变，即方差齐性。
5. 样本量应为自变量个数的20倍以上，以保证参数估计的稳定性。

具体分析步骤包括：
1. 绘制散点图，观察变量间的趋势。
2. 考察数据分布，进行必要的预处理，如正态性和方差齐性检查。
3. 进行直线回归分析，包括变量的初步筛选和选择方法。

回归方程的拟合度检验
1. 复相关系数R表示模型中所有自变量与因变量y之间线性回归关系的密切程度，取值范围为（0,1），R值越大，线性回归关系越密切。
2. 决定系数R²是一个反应回归直线与样本观测值拟合度的相对指标，表示因变量的变异中能用自变量解释的比例，取值范围为（0,1）。R²越接近1，回归方程拟合度越好。

回归方程的显著性检验
1. F检验用于检验回归方程的总体显著性。
2. t检验用于检验回归系数的个体显著性。

常用回归分析方法
1. 线性回归：适用于因变量为连续变量的情况，自变量可以是连续或离散的，回归线为线性。
2. 逻辑回归：适用于因变量为二元变量的情况，通过Logit函数将概率转换为线性关系。
3. 套索回归（Lasso Regression）：通过惩罚回归系数的绝对值大小，减少模型复杂度，提高预测精度。

通过回归分析进行预测的步骤
1. 收集数据，判断是否可预测。
2. 数据清洗，处理和加工数据。
3. 列出所有变量，确定有效变量。
4. 进行相关分析，确定纳入回归方程的自变量。
5. 确定并消除多重共线性，使用方差膨胀因子（VIF）判断。
6. 求解回归方程，建立预测模型。
7. 计算预测误差，评估模型精度。
8. 进行显著性验证，包括F检验和t检验。
9. 计算置信区间，使用Excel函数TINV、STDEVA和SQRT。
10. 确定预测值，利用回归模型计算预测值并进行综合分析。