3.223.28周学习总结中的贪心作业收获及困惑

这周A了贪心作业里我能看懂并且有想法的题&＃xff0c;当然&＃xff0c;期间参考了很多别人的代码。不过我参考的前提是&＃xff0c;我要先读懂题目并且有解题的想法。对于题目看不懂或者一点思绪也没有的题目&＃xff0c;我也不会参考题解&＃xff0c;我觉得这一点用也没有。

作业中收获最大的是一点也不像贪心的A题&＃xff0c;一上来就把我打懵了。

INPUT DETAILS:

There are five cows at locations 1, 5, 3, 2, and 4.

OUTPUT DETAILS:

Cow at 1 contributes 1&＃43;2&＃43;3&＃43;4&＃61;10, cow at 5 contributes 4&＃43;3&＃43;2&＃43;1&＃61;10, cow at 3 contributes 2&＃43;1&＃43;1&＃43;2&＃61;6, cow at 2 contributes 1&＃43;1&＃43;2&＃43;3&＃61;7, and cow at 4 contributes 3&＃43;2&＃43;1&＃43;1&＃61;7. The total volume is (10&＃43;10&＃43;6&＃43;7&＃43;7) &＃61; 40.

见到这道题时&＃xff0c;input details让我有点疑惑locations是不是有什么玄机——比如five cows&＃xff0c;但分别在2、45、33、25、67&＃xff08;即随机数&＃xff09;locations分布。不过事实证明&＃xff0c;我真的code啥啥不行&＃xff0c;瞎想第一名&＃xff0c;压根就没这回事。

想通题目是怎么回事之后&＃xff0c;第一个很low的思路就很清晰了——用两层for循环&＃xff0c;第一层从第一头牛往后数&＃xff0c;第二头牛从最后一头牛往前数&＃xff0c;取两者差的绝对值&＃xff0c;那就是第一头牛和其他牛的位置差&＃xff0c;然后是第二头牛……最后累加起来就是所要的答案了。这是我这个笨比绞尽脑汁才想到的笨办法。

#include
#include
using namespace std;
int main()
{int x;scanf("%d", &x);long long a[10010] &＃61; {0};long long sum &＃61; 0;int i &＃61; 0;while(i&＃61; 0; j--) //刚开始代码是j>0if (a[j] >&＃61; a[i]) //这样忽略了第一只牛sum &＃43;&＃61; a[j] - a[i]; //第一次使用的是abs&＃xff08;&＃xff09;else //但提交之后报错sum &＃43;&＃61; a[i] - a[j];}printf("%lld", sum);system("pause");
}

TLETLETLE&＃xff0c;超时的原因很显而易见的是两个for让复杂度成为O(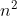)。原本使用的是cin和cout&＃xff0c;我尝试了ios_base::sync_with_stdio(false)关闭了缓冲同步&＃xff0c;但是编译报错&＃xff0c;原因google之后还是不清楚&＃xff0c;后来发现这玩意要放在int main()函数里&＃xff01;&＃xff01;&＃xff01;所以我只好改用scanf和printf&＃xff0c;不过依然TLE了&＃xff0c;说明不是输入输出问题&＃xff0c;只能从修改算法入手。

我想起了ZJU的陈越教授讲数据结构时提到的一个例子&＃xff0c;她用递归代替双层for循环&＃xff0c;节约了大量时间&＃xff0c;所以我决定试试递归&＃xff08;但是我不会啊&＃xff09;……最后想到的办法——在[0,i)区间内的j其实是(i,x]的绝对值嘛&＃xff0c;那就不循环它&＃xff0c;直接把一半翻倍就行。

#include
#include
using namespace std;
int main()
{ios::sync_with_stdio(false);int x;cin>>x;long long a[10010] &＃61; {0};long long sum &＃61; 0;int i &＃61; 0;while(i>a[i];i&＃43;&＃43;;}sort(a, a &＃43; x);for (int i &＃61; 0; i i ; j--)sum &＃43;&＃61; a[j] - a[i];}cout<}

这道题暴露的问题就很明显了&＃xff1a;

1.正确理解题目的意思

2.循环条件和结果之间的关系

3.递归的使用

这三点都是现在我急需深入理解并突破的。

周四打了第一场CF&＃xff0c;我以为能A两题&＃xff0c;结果只有一题出结果&＃xff0c;另一道写了一半就时间到了。

同样是A题&＃xff0c;花了一堆时间才读懂了题意。想到可以用单元格编号推出所在的行列&＃xff0c;再计算出它的值。

这倒是不难&＃xff0c;对于先行后列来讲&＃xff0c;单元格序号模行数后的余数就是单元格所在的行数&＃xff0c;单元格除以行数再加1就得出了所在的列数&＃xff0c;但是存在例外存在&＃xff0c;当单元格在最后一行时&＃xff0c;需要改进。

最后的代码如下&＃xff1a;

#include
using namespace std;
unsigned long long n, m, x, mx, nx, ans;
int main()
{ios::sync_with_stdio(false);int t;cin >> t;while (t){cin >> n >> m >> x;if (x % n &＃61;&＃61; 0){nx &＃61; x / (x / n);mx &＃61; x / n;}else{nx &＃61; x % n;mx &＃61; x / n &＃43; 1;}ans &＃61;(nx - 1) * m &＃43; mx;cout <}

不过我感觉这段代码好像哪里还是有问题的&＃xff0c;在写博客的时候又觉得有些细节想不通&＃xff0c;但是能AC&＃xff0c;就很奇怪。

这周刷的题还是比较多的&＃xff0c;下周想先过一下枚举、递归与分治、二分、三分、分数规划的内容&＃xff0c;先大致了解一下&＃xff01;当然了&＃xff0c;每天睡前A1-2道题也是必须的。