1&＃xff0c;cf Game with Chips&＃xff1b;2&＃xff0c;acwing 243.一个简单的整数问题2&＃xff08;线段树&＃xff09;&＃xff1b;3&＃xff0c;亚特兰蒂斯&＃xff08;扫描线&＃xff09;&＃xff1b;4&＃xff0c;维护序列&＃xff1b;
题意&＃xff1a;给你n x m的棋盘&＃xff0c;有k个芯片分布在棋盘上&＃xff0c;操作是左右上下各平移一格&＃xff0c;要求第i个芯片至少经过一次给定位置&＃xff1b;芯片遇到墙后&＃xff0c;若仍往墙的方向走&＃xff0c;则会不动&＃xff1b;多个芯片可以在同一格&＃xff1b;
操作次数不超过2nm次&＃xff1b;
输出操作序列和操作步数&＃xff1b;没有序列输出-1&＃xff1b;
思路&＃xff1a;直接将所有的芯片先移动到&＃xff08;1&＃xff0c;1&＃xff09;在带着整体一个个走&＃xff0c;遍历一遍棋盘&＃xff0c;必能完成要求&＃xff1b;
而且不会超过2nm&＃xff1b;
#include
#define rep1(i,a,n) for(ll i&＃61;a;i#define rep2(i,a,n) for(ll i&＃61;a;i<&＃61;n;i&＃43;&＃43;)
#define per1(i,n,a) for(ll i&＃61;n;i>a;i--)
#define per2(i,n,a) for(ll i&＃61;n;i>&＃61;a;i--)
#define quick_cin() cin.tie(0),cout.tie(0),ios::sync_with_stdio(false)
#define INF 0x3f3f3f3f
#define pb push_back
#define endl "\n"
using namespace std;
typedef long long ll;
typedef pair PII;
typedef double db;
int n,m,k;
string ans;
signed main()
{quick_cin();cin>>n>>m>>k;int maxx&＃61;0,maxy&＃61;0;rep2(i,1,k){int x,y;cin>>x>>y;maxx&＃61;max(maxx,x);maxy&＃61;max(maxy,y);}rep2(i,1,maxx-1)ans&＃43;&＃61;"U";rep2(i,1,maxy-1)ans&＃43;&＃61;"L";rep2(i,1,k){int edx,edy;cin>>edx>>edy;}rep2(i,1,n){rep2(j,1,m-1){if(i%2)ans&＃43;&＃61;&＃39;R&＃39;;else ans&＃43;&＃61;&＃39;L&＃39;;}if(i}
2&＃xff0c;一个简单的整数问题2&＃xff1b;
#include
#define rep1(i,a,n) for(ll i&＃61;a;i#define rep2(i,a,n) for(ll i&＃61;a;i<&＃61;n;i&＃43;&＃43;)
#define per1(i,n,a) for(ll i&＃61;n;i>a;i--)
#define per2(i,n,a) for(ll i&＃61;n;i>&＃61;a;i--)
#define quick_cin() cin.tie(0),cout.tie(0),ios::sync_with_stdio(false)
#define INF 0x3f3f3f3f
#define pb push_back
#define endl "\n"
using namespace std;
typedef long long ll;
typedef pair PII;
typedef double db;
const int N&＃61;1e5&＃43;10;
int n,m;
int w[N];
struct node
{int l,r;ll sum,add;
}tr[N*4];
void pushup(int u)
{tr[u].sum&＃61;tr[u<<1].sum&＃43;tr[u<<1|1].sum;
}
void pushdown(int u)
{node &root&＃61;tr[u],&left&＃61;tr[u<<1],&right&＃61;tr[u<<1|1];if(root.add){left.add&＃43;&＃61;root.add,left.sum&＃43;&＃61;(ll)(left.r-left.l&＃43;1)*root.add;right.add&＃43;&＃61;root.add,right.sum&＃43;&＃61;(ll)(right.r-right.l&＃43;1)*root.add;root.add&＃61;0;}
}
void build(int u,int l,int r)
{if(l&＃61;&＃61;r)tr[u]&＃61;{l,r,w[r]};else{tr[u]&＃61;{l,r};int mid&＃61;l&＃43;r>>1;build(u<<1,l,mid),build(u<<1|1,mid&＃43;1,r);pushup(u);}
}
void modify(int u,int l,int r,int d)
{if(tr[u].l>&＃61;l&&tr[u].r<&＃61;r){tr[u].sum&＃43;&＃61;(ll)(tr[u].r-tr[u].l&＃43;1)*d;tr[u].add&＃43;&＃61;d;}else{pushdown(u);int mid&＃61;tr[u].l&＃43;tr[u].r>>1;if(l<&＃61;mid)modify(u<<1,l,r,d);if(r>mid)modify(u<<1|1,l,r,d);pushup(u);}
}
ll query(int u,int l,int r)
{if(tr[u].l>&＃61;l&&tr[u].r<&＃61;r)return tr[u].sum;else{pushdown(u);int mid&＃61;tr[u].l&＃43;tr[u].r>>1;ll sum&＃61;0;if(l<&＃61;mid)sum&＃61;query(u<<1,l,r);if(r>mid)sum&＃43;&＃61;query(u<<1|1,l,r);return sum;}
}
signed main()
{quick_cin();cin>>n>>m;rep2(i,1,n)cin>>w[i];build(1,1,n);char c;int l,r,d;while(m--){cin>>c>>l>>r;if(c&＃61;&＃61;&＃39;C&＃39;){cin>>d;modify(1,l,r,d);}else cout<}
3&＃xff0c;亚特兰蒂斯&＃xff1b;
直接学这种方法是怎么实现和解决问题的&＃xff1a;
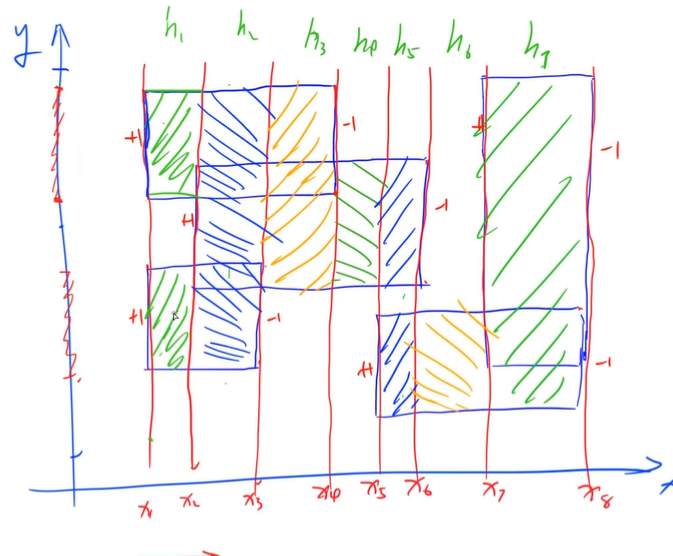
就是用垂直x轴的线从左往右扫&＃xff0c;得到的线段长度*宽度&＃xff08;xi-xi-1&＃xff09;&＃xff0c;即为小矩阵的面积&＃xff0c;求和即为所有的面积且不重复&＃xff1b;
那么怎么实现线段长度的更新呢&＃xff1f;换言之&＃xff0c;如何保证线段长度正确合理呢&＃xff1f;
对每次输入的矩形&＃xff0c;左边打上&＃43;1的标记&＃xff0c;右边打上-1的标记&＃xff0c;这样加1之后&＃xff0c;只要该段区间所有地方都>0&＃xff0c;就说明该区间可以被当作长度&＃xff0c;知道遇到它原来的右边界&＃xff0c;然后减去1&＃xff0c;表示该矩形不再贡献长度&＃xff1b;
由此产生两个操作&＃xff1a;
k&＃61;1或-1&＃xff1b;
统计信息只往下看&＃xff01;&＃xff01;&＃xff1b;
特殊性&＃xff1a;
因为只看最终找到的长度&＃xff0c;所有区间查询只看tr[1]&＃xff0c;根节点的长度信息&＃xff1b;
二是操作都是成对的&＃xff0c;即&＃xff08;1&＃xff0c;5&＃xff09;&＃43;1&＃xff0c;之后一定会&＃xff08;1&＃xff0c;5&＃xff09;-1&＃xff1b;
综上&＃xff0c;不需要pushdown来分裂区间&＃xff0c;也可以保证答案的正确性&＃xff1b;
因为xy可能是小数&＃xff0c;所以需要离散化&＃xff01;&＃xff01;&＃xff1b;
#include
#define rep1(i,a,n) for(ll i&＃61;a;i#define rep2(i,a,n) for(ll i&＃61;a;i<&＃61;n;i&＃43;&＃43;)
#define per1(i,n,a) for(ll i&＃61;n;i>a;i--)
#define per2(i,n,a) for(ll i&＃61;n;i>&＃61;a;i--)
#define quick_cin() cin.tie(0),cout.tie(0),ios::sync_with_stdio(false)
#define INF 0x3f3f3f3f
#define pb push_back
#define endl "\n"
using namespace std;
typedef long long ll;
typedef pair PII;
typedef double db;
const int N&＃61;1e5&＃43;10;
int n;
struct segment
{db x,y1,y2;int k;bool operator<(const segment &t)const{return x}seg[N*2];
struct node
{int l,r;int cnt;db len;
}tr[N*8];
vectorys;
int find(db y)
{return lower_bound(ys.begin(),ys.end(),y)-ys.begin();
}
void pushup(int u)
{if(tr[u].cnt)tr[u].len&＃61;ys[tr[u].r&＃43;1]-ys[tr[u].l];else if(tr[u].l!&＃61;tr[u].r){tr[u].len&＃61;tr[u<<1].len&＃43;tr[u<<1|1].len;}else tr[u].len&＃61;0;
}
void build(int u,int l,int r)
{tr[u]&＃61;{l,r,0,0};if(l!&＃61;r){int mid&＃61;l&＃43;r>>1;build(u<<1,l,mid),build(u<<1|1,mid&＃43;1,r);}
}
void modify(int u,int l,int r,int k)
{if(tr[u].l>&＃61;l&&tr[u].r<&＃61;r){tr[u].cnt&＃43;&＃61;k;pushup(u);}else{int mid&＃61;tr[u].l&＃43;tr[u].r>>1;if(l<&＃61;mid)modify(u<<1,l,r,k);if(r>mid)modify(u<<1|1,l,r,k);pushup(u);}
}
signed main()
{quick_cin();int T&＃61;0;while(cin>>n,n){ T&＃43;&＃43;;ys.clear();int j&＃61;0;rep1(i,0,n){db x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;seg[j&＃43;&＃43;]&＃61;{x1,y1,y2,1};seg[j&＃43;&＃43;]&＃61;{x2,y1,y2,-1};ys.pb(y1);ys.pb(y2);}sort(ys.begin(),ys.end());ys.erase(unique(ys.begin(),ys.end()),ys.end());//去重build(1,0,ys.size()-2);//区间比点的个数少1&＃xff1b;sort(seg,seg&＃43;n*2);double ans&＃61;0;rep1(i,0,n*2){if(i>0)ans&＃43;&＃61;tr[1].len*(seg[i].x-seg[i-1].x);modify(1,find(seg[i].y1),find(seg[i].y2)-1,seg[i].k);}cout<<"Test case #"<}
4&＃xff0c;维护序列&＃xff1b;
两个懒标记add 和 mul&＃xff1b;
sum的维护&＃xff1b;用x*mul&＃43;add的形式来维护&＃xff0c;这样形式上很统一&＃xff0c;并且可以互相转化&＃xff1b;默认mul是1&＃xff0c;add是0&＃xff1b;
只乘一个数x&＃xff0c;mul&＃61;x&＃xff0c;add&＃61;0&＃xff0c;只加一个数x&＃xff1a;mul&＃61;1&＃xff0c;add&＃43;&＃61;x&＃xff1b;
都有&＃xff1a;
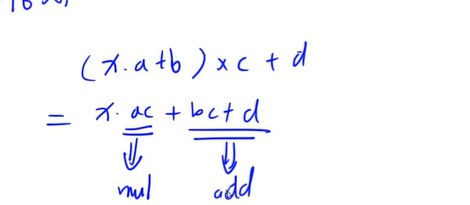
把mul&＃61;a变成ac&＃xff0c;add&＃61;b变成bc&＃43;d&＃xff1b;
#include
#define rep1(i,a,n) for(ll i&＃61;a;i#define rep2(i,a,n) for(ll i&＃61;a;i<&＃61;n;i&＃43;&＃43;)
#define per1(i,n,a) for(ll i&＃61;n;i>a;i--)
#define per2(i,n,a) for(ll i&＃61;n;i>&＃61;a;i--)
#define quick_cin() cin.tie(0),cout.tie(0),ios::sync_with_stdio(false)
#define INF 0x3f3f3f3f
#define pb push_back
#define endl "\n"
using namespace std;
typedef long long ll;
typedef pair PII;
typedef double db;
const int N&＃61;1e5&＃43;10;
int w[N];
int n,p,m;
struct node
{int l,r;int sum,add,mul;
}tr[N*4];
void pushup(int u)
{tr[u].sum&＃61;(tr[u<<1].sum&＃43;tr[u<<1|1].sum)%p;
}
void eval(node &t,int add,int mul)
{t.sum&＃61;((ll)t.sum*mul&＃43;(ll)(t.r-t.l&＃43;1)*add)%p;t.mul&＃61;((ll)t.mul*mul)%p;t.add&＃61;((ll)t.add*mul&＃43;add)%p;
}
void pushdown(int u)
{eval(tr[u<<1],tr[u].add,tr[u].mul);eval(tr[u<<1|1],tr[u].add,tr[u].mul);tr[u].add&＃61;0,tr[u].mul&＃61;1;
}
void build(int u,int l,int r)
{if(l&＃61;&＃61;r)tr[u]&＃61;{l,r,w[r],0,1};else{tr[u]&＃61;{l,r,0,0,1};int mid&＃61;l&＃43;r>>1;build(u<<1,l,mid),build(u<<1|1,mid&＃43;1,r);pushup(u);}
}
void modify(int u,int l,int r,int add,int mul)
{if(tr[u].l>&＃61;l&&tr[u].r<&＃61;r)eval(tr[u],add,mul);else{pushdown(u);int mid&＃61;tr[u].l&＃43;tr[u].r>>1;if(l<&＃61;mid)modify(u<<1,l,r,add,mul);if(r>mid)modify(u<<1|1,l,r,add,mul);pushup(u);}
}
int query(int u,int l,int r)
{if(tr[u].l>&＃61;l&&tr[u].r<&＃61;r)return tr[u].sum;pushdown(u);int mid&＃61;tr[u].l&＃43;tr[u].r>>1;int sum&＃61;0;if(l<&＃61;mid)sum&＃61;query(u<<1,l,r);if(r>mid)sum&＃61;(sum&＃43;query(u<<1|1,l,r))%p;return sum;
}
signed main()
{quick_cin();cin>>n>>p;rep2(i,1,n)cin>>w[i];cin>>m;int c,l,r,d;build(1,1,n);while(m--){cin>>c>>l>>r;if(c&＃61;&＃61;1){cin>>d;modify(1,l,r,0,d);}else if(c&＃61;&＃61;2){cin>>d;modify(1,l,r,d,1);}else cout<}
京公网安备 11010802041100号