20210304力扣根据前序遍历和中序遍历确定二叉树快速排序思想

力扣 根据前序遍历和中序遍历确定二叉树


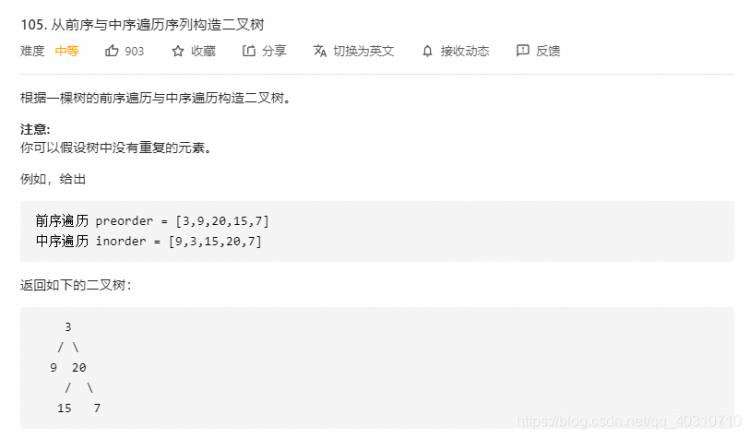
基本思路
前序遍历确定根节点是哪个（第一个就是根节点）
中序遍历根据已知根节点确定左右子树的元素组成
根节点左 左子树
根节点右 右子树
再根据前序遍历确定 左子树的根节点
根据左子树的根节点确定 左子树元素的左右子树

理解：每次更新的是提供的前序遍历序列和中序遍历序列 ，官方答案提供的是更新索引，不更新前、中序遍历
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder.length==0 || inorder.length==0) {
return null;
}
//根据前序数组的第一个元素，就可以确定根节点
TreeNode root = new TreeNode(preorder[0]);
for(int i=0;i<preorder.length;++i) {
//用preorder[0]去中序数组中查找对应的元素
if(preorder[0]==inorder[i]) {
//将前序数组分成左右两半，再将中序数组分成左右两半
//之后递归的处理前序数组的左边部分和中序数组的左边部分
//递归处理前序数组右边部分和中序数组右边部分
int[] pre_left = Arrays.copyOfRange(preorder,1,i+1);
int[] pre_right = Arrays.copyOfRange(preorder,i+1,preorder.length);
int[] in_left = Arrays.copyOfRange(inorder,0,i);
int[] in_right = Arrays.copyOfRange(inorder,i+1,inorder.length);
root.left = buildTree(pre_left,in_left);
root.right = buildTree(pre_right,in_right);
break;
}
}
return root;
}
}


class Solution {
public int numSquares(int n) {
int[] dp = new int[n + 1]; // 默认初始化值都为0
for (int i = 1; i <= n; i++) {
dp[i] = i; // 最坏的情况就是每次+1
for (int j = 1; i - j * j >= 0; j++) {
dp[i] = Math.min(dp[i], dp[i - j * j] + 1); // 动态转移
//dp[0]=0，当i-j*j=0时，说明只需要一次就可以，如果i-j*j！=0时，说明我们需要根据前面的最优结果进行+1
//例如5 因为4的最优只有1个即可，因此5只需在4的基础上+1
}
}
return dp[n];
}
}


快速排序思想
1、第一轮 最左侧元素作为Key值（目标：>Key 右侧， 双指针放在第二个元素和最后一个元素
（1）从r指针开始，寻找小于Key的元素，找到时停下
（2）从l指针开始，寻找大于Key的元素，找到时停下，交换l、r指针元素的位置
（3）重复（1）直到左右指针重合（l=r）
（4）重合后将l指针元素与Key交换顺序（实现了左Key）
2、将Key左侧的作为新的待排列的数组，重复1操作
将Key右侧的作为新的待排列的数组，重复1操作
3、排列完成标志 l>r或者输入数组为空时说明排列完成

class Solution {
public void sortColors(int[] nums) {
int len = nums.length;
quicksort(nums,0,len-1);
}
public int[] quicksort(int[] nums,int start,int end){
if(start>end){
return nums;
}
int Key = nums[start];
int left = start;
int right = end;
while(left<right){
while(left<right&&nums[right]>=Key){ //从右向左找到
right--;
}
while(left<right&&nums[left]<=Key){ //从左向右找到>Key的值终止循环
left++;
}
if(left<right){
swap(nums,left,right);
}
if(left>=right){
swap(nums,start,left);
}
}
quicksort(nums,left+1,end);
quicksort(nums,start,left-1);
return nums;
}
public void swap(int[] nums, int a, int b){
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}


归并排序 核心思想（两两有序合并）
1、将序列中待排序数字分为若干组，每个数字分为一组
2、将若干个组凉凉合并，保证合并后的数组是有序的
3、重复第二部操直到只剩下一组

两两合并原则：，比较两组数据头部大小，将小的放入新的序列，更新头部指针，重复操作