08对偶理论以及灵敏度分析

 1.对偶问题的提出

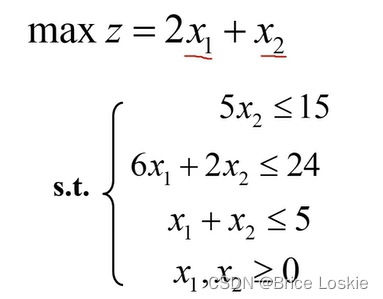
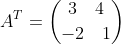
s.t. 

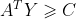
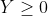
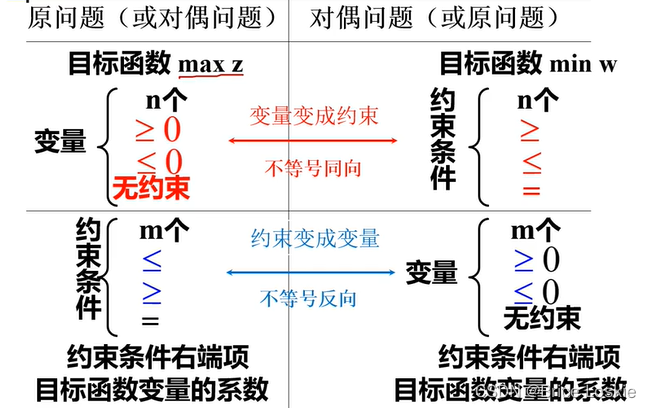
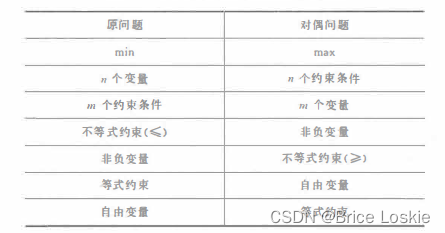
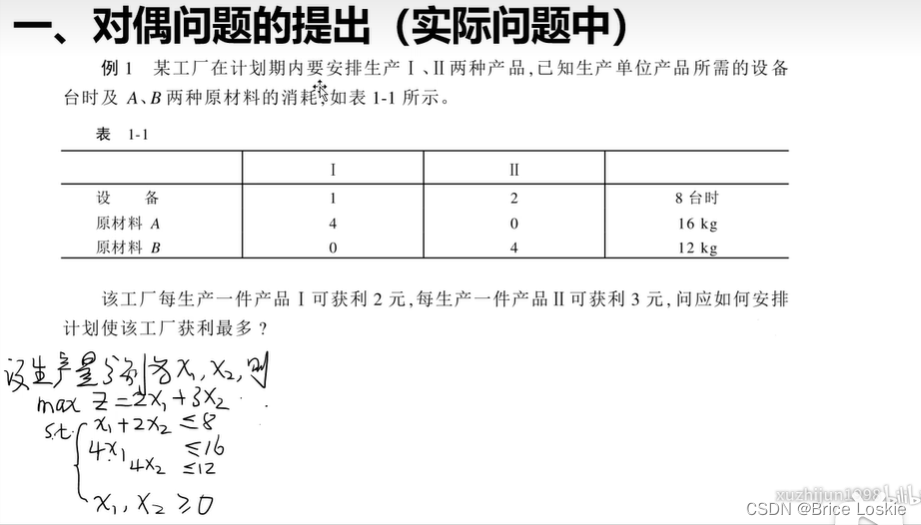
·        原问题为max 对偶问题是min的条件下 我们来看目标函数之间的关系  

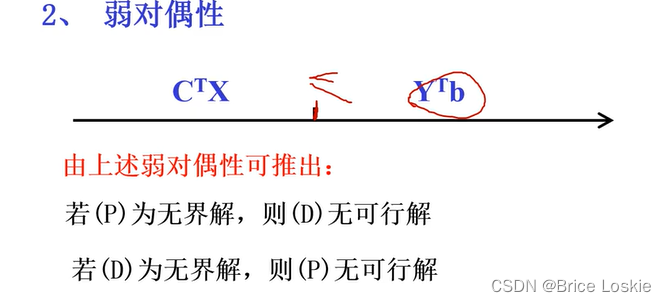
 无界解指的是C^TX可以取得无穷大

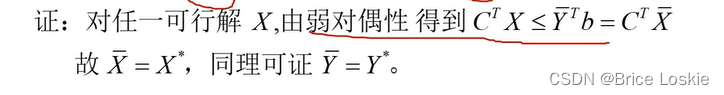
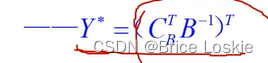
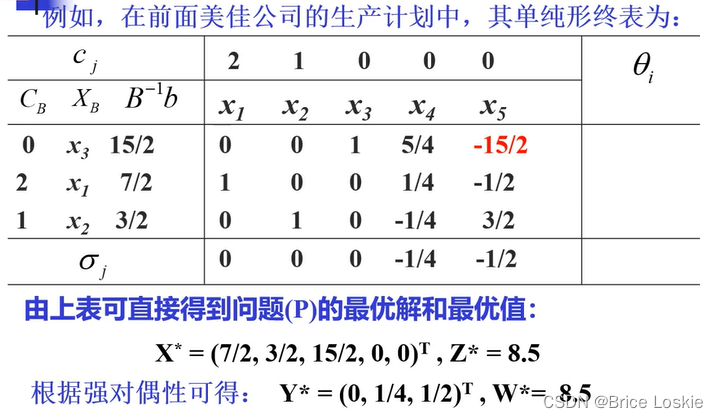
 问题  Y^*是如何得到的

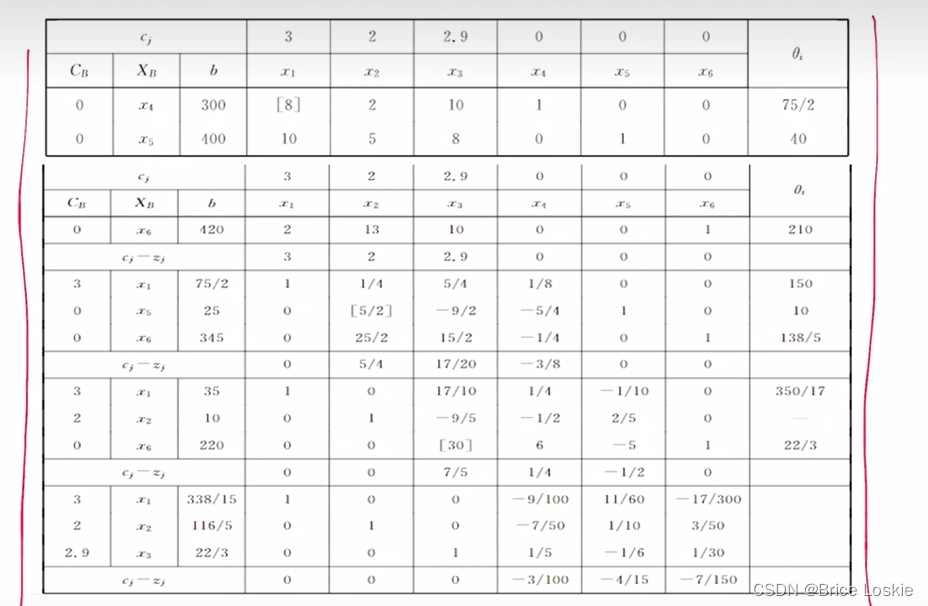
 我们求的是正的检验数，他是以目标函数max开始的，所以这里是负的检验数字，我们这里需要把检验数变为正，所以 

 对偶单纯形法

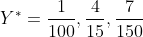
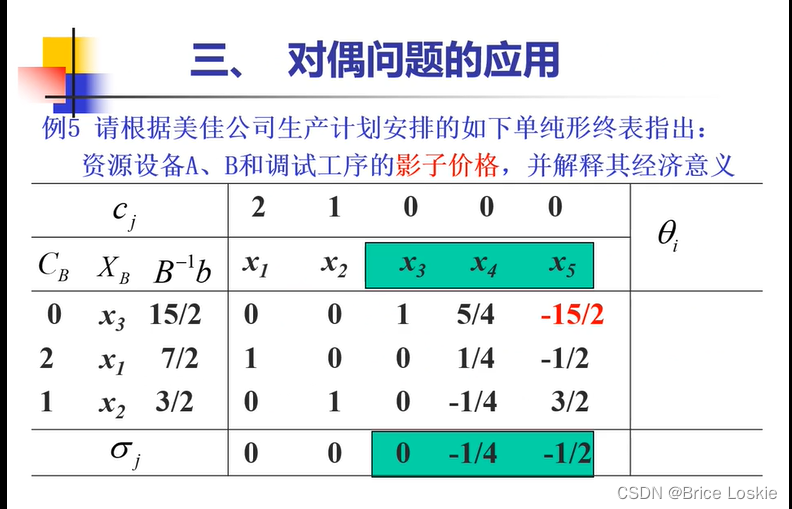
 最后的解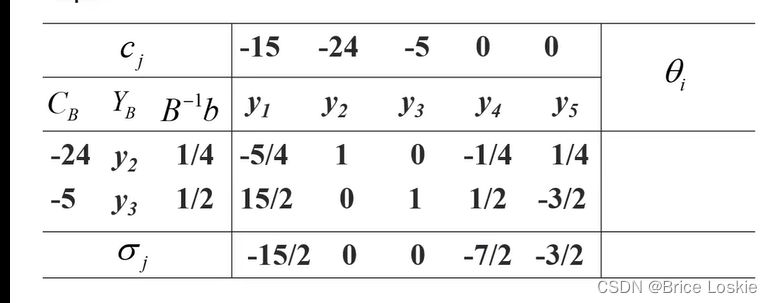

Y*=(0,1/4,1/2,0,0) w*=8.5

 灵敏度分析

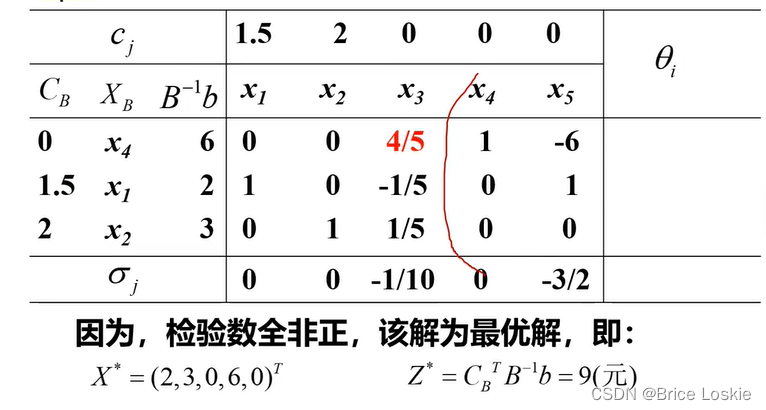
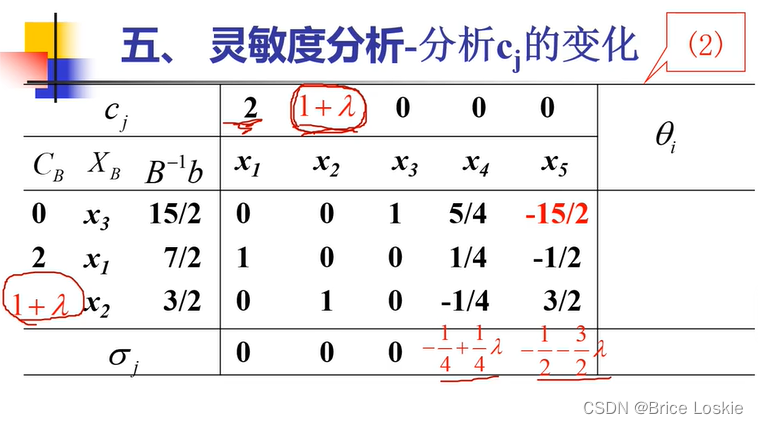
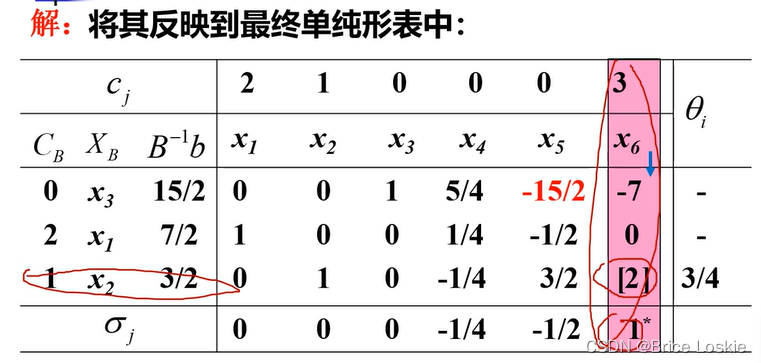
 但是搞出来却是14

怎么组合呢

对偶问题的性质

1.对称性

对偶的对偶是原问题

2.弱对偶性

原问题的任意一个目标值(max)不超过对偶问题任意一个目标值

3.无界性

       原问题(max)为无穷大(无界)，则对偶问题无可行解

       原问题(max)不可行,对偶问题或者无界，或者不可行

原问题无界 => 对偶问题不可行

原问题不可行≠>对偶问题无界

4. 原问题有最优值，则对偶问题也有最优值且相同

5.互补松弛性(松紧定理)

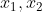 存在某种关系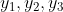

紧：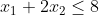

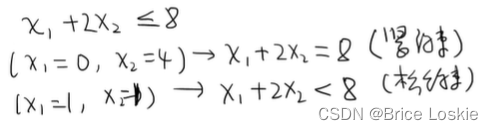
 举例说明：

如果一个解满足

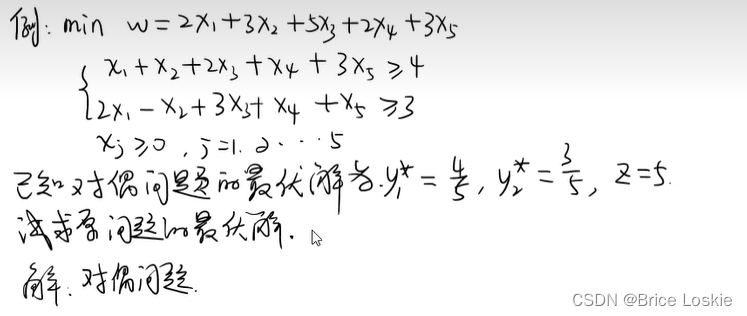
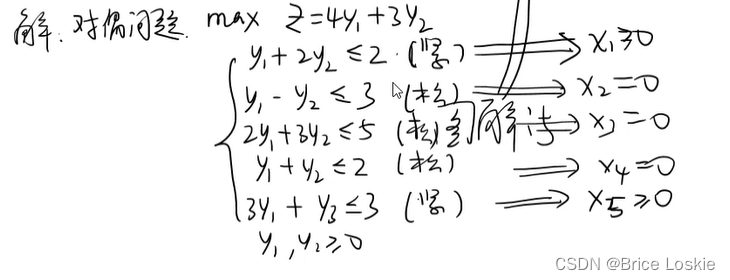
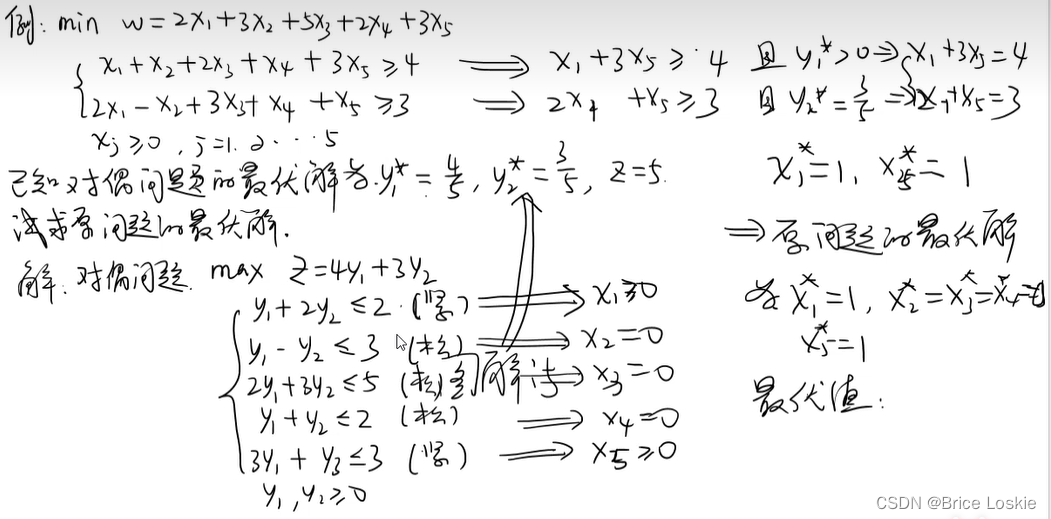
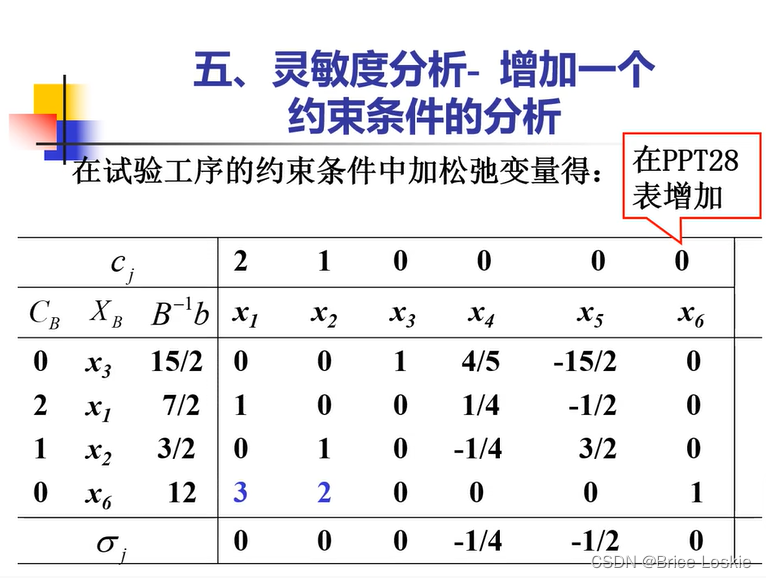
 考试前多了看ppt上的题，这里直接给的思想，我们需要给出增加算法

灵敏性分析专栏：之后补加